基于面积型Froude数的浑河流域河相系数计算及沿程关系探讨

习丽丽

(辽宁省沈阳水文局，辽宁 沈阳 110043)

河床演变与河道形态关系密切，河相系数是分析河道演变及其稳定的关键参数，对于河道整治和规划具有重要的参考意义[1]。当前对于河相系数的计算主要是结合河道地形数据，通常采用水深型Froude数进行河相系数的计算[2- 5]，但是水深型Froude数很难对河道纵向和横向稳定系数进行分析，对河相系数的总体把握较为困难。近些年来，一种考虑水面面积的面积型Froude数在河道整治工程中得到应用[6- 10]，该方法对河道形态变化可以较为准确的把握，但在河相系数分析中还应用较少。为此本文引入面积型Froude数，以浑河为研究实例，分析面积型Froude数在河相系数计算的适用性，并对河相系数沿程分布进行探讨。研究成果对于河道整治和规划具有重要的参考意义。

1 河相系数计算方法

面积型Froude数首先通过计算河道纵向和横向稳定系数来计算河床的综合稳定指标，其中横向稳定系数计算方程为：

(1)

式中，φb—横向稳定系数；Q—平摊流量，m3/s；B—主槽的宽度，m；J—河床比降，‰。

φb计算值越大，表明其河岸的稳定性越高，反之则越弱。

在横向系数计算的基础上，对纵向系数进行计算，计算方程为：

(2)

式中，φh′—纵向系数；h—纵向水深，m；D—河床床砂粒径，mm，该参数表征为河床稳定性的特征值。

在横向和纵向稳定系数计算的基础上，对综合稳定系数进行计算，计算方程为：

(3)

式中，φ—综合稳定系数；其他变量同上述方程中的变量含义。

在综合稳定系数计算的基础上，结合纵向和横向的变化特征，构建河道综合稳定性指标，计算方程为：

(4)

式中，Zw—河道综合稳定指标；X*、Y*—横向和纵向变化特征向量；rs—河床粗砂粒径，mm；r—河床细砂粒径，mm。D50—河床床砂50%的粒径，mm。

在各河床稳定指标计算的基础上，对面积Froude数进行计算，计算方程为：

(5)

式中，FrA—面积Froude数；g—河床特性参数值。

2 研究实例

2.1 浑河概况

以浑河流域为研究实例，浑河是辽宁中东部最大的河流，河流总长为495km，流域总的面积为13444km2。浑河流域流经抚顺、沈阳、辽阳、鞍山等主要城市，干流主要大型水库为大伙房水库；大伙房水库以上为山区型河流，河谷较为狭窄，河流摆动幅度较小；大伙房水库以下到长大线的铁桥，河流主要为低山区型河流，河流逐步开阔，河宽逐步增加，这一区间河段的平均比降为0.85‰；从长大线铁桥后进入河道平原区，这一部分河流长度为174km，河床的比降0.41‰～0.11‰，河床的主要质地为粗砂和细砂。

2.2 河段综合稳定性指标计算结果

选取浑河20个典型河段，结合各河段特性数据，对河段纵向、横向稳定系数进行分析；在此基础上，对各河段的综合稳定性指标进行计算，结果见表1，并对各河段纵向、横向稳定系数和综合稳定指标的相关性进行分析，结果如图1所示。

从表1中可看出，浑河各河段纵向和横向稳定系数变化差异性较大，各河段的纵向稳定系数从0.21～6.48之间变化，纵向稳定系数主要表征河道泥沙运动的稳定强弱，纵向稳定系数越大，表明该河段泥沙运动强度越大；纵向稳定系数越低，表明其河段泥沙稳定性越低。从纵向稳定系数可看出，浑河大伙房水库以上河段主要为山丘型河流，其纵向稳定系数较大，河段泥沙运动强度较大；而在大伙房至长大线铁桥河段及该河段以下主要为低山丘型及平原型河段，这些河段的纵向稳定系数在0.21～1.78之间，河段泥沙运动强度总体较弱。从横向稳定系数可看出，浑河流域各河段的横向稳定系数总体在0.06～0.33之间变化，大伙房水库以上河段的横向稳定系数在0.06～0.19之间，稳定系数较低，河床稳定性较弱；而大伙房至长大线铁桥河段及该河段以下横向稳定性系数在0.19～0.33之间，河床稳定性较高。从各河段综合稳定性指标可看出，浑河各河段的综合稳定性指标空间分布差异性较大，受到河道特性综合因素影响，使得其综合稳定性指标变化较大。从横向、纵向稳定系数和综合稳定系数相关性分析结果可看出，纵向稳定性系数和综合稳定性指标相关度较高，因此综合稳定性指标受到纵向河床变化影响较大。

表1 各河段综合稳定性指标计算结果

图1 河道纵向、横向稳定系数与综合稳定指标相关性分析结果

2.3 基于面积型Froude数的河相系数分析

结合面积型Froude数对各河段的河相系数进行计算，并对河型进行划分，分析结果见表2，此外分析河相系数和水深型以及面积型Froude数的分布关系，如图2所示。

表2 基于面积型Froude数的河相系数分析结果

图2 各类型河道Froude数和河相系数的关系分析结果

从表2中可看出，采用面积型Froude数的河相系数计算结果可对各河段的实际类型进行划分。当FrA<0.070时，主要为游荡型河段，而0.0700.085时，主要为弯曲型河段。从表中还可看出，面积型Froude数相比于水深型Froude数更适合于河相系数的计算，对于同一类型河道而言其计算结果和综合稳定指标Zw的相关度较高。河段FrA和Zw越小，其河道的稳定性越低，河宽约为散乱。从图3中可看出，各河道类型的面积型Froude数与河相系数的散点关系更为集中，而水深型Froude数与河相系数散点关系更为散乱。河相系数主要为河宽与水深的关系，通过图3可建立不同河段类型的拟合方程，结合河段Froude数计算结果，可以探讨不同河型下整治流量和对应宽度的范围。

2.4 年代Froude数的河相系数相关性分析

为分析浑河流域河相系数的演变特征，结合选取的20个典型河段，对各年代际两种类型Froude数和河相系数的均值进行相关性分析，结果如图3所示。

图3 不同年代际各类型Froude数和河相系数演变关系分析结果

图3为选取典型河段各代际河相系数与各类型Froude数的均值演变分析结果，从图3中可看出，各年代际面积型Froude数与河相系数散点较为集中，而水深型Froude数与河相系数相关性的散点较为散乱，同一河相系数下，面积型Froude数要大于水深型Froude数，这点也可看出，面积型Froude数更适用于河相系数的计算。从各年代际变化可看出，1990—1999年河相系数与Froude数相关性总体较低，这一时期河流摆动幅度较大，演变程度较大，而从2000年开始，由于加大河道的综合治理，2000—2009年和河相系数与Froude数的散乱度降低，可以看出，河流演变程度减小，而进入2010年后，浑河总体演变较为稳定，2010—2018年河相系数与Froude数的散乱度集中度增强，河势的稳定性增强。

2.5 不同流量下河相系数沿程关系探讨

为探讨河相系数沿程分布，针对不同流量下的河相系数沿程分布进行分析，结果如图4所示。

从图4中可看出，随着流量的增加，河相系数和流量总体呈现指数变化关系，河相系数的散点集中度不断增强，表明在同一流量下，随着沿程距离增加，河相系数不断加大。这主要是因为随着沿程距离增加，河道宽度有所增加，而河道宽度是河相系数的重要指标，因此河相系数增加。从各流量下河相系数和和沿程距离的相关系数可看出，随着流量增加，相关性逐渐增加。

2.6 不同流量下沿程河相系数拟合方程分析

结合不同流量下河相系数的相关方程，建立不同流量下沿程河相系数拟合方程，并结合实测数据对拟合方程的待定系数误差进行分析，见表3，此外，定量分析流量与两个参数之间的相关性，结果如图5所示。

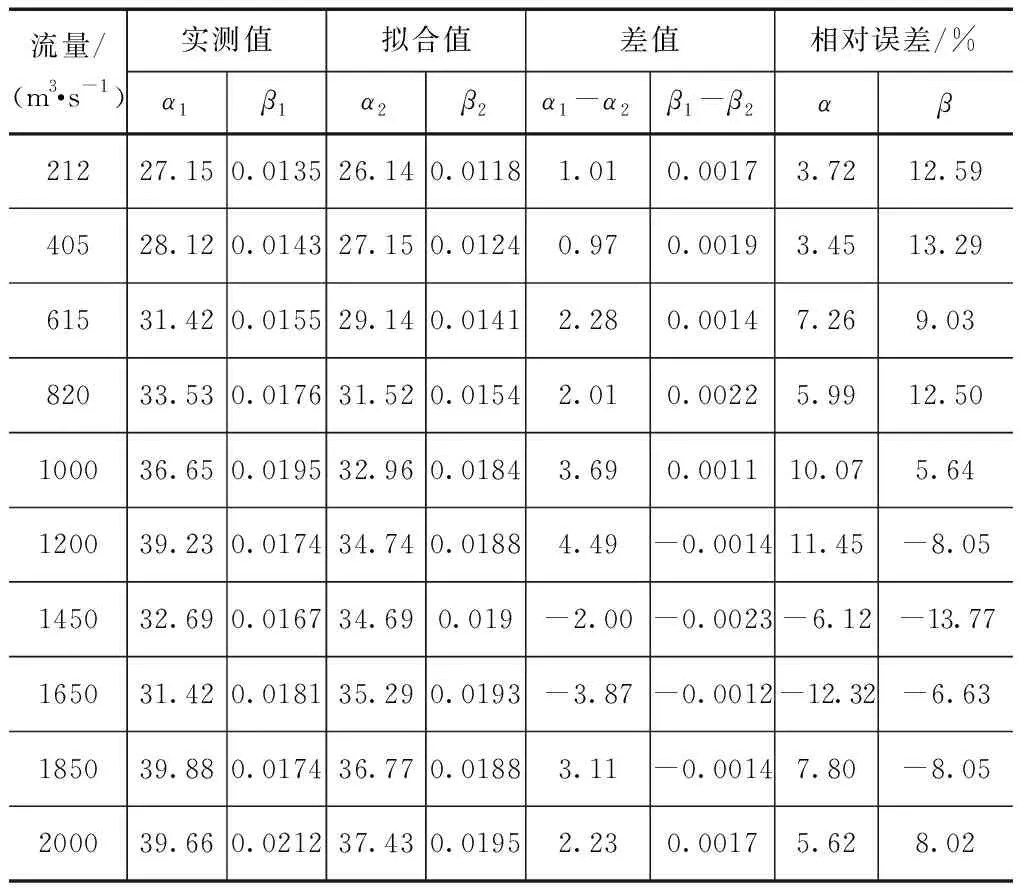
表3 各流量下河相关系待定系数及其误差分析结果

从实测值和计算值的误差分析结果可看出，两个参数的差值和相对误差都在误差许可的范围之内，两个参数的相对误差均在15%以内，差值误差在±5.0之间，各流量下的河相系数沿程分布的拟合方程可以用来推求不同类型河道整治宽度和流量的范围。从河道流量与拟合方程两参数的相关性分析结果可看出，流量与拟合方程待定系数的相关系数均较高，呈现强相关性。

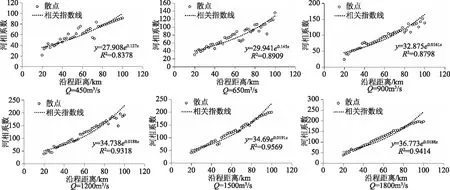
图4 不同流量下河相系数沿程分布结果

图5 河道流量与两个参数之间的相关性分析结果

3 结论

(1)相比于水深型Froude数，面积型Froude数在河相系数计算上适用性更强，在不同河型河相系数计算上具有推广价值。

(2)浑河大伙房水库以上河段综合稳定性较低，综合稳定指标在1.75～6.52之间，且主要以弯曲型河流为主，而长大线铁桥河段综合稳定系数在6.52～16.38之间，主要为分叉型和游荡型河流。对于同一类型河道，河段FrA和Zw越小，其河道的稳定性越低，河宽约为散乱。

(3)本文重点探讨了不同流量初始条件下河相系数沿程分布，对于流量沿程变化下河相系数变化还未进行研究，在以后还需要对流量沿程变化对河相系数影响进行深入研究。