远程操控飞行器自适应神经网络观测器设计

许红羊，李宏君，凡永华，闫 杰

(1. 西北工业大学航天学院，西安 710072；2. 西安航天动力研究所，西安 710100)

0 引 言

远程操控无人作战飞行器(Remotely piloted vehicle,RPV)可以同时发挥飞行员战场感知能力好、决策能力强的指挥优势和无人机战术实现灵活、持续作战能力强且全寿命周期成本低的性能优势，同时可以有效减少人员伤亡是未来空中作战的主要发展方向[1-2]。远程操控飞行器在实际作战中，飞行员可以在有人机或地面控制站通过人-机界面显示的飞行器状态按照作战任务实时对飞行器进行远程驾驶[3-4]。由于RPV具有飞行包线范围大、模型高度非线性以及参数不确定等特点，此外在实际工程应用中，对于远程操控人员而言，其对RPV的操控效果不仅与RPV本身的气动特性有关还与RPV飞行控制系统的响应特性和舵机等执行机构的非线性特性相关，因此，充分考虑远程操控飞行器动力学和控制系统特性，建立合理的、精确的控制系统模型是开展RPV远程操控系统设计的关键[5-6]。

目前，国内外学者针对RPV的远程操控问题做了大量的研究工作，大部分研究是基于确定性模型的[7-9]。文献[10]分析了远程操控无人机较大的数据链路延迟对操作品质的影响，针对无人机远程操控存在时滞的问题，提出了一种基于线性时不变模型的状态预测方法，有效的减轻了飞行员的工作负荷提高了Cooper-Harper评级。然而，由于系统存在未建模动态和附加扰动，整体的性能未得到改善。文献[11]同样以确定性线性模型为基础，采用基于模型的预测方法提出了三种远程操控飞行器的状态预测算法，显然这些方法只适用于理想模型假设的条件下。文献[12]在无人机远程操控技术研究中考虑了噪声的影响建立了无人机的线性离散模型。文献[13]针对具有参数不确定性的系统，采用Lyapunov-Krasovskii方法设计了模型参考自适应控制器，有效的解决了系统存在输入延迟的问题。以上的研究在远程操控飞行器延迟预测和鲁棒控制等方面均取得了很好的效果，但它们都假设模型已知或在建模过程中都没有考虑到远程操控飞行器飞行控制系统本身的响应特性和舵机等执行机构的非线性特性对RPV闭环系统的影响。

目前针对模型存在非线性、未建模动态和附加扰动等问题，智能控制算法得到了广泛的应用[14-17]。径向基函数(RBF)神经网络由于具有良好的泛化能力，能在一个紧凑集和任意精度下逼近任何非线性函数，是解决具有未建模动态的非线性系统建模的有效途径[18-19]。文献[20-23]针对典型的非线性系统采用神经网络方法有效的解决了模型的不确定性，并通过Lyapunov理论证明了系统的稳定性。

本文针对远程操控飞行器气动特性复杂、气动-控制强相关，无法精确建模的问题，提出了一种自适应神经网络状态观测器设计方法实现对远程操控飞行器控制系统模型的在线辨识。考虑到远程操控飞行器动力学和飞行器控制系统的不确定性，将飞行器的动力学环节与自动驾驶仪构成的闭环回路作为一个整体建立了远程操控飞行器控制系统的非线性模型。针对模型中存在未建模动态的问题，采用神经网络算法对非线性动力学模型进行在线辨识，并引入鲁棒项对扰动进行抑制。设计自适应律对神经网络的权值进行实时调整，保证了系统的稳定性，并基于Lyapunov理论证明了观测器的估计误差是最终一致有界的。仿真结果表明，所设计的观测器能够保证远程操控飞行器在存在未建模动态和附加扰动的情况下具有良好的估计性能。

1 模型描述和问题提出

1.1 模型描述

远程操控飞行器纵向通道动力学模型如下：

(1)

式中：H,V,α,ϑ和q分别表示飞行器的高度、速度、攻角、俯仰角和俯仰角速度，Vy和ny分别为法向速度和法向过载，Iyy为俯仰转动惯量，m为质量，g为重力加速度，Myy为俯仰力矩，其符合定义为正的升降舵偏角产生负力矩，L和D分别为飞行器的升力和阻力。L,D和Myy的具体表达式如下：

(2)

(3)

式中：Ma为马赫数，ρ0和H0是标准大气密度以及相应的高度，1/Hs是大气密度的衰减律。δe为升降舵偏角。

1.2 问题提出

远程操控飞行器在执行作战任务时，控制站与飞行器通过数据链路进行远程通信，飞行员根据人-机界面显示的飞行器飞行参数，按照战术任务形成操控指令。飞行器实时接收飞行员的操控指令，飞行器的飞行控制系统按照预定的控制算法生成舵机控制指令，舵机按照指令偏转舵偏，进而控制飞行器按照飞行员的意图飞行。因此对于远程操控人员，在设计和操控RPV时不仅要考虑飞行器本身的气动特性和动力学特性还应将飞行器的控制系统和执行机构一并考虑在内，应该将RPV的气动特性和控制系统作为一个整体建立气动-控制闭环模型。RPV远程操控示意图如图1所示。

从图1可以看出，远程操控飞行器的飞行控制系统主要包括：RPV控制器、执行机构和RPV动力学三个部分。考虑到实际工程中执行作战任务时，RPV控制器通常采用法向过载控制系统实现战术机动，因此本文对采用法向过载控制器的RPV对象进行建模分析。其模型主要存在以下三个难点：1)控制系统的响应特性随着飞行包线和作战任务的不同具有很大的变化，很难用模型精确描述；2)执行机构舵机系统存在死区和舵机饱和等非线性约束，使模型存在非线性；3)RPV飞行器气动特性复杂，战术机动过程中通道间耦合较大，模型不确定性强。综上所述，RPV飞行器法向过载控制系统从过载指令到过载响应间的动态模型具有非线性和不确定性的特点，考虑附加扰动的影响，确定如下模型形式：

(4)

注1. 本文的研究目标为：设计一种自适应神经网络观测器，在线辨识模型(4)中的未知非线性函数f(x)和g(x)，对系统状态进行估计，从而使得状态估计误差是最终一致有界的。

2 自适应神经网络观测器设计

2.1 RBF神经网络

采用RBF网络，可实现未知非线性函数λ(ξ)的逼近，RBF网络算法为：

λ(ξ)=W*TΦ(ξ)+ε(ξ)

(5)

(6)

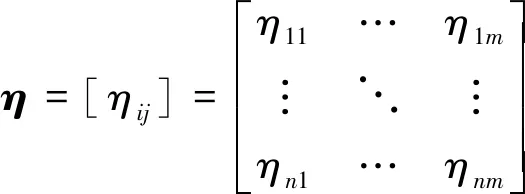
采用RBF神经网络逼近未知函数λ，网络输入取ξi，则RBF网络的输出为：

(7)

2.2 自适应RBF网络观测器设计

针对式(4)，可设计如下观测器：

(8)

(9)

(10)

则可得出如下的输出误差传递函数方程：

(11)

式中：s表示微分算子d/dt，线性传递函数H(s)=CT(sI-A+ΓCT)-1b，且H(s)为严格正实。

引理1[18]. 如果系数矩阵A满足Hurwitz条件，且有理函数H(s)=CT(sI-A)-1b是严格正实的，那么存在一个正定对称矩阵P使得：

ATP+PA=-Q,Pb=C

(12)

式中：Q为正定对称矩阵。

引理2[18]. 考虑如下形式的线性时不变系统：

(13)

式中：x(t)∈Rn,u(t)∈Rm，矩阵A∈Rn×n,B∈Rn×m，则由文献[18]可得，对于式(13)中x(t)的任意解均满足：

(14)

式中：k1随着x0指数衰减到零，k2是一个正常数，其值取决于矩阵A的特征值。

在观测器式(8)中，f(x)和g(x)均采用RBF神经网络进行估计。由2.1小节可知，未知连续非线性函数可采用理想权值W*和足够数量的基函数Φ(x)组成的神经网络表示。即：

(15)

式中：x∈Qx⊂Rp为网络的输入向量，p是神经网络输入的维数，ε1(x)和ε2(x)是神经网络的逼近误差，ε1,N和ε2,N为逼近误差的上界。

采用神经网络逼近f(x)和g(x)，表示为：

(16)

(17)

则式(17)可写为

(18)

且wi(t)为有界的，即：

式中：β1,β2>0。

可设计如下的神经网络观测器：

(19)

式中：v1和v2为鲁棒项。进一步可得估计误差为：

(20)

由式(20)可得，输出误差的传递函数方程可表示为：

(21)

式中：H(s)为由(A-ΓCT,b,C)定义的已知传递函数，且极点均在复平面的左半平面内。进一步将式(21)表示为如下形式：

(22)

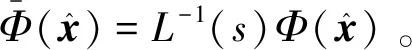
(23)

注3. 式(22)的每一项都需要经过L-1(s)滤波。这个误差方程仅用作分析。

给出式(22)的状态空间实现如下：

(24)

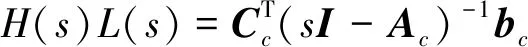
神经网络观测器的鲁棒项由以下形式给出：

(25)

式中：D1≥β1σM；D2≥β2σMud；σM=σmax[L-1(s)]；σmax[·]为最大奇异值。

设计神经网络自适应律为：

(26)

RPV自适应神经网络观测器结构如图2所示。

2.3 稳定性分析

证. 考虑如下Lyapunov函数：

(27)

式中：P=PT>0，由于H(s)L(s)是严格正实，则存在P=PT>0使得

(28)

式中：Q=QT>0。对函数V求导，结合式(28)有：

(29)

考虑式(25)、式(26)有：

(30)

由于

则有：

(31)

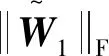
(32)

或

(33)

整理式(20)为

(34)

式中：

w2+ε2)u+d+v1+v2。

(35)

进一步可得，式(34)的解为

(36)

取

Ξ(t,0)=exp((A-ΓCT)t)，Ξ(t,τ)=exp((A-ΓCT)t-(A-ΓCT)τ)，

则上述方程可改写为：

(37)

由于

exp((A-ΓCT)t-(A-ΓCT)τ)=

exp(A(t-τ))exp(-ΓCT(t-τ))=

m0exp(-α(t-τ))

式中：m0=exp(A(t-τ)),α=ΓCT。则有，Ξ(t,τ)=m0exp(-α(t-τ));m0exp(-α(t-τ))是Ξ(t,τ)的上界，m0和α均为正常数。

根据引理2和式(34)可得：

(38)

式中：

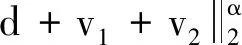
定义c=w1+ε1+(w2+ε2)u+d+v1+v2，则：

(39)

由于：

(40)

同理可得

(41)

(42)

将式(42)代入式(38)中，可得

(43)

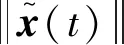
3 仿真校验

为了验证本文提出的自适应RBF观测器的有效性和鲁棒性，基于前述的模型进行了数字仿真。仿真的初始条件为：飞行高度H0=8000 m，飞行速度V0=246 m/s，法向速度Vy0=0 m/s，攻角α0=0 rad，俯仰角ϑ0=0 rad，俯仰角速度q0=0 rad/s，法向过载ny0=0。

文中以工程上常用的飞行器法向过载三回路自动驾驶仪为例，作为远程操控飞行器研究对象，通过本文提出的方法对控制系统输入输出模型进行逼近，对系统状态进行估计。仿真所用的RPV法向过载控制律如下：

(44)

式中：kq,kα和kny为控制系统的增益，分别取值为kq=-0.3738,kα=4.1729和kny=0.15确保控制系统具有良好的响应特性。

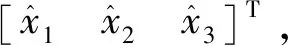
仿真中控制参数不变，首先在标称大气的情况下，采用本文提出的方法进行仿真校验方法的有效性。此外，在有气动偏差、舵机模型非线性和外界扰动的情况下进行仿真，校验了该方法的鲁棒性。

3.1 有效性仿真

在标称情况下进行仿真校验，仿真结果如图3～6所示。图3给出了RPV法向过载控制系统的响应特性，从图中可以看出法向过载响应曲线光滑，能够快速跟踪过载指令。图4中的(a)～(c)分别为RPV法向过载控制系统输出的法向过载、法向速度和高度的实际值和自适应神经网络观测器输出的相应状态的估计值。图5为估计误差。从图4和图5可以看出，在存在初始状态偏差的情况下，法向过载估计值1.5 s快速收敛到实际值，法向速度和高度的收敛速度分别为0.8 s和0.2 s，且随后的估计误差收敛到零。图6给出了神经网络输出的非线性函数f(x)和g(x)的逼近值。从图中可以看出，逼近曲线光滑且收敛。

3.2 鲁棒性仿真

为了校验本文所提出的观测器的鲁棒性，考虑在有气动偏差、舵机模型死区和外界扰动的情况下进行仿真。引入+30%的气动力矩偏差和+10%的气动力偏差，舵机死区选为±0.2°，外界扰动d(t)=0.1cos(0.7t)，仿真结果如图7～10所示。

从图7法向过载响应、图8(a)法向过载状态估计曲线和图9(a)的估计误差曲线可以看出，在存在气动偏差、舵机死区和外界扰动的情况下，法向过载估计值能够快速收敛至实际值，估计误差基本为零，在法向过载指令过零时，由于舵机死区的影响，过载响应出现0.1 s保持不变的现象，过载估计值与过载实际值吻合较好，估计误差小于0.01。从图8(b)和图9(b)可以看出法向速度估计误差小于0.004 m/s，从图8(c)和图9(c)可以看出高度估计值快速收敛至实际值，在存在气动偏差、舵机死区和外界扰动的情况下估计误差仍然快速收敛至零。图10给出了神经网络输出的非线性函数f(x)和g(x)的逼近值。从图中可以看出，逼近曲线光滑且收敛。通过仿真校验，证明了本文所提方法的有效性和鲁棒性。

4 结 论

本文针对无人飞行器远程操控系统设计时，无法精确建立远程操控飞行器控制系统模型的问题，提出了一种基于自适应神经网络的非线性模型逼近方法，实现了对远程操控飞行器动力学和控制系统闭环特性的估计。将飞行器的动力学环节与自动驾驶仪构成的闭环回路作为一个整体建立了远程操控飞行器控制系统的非线性模型。针对模型中存在未建模动态的问题，采用神经网络算法对非线性动力学模型进行在线辨识，并引入鲁棒项对附加扰动进行抑制。设计自适应律对神经网络的权值进行实时调整，保证了系统的稳定性，并基于Lyapunov理论证明了观测器的估计误差是最终一致有界的。仿真表明所设计的非线性观测器，可以保证系统在存在气动偏差、舵机非线性和外界扰动的情况下对远程操控飞行器状态具有良好的估计性能。