质量矩导弹固定时间二阶滑模控制方法

赵金龙，郭建国，周 军

(西北工业大学精确制导与控制研究所，西安 710072)

0 引 言

现代战争模式的多样化不断对导弹武器的机动能力提出新的要求，质量矩控制技术由于其控制效率高、气动外形完整等优点引起了极大关注，并相继研究应用于再入弹头、滑翔飞行器、拦截弹、以及水下航行器等。质量矩控制的原理是通过移动飞行器内部的活动质量块来改变系统质心位置，形成气动力相对于质心的偏移，进而产生控制力矩，实现对飞行器姿态的控制。内部质量块的移动使得导弹各通道间存在强烈的动力学耦合，给控制系统的设计带来了极大的困难[1-3]。

滑模控制是一种具有强鲁棒特性的非线性控制方法。滑模控制的闭环系统收敛过程可分为趋近阶段和滑模运动阶段，传统的设计方法中趋近阶段系统收敛时间有限，但滑模运动过程的收敛时间则趋近于无穷。为了实现滑模运动过程的有限时间收敛，终端滑模、非奇异终端滑模等设计方法相继提出，但系统的收敛时间与状态初值严格相关，无法对其进行主动调节以实现固定时间控制[4-8]。因此，学者们提出了固定时间收敛的概念，使得系统收敛时间不依赖于状态初值，并先后设计了固定时间收敛的终端滑模、非奇异终端滑模、二阶滑模等方法[9-14]。固定时间收敛的控制方法还进一步研究应用于高超声速导弹[15-16]、拦截弹[17]、再入飞行器[18]、航天器[19-20]等各类飞行器。

本文针对三轴稳定的质量矩导弹，基于动态系统零点配置原理提出了一种快速固定时间二阶滑模控制方法，并通过分析闭环系统状态变量的收敛过程对收敛时间上界进行了估计，仿真结果表明该方法能够获得更高的动态特性，满足质量矩导弹姿态控制需求。

1 质量矩导弹数学模型

本文所针对的三轴稳定质量矩导弹由弹体和分别沿弹体y轴、z轴方向运动的双活动质量块p，r组成，弹体质心位置为B*，系统总质心位置为S*，内部结构如图1所示。

导弹分别在俯仰和滚转通道进行质量矩姿态控制，动力学建模将活动质量块视为质点，不考虑其转动特性，且忽略地球自转的影响。

设弹体B、活动质量块p、r的质量分别为mB,mp,mr，则系统总质量ms和质量比μp，μr可表示为

(1)

弹体相对发射坐标系的角速度在弹体坐标系下可表示为

(2)

双活动质量块在弹体坐标系下的位置分别为

(3)

式中：lp0，lr0分别为俯仰、滚转通道质量块滑轨中心在弹体坐标系x轴坐标；δy，δz分别为俯仰、滚转通道质量块在滑轨内的位置坐标。

根据动量矩定理，可得质量矩导弹绕质心转动动力学方程为

(4)

式中：J为弹体转动惯量矩阵,F为弹体所受气动力矢量,M为弹体气动力矩矢量,ΔJ为系统附加惯量，可表示为

ΔJ=-mp((1-μp)(rp×)-μr(rr×))(rp×)-

mr((1-μr)(rr×)-μp(rp×))(rr×)

(5)

质量块的运动将引起飞行器惯性主轴偏移，从而产生附加转动惯量；而质量块运动引起系统质心的变化则会产生通道间耦合力矩，包括附加气动力矩、附加惯性力矩、以及附加哥氏力矩等。强烈的通道间耦合将显著增强控制系统的设计难度。

2 固定时间滑模控制律设计

2.1 固定时间系统的零点配置

考虑如下的动态系统

(6)

式中：λ>0,p>0,q>0, sgn(x)为符号函数。

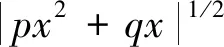
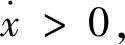
2) 初始状态-q/p0，系统轨迹将直接收敛至平衡点x=0。

虽然x=0为系统(6)的唯一平衡点，但系统其它的零点位置将直接影响系统的运动轨迹和收敛速度，因此，可通过设计系统闭环系统零点调节动态品质。首先分析上述系统的固定时间收敛特性。

定理1. 对于闭环系统(6)，设系统初始状态满足|x0|

(7)

证.假设系统初始状态x0>0，则px2+qx≥0，系统(6)可写为

(8)

式(8)进一步可写为

(9)

采用积分方法可得系统状态从初始值到平衡点得到收敛时间为

(10)

第二种情况，假设初始状态x0>-q/p，则系统状态将直接收敛至平衡点，采用上文的方法同样可得式(10)所示收敛时间。

2.2 固定时间二阶滑模控制律

对于滑模动态系统

(11)

式中：s为滑模变量，a(t,x)为系统状态函数，b(t,x)为控制增益函数，u为控制变量。

本文基于动态系统(6)的收敛特性，提出一种新型Super-twisting滑模控制律如下：

(12)

式中：λ,p,q,ρ>0,m>1, 0

引理1[21-23]. 考虑标量微分方程

(13)

式中：λ,μ>0,m>1,n<1。

该方程具有一个与初值z(0)无关的有限调节时间T0，其上界可表示为：

(14)

定理2. 对于滑模动态系统(11)，如果采用式(12)所示控制律，则滑模变量将在固定时间内一致收敛至平衡点，收敛时间上界可表示为：

(15)

式中：K为状态初值的上界。

证. 将控制律(12)代入系统(11)，可得闭环滑模动态方程：

(16)

式中：t0为初始时间，s0,v0为系统初始状态。可见，相平面内原点(s,v)=(0,0)为闭环系统唯一平衡点。

采用与文献[24-26]类似的证明方法，根据系统初始状态符号的不同情况估算状态收敛时间。

首先考虑初始状态符号相反的情况，sgn(s0)=-sgn(v0)，则式(16)中第一个方程可写为：

(17)

对于任意的实数a和b有不等式：

(18)

因此，式(17)可写成：

(19)

根据引理1可知，滑模变量s将在固定时间内到达零点，到达时间T1上界为：

(20)

在时间区间t∈[t0,t0+T1]内，滑模变量s的符号与v相反。从式(16)可以看出，|v|将以恒定的速度ρ增大，则在t0+T1时刻，变量|v(T1)|的上界可表示为：

|v(T1)|≤K+ρT1

(21)

当时间t>t0+T1时，滑模变量s的符号将与变量v一致，|s|和|v|将同时收敛至平衡点。由于|v|的收敛速度为恒值ρ，因此，收敛时间T2的上界可估算为

(22)

则滑模变量s和变量v收敛至平衡点的总时间Tf 1的上界可表示为

(23)

如果滑模变量s的符号与变量v相同，那么|s|和|v|将同时减小并收敛至平衡点。考虑到变量v的收敛速度为恒值ρ，因此，总的收敛时间上界可表示为

(24)

综合以上两种情况，可得闭环系统(16)的固定收敛时间上界为

Tf=max{Tf 1,Tf 2}=Tf 1

(25)

3 仿真分析

假设导弹壳体质量mB=10 kg，滑块质量mp=mr=1 kg，质量块最大行程为32 mm，最大速度0.1 m/s。纵向通道跟踪系统过载指令，滚转通道进行滚转角稳定控制，并设初始滚转角为3°，仿真结果如图2～5所示。

图2～3分别为纵向过载指令响应和弹体y轴质量块运动曲线，可以看出，活动质量块最大位移量0.03 m便可建立最大过载1，控制效率较高，系统收敛速度快。图4～5分别为弹体滚转角曲线和z轴质量块运动曲线，可见弹体滚转角快速收敛至0，质量块位移接近最大行程，控制效果比较理想。

4 结 论

针对三轴稳定的双滑块质量矩导弹，本文首先建立了具有完整耦合动力学特征的质量矩导弹姿态动力学模型；其次，基于典型动态系统进行零点配置原理分析和收敛时间估计；在此基础上，提出动态过程可调节的固定时间二阶滑模控制方法，并对系统收敛时间的上界进行估计；最后，针对质量矩导弹的仿真校验了设计方法的有效性。