微小卫星多约束姿态机动规划方法

冯振欣，郭建国，周 军

(1. 西北工业大学航天学院，西安 710072；2. 微小卫星技术及应用国家地方联合工程实验室，西安 710072)

0 引 言

微小卫星具有研制周期短、成本低、响应快速、易于组网应用的显著特点，目前已经在对地遥感、新技术验证、深空探测等领域展现出巨大的应用潜力。典型代表有美国Planet Labs的鸽群卫星对地遥感星座、Marcos火星立方星一号等。然而，微小卫星自主控制技术依然面临诸多挑战。

由于星上光学传感器(如星敏感器)测量性能受杂光影响很大，为抑制杂光保证光学传感器正常工作，其光轴与地球、太阳的夹角必须满足一定的条件；而对于一定作用范围的高增益天线来说，则需调整姿态保证天线对地通信，这就对卫星姿态指向提出了约束要求。传统大卫星体积大安装限制少，可以通过优化光学传感器和天线安装布局满足指向约束要求。但是对于体积、功耗都严格限制的微小卫星来说，由于安装面有限，仅通过布局优化已经难以有效解决。因此，采用姿态机动规划方法成为微小卫星满足指向约束要求的必然选择。

对于卫星姿态机动规划问题，目前主要有两种思路。一种思路是采用在线规划的方法，即通过优化方法得到满足指向、能量约束的轨迹。如文献[1]采用半定规划方法解决卫星多约束下的最优姿态控制问题；武长青等[2]将卫星动力学约束、有界约束和姿态指向约束问题归纳为非凸二次约束二次规划问题，并引入评价函数迭代规划获取全局姿态优化路径；程小军等[3]基于凸优化方法提出了考虑输入有界的姿态机动预测控制算法。文献[4-5]基于离散A*算法搜索满足约束的姿态机动轨迹。文献[6]则提出了一种考虑时间因素的改进快速搜索随机树姿态规划方法。这一类方法虽然能够获取满足约束的轨迹，但计算量较大，对于星上处理能力要求较高。另一种思路是确定性解析方法。目前主流方法是势函数方法[7-9]，其基本思想是当姿态接近禁止指向区域时产生排斥力，而期望指向对机动姿态产生吸引力，从而保证姿态轨迹既满足禁止指向约束又能机动到期望姿态。该类方法计算量小，适合微小卫星在轨自主控制。此外，文献[10-12]还分别针对卫星控制受限问题、角速率约束问题、执行机构故障问题提出了相应的控制方案。

结合上述分析，本文基于对数型势函数和障碍Lyapunov函数方法设计了微小卫星姿态控制器，解决了微小卫星禁止指向约束和强制指向约束多类型的指向约束和角速率约束问题。同时，针对外界干扰力矩，引入自适应干扰估计律降低不确定性对控制系统的影响。与现有方法相比，本文方法计算量小，同时考虑了多种姿态指向约束和角速率约束，非常适合于星上处理，能够满足未来微小卫星多任务快速机动的需求。最后，通过数值仿真校验了本文设计方法的有效性。

1 微小卫星控制模型及相关引理

1.1 微小卫星动力学与运动学模型

卫星的四元数运动学模型如下

(1)

卫星动力学方程如下

(2)

考虑到陀螺的量程限制以及传感器测量要求，卫星角速率被限制在一定范围之内。

(3)

式中：i=1,2,3;ωmax为允许的最大角速率。

同时，微小卫星执行机构一般采用飞轮与磁力矩器，控制力矩幅值有限，需满足

(4)

式中：i=1,2,3;umax为允许的最大控制力矩。

1.2 指向约束问题描述及相关引理

如图1所示，向量vs,ve分别表示卫星轨道系中卫星与太阳、卫星与地心连线的单位矢量。向量vob,vab分别表示卫星本体系下光学传感器的光轴指向、通信天线指向的单位向量。θ为向量vob与vs之间的夹角，θ′为向量vab与ve之间夹角。

由单位向量的内积运算法则，满足如下关系

(5)

为保证光学传感器避免强光照射以及天线对地正常工作，定义姿态禁止指向最小约束角θF和强制指向最大允许角θM满足如下关系

(6)

不失一般性，θF,θM均小于π，因此

(7)

由四元数运算关系可得轨道系中的光学传感器向量v′ob和天线轴向向量v′ab分别为

v′ob=vob-2(qTq)vob+2(qTvob)q-2q0(vob×q)

(8)

v′ab=vab-2(qTq)vab+2(qTvab)q-2q0(vab×q)

(9)

通过代数运算,进一步可得

(10)

(11)

式中:

禁止指向集合.为避免强光天体进入卫星光学传感器视场，需满足如下集合：

(12)

强制指向集合.对于通信天线而言，需要保证地球始终处于天线作用的视场内，则需满足

(13)

引理1. 对于对数型势函数:

(14)

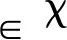
1)VF(Qd)=0；

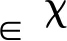
证明详见文献[7]。

同理，根据卫星对地通信的天线向量与星-地连线的几何关系可设计如下势函数：

(15)

类似地，可以证明式(13)同样满足引理1条件。

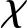
(16)

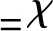
V→∞,当|x|→kc

(17)

(18)

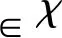
(19)

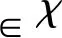
2 控制器设计

这一部分针对微小卫星姿态多重指向约束和角速率约束设计控制器，并利用Lyapunov稳定性理论对控制系统稳定性进行分析和证明。

2.1 约束控制律设计

式(14)的梯度可计算为

(20)

式(15)的梯度可计算为

(21)

对于干扰力矩di,i=1,2,3，设计非线性自适应律

(22)

结合式(14)～(15)和障碍Lyapunov函数,设计Lyapunov函数如下

(23)

(24)

(25)

将式(1)～(2)、 式(20)～(22)代入式(25),可得

(26)

式中:Vec(·)表示四元数(·)中矢量部分组成的列向量，(·)*表示(·)的共轭四元数。

因此，控制律设计为

(27)

2.2 稳定性分析

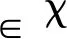
证. 将式(27)代入式(26)经整理后可得

(28)

由Young不等式可知

(29)

(30)

将式(29)～(30)代入式(28)可得

(31)

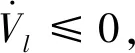
3 仿真校验

针对某太阳同步轨道微小卫星，轨道倾角为98.195°，升交点赤经135°，轨道高度500 km，卫星转动惯量J=diag(0.0065,0.0418,0.0418)kg·m2。假设光学传感器沿卫星本体系Y轴安装，光轴指向向量为(0, 1, 0)；通信天线在卫星本体系中的安装指向向量为(-0.598, -0.795, 0.098)。仿真参数如表1所示，其中，约束指向和强制指向向量均为单位向量。

d=0.0001×

(32)

干扰观测器参数δi=0.01,li=100,Γ1=6.5×10-3,Γ2=2×10-7,Γ3=2.3×10-6；控制器参数k1=4,k=200。

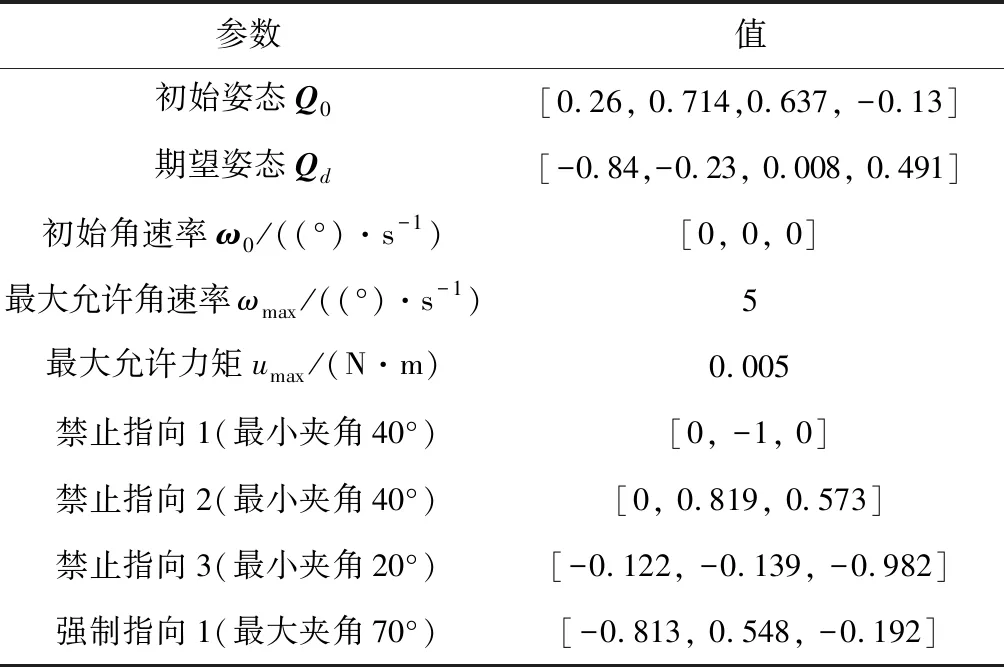
表1 仿真参数Table 1 Simulation parameters

3.1 姿态机动方法对比

本节重点研究卫星从初始姿态机动到期望姿态的过程中需要避免三个禁止指向(CO1, CO2, CO3分别对应禁止指向1, 2, 3)和一个强制指向约束的情况。为校验本文方法的有效性，本文方法与文献[7]中的方法进行对比，仿真对比中不考虑外界干扰的影响。文献[7]中的控制律如式(33)所示：

(33)

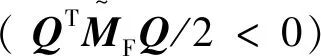
由图5可知，采用本文方法能够保证姿态角速率始终满足|ωi|≤5°/s,i=1,2,3，而文献[7]方法则超出了角速率允许范围。图6表明本文方法在满足多种类型约束的同时所需控制力矩较小，|ui|<0.005 N·m，适用于控制能力较弱的微小卫星。

3.2 干扰情况下仿真对比

本节主要检验在外界扰动力矩作用下本文算法的有效性。外界扰动力矩具体形式如式(32)所示，图7～图9为在有干扰补偿和无干扰补偿(即式(27)中的D=0)两种情况下本文姿态约束控制算法的仿真结果。

如图7、图8所示，即使干扰存在，本文方法依然能保证卫星姿态在满足约束指向的同时最终收敛到期望姿态。且可以看出，加入干扰补偿的控制律相较于未加入干扰补偿的控制律姿态指向精度更高，姿态稳定度更好。图9则表明卫星姿态角速率始终处于约束区间|ωi|≤5°/s,i=1,2,3。综上所述，本文提出的方法能够满足卫星多重姿态指向约束和角速率约束且最终能够收敛到期望姿态。与此同时，由于引入了自适应干扰估计律实现对外界扰动力矩上界的估计和补偿，进一步提高了控制系统的指向精度和鲁棒性。从而为微小卫星多约束姿态规划提供一种新的解决思路。

4 结 论

本文针对微小卫星多重姿态指向约束和角速率约束问题提出了一种基于对数型势函数和障碍Lyapunov函数相结合的姿态机动规划方法。在保证被控姿态指向约束和角速率约束的条件下，最终指向期望姿态。该方法实时性好、计算量小，且所需控制力矩小，因此非常适合于星上计算能力有限的微小卫星姿态控制。此外，本文还设计了非线性自适应干扰估计律，对外界干扰力矩的上界进行了估计并将估计值引入控制律进行干扰补偿，从而增强了控制系统的鲁棒性，提高了姿态指向精度和稳定度。仿真结果表明，该方法能确保被控姿态指向期望姿态过程中始终满足指向约束和角速率约束，且具有较好的鲁棒性。