火箭垂直回收多阶段最优轨迹规划方法

邵 楠，闫晓东

(西北工业大学航天学院，西安 710072)

0 引 言

火箭从高空返回并垂直定点着陆回收是火箭重复使用的一种重要方式。对于火箭垂直回收任务而言，回收过程不仅要进行减速并精确着陆，还要满足返回过程中各种过程约束，此外还要使得燃料消耗最小。由于火箭回收的初始高度比较高，一般而言，整个返回弹道可以分为三段：动力减速段、气动减速段和动力着陆段。动力减速段为使火箭动压降低至满足栅格舵工作条件的状态；气动减速段对射程起到调制作用，并尽可能地利用气动力降低终端位置误差；动力着陆段需要满足位置、速度、姿态等终端约束实现定点垂直着陆。

由于火箭回收制导任务的复杂性，满足多约束条件并具有快速收敛特性的制导算法一直是众多学者研究的方向。文献[1-3]提出了一种凸规划算法，用于求解火星精确着陆相关的最小燃料动力下降制导问题。他们提出“无损凸化”的概念，使得非凸控制约束的轨迹优化问题转化为一个有限维二阶锥规划问题，并在该问题的基础上进一步引入推力指向约束，使改进的动力降落制导算法对推力约束和推力指向约束都产生了无损凸化。该方法忽略了气动力的作用，通过线性搜索步骤确定终端时刻，无需迭代即可算出最优解[4-6]。然而其固定的终端时刻，无法保证开机-终端时刻组合的最优性。文献[7-8]进一步提出了一种以燃料最优为指标的动力着陆问题的逐次凸化算法并给出了逐次凸化的证明。在该算法中，引入了气动阻力和包括自由终端时间在内的各种非凸约束，通过逐次凸化、逐次线性化虽然增大了计算量，但是能够解决更复杂的约束情况[9-11]。王劲博等[10]针对火箭动力定点垂直着陆提出一种高精度快速轨迹优化算法，算法将凸化技术与伪谱离散方法有机结合，将非凸、非线性优化问题转化为凸优化问题，进而充分利用凸优化的求解快速性、收敛确定性以及伪谱法离散精度高的特点，实现了考虑阻力的两阶段轨迹优化。从优化结果看，虽然两阶段最优规划方法比单独的动力下降段最优规划可以节省更多燃料，但是当前多阶段最优轨迹优化方法仅考虑了阻力的影响。事实上，由于火箭倒飞时底阻较大，在气动减速段存在一定的配平攻角，火箭所受的升力也十分显著，特别是当攻角可由栅格舵调节时，升力也可控。这种情况下，过程约束和优化结果产生很大的不同。

基于此，本文考虑完整的气动力，将气动力、推力以及发动机点火和关机时刻均作为控制变量，基于无损凸优化方法研究了多阶段垂直返回着陆轨迹优化方法，以最大程度利用现有火箭气动减速能力，减小燃料消耗，并满足各种过程约束和终端约束。考虑到气动减速段飞行时间久、飞行距离长，且气动减速段过程中升阻力控制量变化平缓，使用Legendre-Gauss-Radau伪谱法[12-15]，对气动减速段进行离散，减少计算量同时提高运算精度。同时，动力下降段由于推力突变的非光滑性，在无损凸化的基础上采用等距离散的方法构建了凸优化问题。最后通过对多阶段离散最优控制问题进行无损凸化，将原问题转换为二阶锥规划问题，从而实现了火箭多阶段定点垂直着陆最优轨迹的快速规划。

1 模型建立

建立着陆表面固定参考系。由于着陆段飞行距离较短,假设在整个着陆过程中地表为一个平面。

建立地面参考坐标系：坐标系原点O位于着陆点。OX轴位于水平面，指向火箭初始位置方向为正，OZ轴垂直于水平面，向上为正，OY轴与其他两轴构成右手直角坐标系。

在地面参考坐标系下，火箭的三自由度动力学方程为：

(1)

(2)

(3)

其中，r(t),v(t)和m(t)分别为火箭的位置矢量、速度矢量和质量。火箭发动机推力矢量T(t)方向与火箭体轴一致，Y(t)为火箭升力，D(t)为火箭阻力，定义火箭速度矢量与纵轴之间的夹角为总攻角η，升力和阻力为：

(4)

(5)

总升力方向与速度方向垂直：

YT(t)·v(t)=0

(6)

其中，SD为参考面积，大气密度使用标准大气模型，通过特征点选取

(7)

(8)

由于再入返回过程中箭体法向过载不能太大，一般总攻角要约束在较小的范围内，因此有：

|η|≤ηmax

(9)

(10)

考虑到火箭返回段射程较小，因此重力加速度g可表示为：

(11)

g为重力加速度大小：

(12)

式中：Re为地球平均半径。

2 多阶段离散优化模型

2.1 气动减速段

伪谱离散方法布置N个离散点，可以获得最高2N+1次代数精度。相对其他离散化方法具有离散精度高及收敛速度较快的优势。气动减速段飞行时间久、飞行距离长，且气动减速段升阻力控制量连续变化，因此气动减速段更适宜采用伪谱离散方法。使用Legendre-Gauss-Radau伪谱法，为气动减速段布置N1个离散点，对气动减速段进行离散：

(13)

L为Radau微分矩阵，k=1,…,N1-1；f(x,u)为式(1)～(3)中微分方程的右端函数;τk为[-1,1)区间内的配点;x=[rT,vT,m]T为滑行段的状态变量。由于总攻角可调节，升力也可调节，可将升力作为控制变量，因此，控制为u=[TT,YT]T。

由于Radau配点不包括最后一个端点τf=1，因此还需满足如下约束：

(14)

采用伪谱方法离散后的动力学方程为：

(15)

气动减速段火箭发动机不开机，因此推力T[k]=0，火箭总升力方向满足与速度垂直约束，升力阻力满足于总攻角的约束，离散的控制量约束为：

(16)

边界条件满足初始时刻状态约束：

(17)

2.2 动力着陆段

动力着陆段推力在最大和最小推力间变化，可能出现不连续情况，使用Legendre-Gauss-Radau离散会导致计算精度下降，因此采用均匀离散方法，设离散布点数为N2，则该段终端时间为：

(18)

(19)

其中，k=N1,N1+1,…,Nf，动力学方程状态的初始和终端约束为：

(20)

其中，mdry为火箭干重，rf和vf分别为要求的终端位置和终端速度。除状态约束外，还需要对动力下降段的推力大小和推力指向进行约束：

(21)

(22)

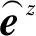
(23)

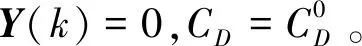
2.3 最优控制问题模型

综上，以燃料消耗最优为性能指标的火箭自主返回垂直着陆轨迹优化问题(问题1)为：

maxJ=m[Nf]

s.t. 式(13)～(17)，式(19)～式(23)

(24)

问题1为燃料消耗最优火箭自主返回垂直着陆轨迹优化问题的原始问题，由于分母的质量项、气动力非线性以及自由时间变量的引入导致问题1是非凸的。

3 问题的凸化

由于问题1的约束是非凸的，不能应用凸优化技术来求解，因此需要对原问题的约束进行凸化处理。针对推力矢量约束的非凸性，本节通过无损凸化方法进行凸化，非线性动力学方程和其它非线性约束通过逐次线性化的方法转化为线性约束，最终原问题被转化为二阶锥规划问题。

3.1 无损凸化

针对原非凸问题提出对应的松弛凸优化问题，通过增加问题的维度,将原非凸可行域适当松弛放大，构成高维的凸可行域，并通过极大值原理保证松弛问题的最优解仍在原问题的可行域内，凸化原理如图2所示。

引入松弛变量Γ(t)对原控制约束进行松弛，将原控制变量约束做如下变换：

(25)

Tmin≤Γ(t)≤Tmax

(26)

3.2 逐次凸化

在动力学方程和其它非线性约束中，非线性主要来源于气动升力/阻力、分母项中包含的质量项以及状态与发动机开机时间和发动机关机时间的乘积。这些非线性特性通过逐次线性化的方法予以线性化。

1)动力学方程约束线性化

在动力学方程约束(13)中，矩阵L是常数矩阵，非线性主要来源于包含终端时间的动力学方程：

(27)

对式(27)在第i次迭代结果处进行一阶泰勒级数展开，取其线性项得：

(28)

(29)

式(28)中，在离散点处的常数矩阵为：

将式(28)代入式(13)，得到线性化的动力学方程约束为：

(30)

对于等距离散的动力学方程(19)，采用相似的离散化方法，此处不再赘述。

由于引入升力控制量，式(16)增加了一个非线性约束：

YT[k]·v[k]=0

(31)

采用一阶泰勒级数展开线性化为：

YT[k]·v[k]=Yi[k]·vi[k]+YT[k]·

vi[k]+YiT[k]·v[k]

(32)

2)信赖域约束

由于线性化是在上次迭代结果上进行的，因此若两次迭代结果相差比较大时，可能使问题无解。为了减少这种风险，希望确保线性化所涉及的变量不会与前一个迭代中获得的值发生显著偏离，因此需要引入信赖域约束来保证线性化的可行性。

将第i+1次迭代变量与第i次迭代变量结果之间的差约束到一个范围内有：

|xi+1-xi|≤ex

(33)

|ui+1-ui|≤eu

(34)

其中，ex和eu分别表示容许的偏差值，可提前设定为固定常数，也可以根据线性化偏差不断更新。

3)松弛

在逐次迭代的初期，特别是当选取的初始弹道与最优解相差较大时，可能由于线性化造成“伪不可行”现象，即原问题存在可行解，线性化后退化为不可行问题。在这种情况下，不可行性阻碍了迭代过程，阻碍了收敛。一种解决方法是对式(30)添加松弛变量，并把松弛变量加入到性能指标中最小化，松弛约束为：

(35)

式中:Ω(τk)为松弛变量。

由于引入升力控制量，式(16)经过一阶泰勒级数展开线性化为(32)，该式过于严格，在线性化迭代求解中需要进行松弛以获得更好的迭代结果：

YT[k]·v[k]<=y(k)

(36)

(37)

式中：kΩ,k是系数向量，调节该系数向量使得松弛变量趋于0。

4 无损凸化的最优控制问题及其求解

4.1 无损凸化以后的优化问题

问题1经过无损凸化、线性化和松弛，得到由不等式约束、等式约束和二阶锥约束构成的问题2：

s.t.

(38)

原始问题1经过对推力凸化处理后，得到了新的问题2。可以证明，该凸化过程是一种无损凸化，因此问题2与问题1是等价的[1]。

文献[7]针对非线性动力学、非线性过程约束以及二阶锥约束的序列凸化算法进行了一阶条件下的收敛性证明。本文中经凸化处理后问题2是一个典型的序列二阶锥规划问题，根据凸优化理论[16]，问题2的解序列至少存在一个聚点，该聚点为原问题的驻点。因此，在一阶条件下，证明序列凸优化过程是收敛的，并且当信赖域约束动态调整时，具有超线性收敛特性。

4.2 以射程为性能指标的凸优化问题

为了比较升力对射程的影响，以射程最大和最小为性能指标，构建问题3，其边界约束与过程约束与问题2有所不同，修改如下。

修改性能指标(38)，分别以最大射程和最小射程为性能指标：

最小射程：

最大射程：

终端位置约束式(20)中，由于航向位置作为性能指标，因此去除航向位置约束：

(39)

由于终端位置不再是原点，修改下滑斜率约束式(23)，使下滑斜率约束随终端位置变化：

(40)

虽然性能指标和约束有所不同，但问题3依旧是一个典型的序列二阶锥规划问题。

4.3 问题求解过程

问题2和问题3是一个序列二阶锥规划问题，需要通过序列凸化算法进行逐次迭代求解。在迭代求解时，首先需要提供一组状态初始剖面，一组良好的初始剖面有助于迭代过程快速收敛到最优解。

基于该初值，针对问题2进行迭代求解，直到两次优化结果状态量的差满足收敛条件为止。图3为迭代求解流程图。

5 仿真校验

仿真算例分别计算了无升力轨迹优化和升力可控轨迹优化，对比说明了加入升力后对最优燃料性能指标的影响。选择某型火箭作为仿真模型，任务初值与终端约束如表1所示。火箭飞行参数与气动参数如表2所示。

参数值v0/(m·s-1)[-500 -10 -70]Tvf/(m·s-1)[0 0 0]Tr0/km[41.5 0.2 47.2]Trf/km[0 0 0]T

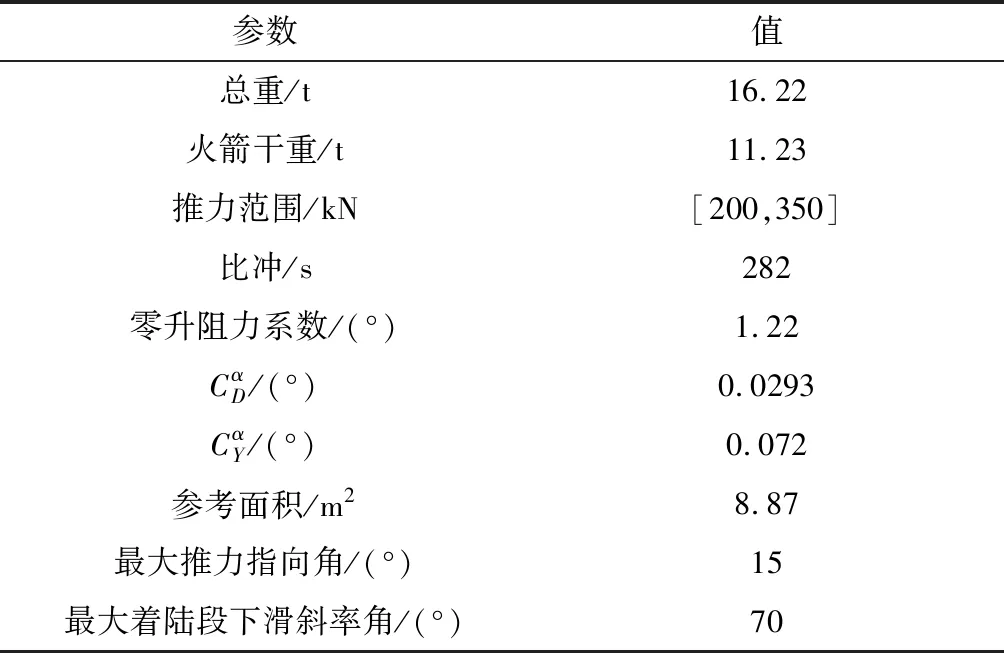
表2 火箭参数Table 2 Parameters of rocket

本文所有数值计算在MATLAB 2017b环境下编制及运行，采用CVX优化工具箱和MOSEK 8.0.0.60作为算例的凸优化求解工具。

5.1 无升力算例

该算例不考虑升力作用，在气动减速段仅有气动阻力作用。气动减速段和动力着陆段各为30个离散点。火箭飞行时间作为优化变量，优化后火箭总飞行时间为135.7 s，其中气动减速飞行时间为123.7 s，动力着陆段飞行时间为12.0 s。关机后火箭质量剩余14.89 t，总燃料消耗为1.33 t。

图4为逐次凸化迭代后气动减速段的三维轨迹，表明火箭成功在预定落点降落，图中所示圆锥为下滑斜率约束面。从图5、图6可以看出，位置和速度均收敛到预定终端状态。经过空气阻力减速，发动机开机点的坐标为[114.7， -140.8， 1089] m，初始速度为[-19.38， -0.33， -180.3] m/s。

图7为火箭发动机推力大小和三向推力曲线。从仿真结果可以看出，气动减速段推力为0，气动减速段后，火箭先以最小推力工作，然后切换到最大推力状态。

5.2 气动升力作为控制量仿真算例

本算例考虑气动升力，且气动升力大小能够由总攻角进行调节，总攻角约束为：|η|≤15°。优化后火箭总飞行时间为144.0 s，其中气动减速段飞行时间为135.1 s，动力着陆段飞行时间为8.9 s。关机时刻火箭剩余质量为15.09 t，燃料消耗为1.13 t。相比无升力轨迹优化燃料节省0.2 t。

图8、图9表明速度和位置满足终端约束。动力着陆段初始的坐标为[222.1, -105.3, 534.8] m，初始速度为[-54.03, 25.65， -125.9] m/s。

从仿真结果可以看出，有升力情况下发动机的开机高度明显降低，速度矢量的方向更趋近于减少位置误差的方向，从而导致发动机工作时间缩短，更加节省燃料。

图10为火箭总攻角η随时间变化曲线，最大攻角为15°，可以看出攻角满足约束条件。

5.3 升力对射程调制对比

通过求解问题3，可以获得回收过程的最小射程和最大射程。对于无升力情况，最小射程为41.232 km，最大射程为41.867 km，落点射程调节范围为0.623 km。由于无法对升力进行调节，射程调制主要由推力调节来实现，因此图11仅给出动力下降段的纵向轨迹曲线。不难发现，由于存在最大燃料、推力指向、推力大小以及下降斜率约束，射程调节范围较小。

图12为以升力可控情况的最小、最大射程轨迹。火箭飞行最小射程为36.97 km，最大射程为47.171 km，落点射程调节范围为10.201 km。相较于无升力控制算例，可大幅提升可达域范围。

6 结 论

本文针对火箭垂直回收提出一种将气动减速段与动力着陆段统一规划的多阶段燃料最优轨迹规划算法。该算法通过将原问题进行无损凸化，并经过线性化和离散化，得到序列SOCP问题，可快速迭代求解。通过仿真校验，可得出如下结论：

1)将气动力作为控制变量时，仍可对原问题进行无损凸化。

2)将发动机开、关机时间作为优化变量有助于获得全局燃料最优解。

3)在气动减速段调节升力，可以获得更大的射程调节范围，并可以进一步节省动力着陆段的燃料。