西北地区双子座超高层建筑的水准测量路线平差计算方法及精度评定

刘雪涛

摘    要：西北地区双子座超高层建筑对水准测量路线的精度要求高，按照三等水准测量对首级高程控制点进行测量，按照加权正比例反向分配的方式，利用简易平差方法对水准测量路线进行平差计算，求得未知控制点的最或是值，并对其精度进行评定。

关键词：超高层;水准路线;平差;精度评定

1  前言

一般群体超高层建筑占地面积大，布设的水准路线较长，而各个建筑利用的控制点又不完全相同，为保证所有建筑物的控制点精度等级相同，就要把各建筑物的首级控制点布设在同一个水准路线中。而对称建筑，在施工过程中必须保证各个建筑物向上传递后的高程误差范围相同，这就势必要提高建筑物首级水准控制路线的精度。在普通工程测量中，一般测量员对经典平差方法等高精度的计算方法不熟悉，难以进行即时数据处理，本文以银川市绿地中心项目为依托，运用加权正比例反向分配的简易平差方法进行平差计算，并对平差后的水准控制点精度进行评定，为同类型的工程测量提供参考。工程位于银川市中阿之轴，其中的两栋建筑地下4层，地上66层，建筑高度301m，为中国西北第一高楼，是西北地区地标性建筑。

2  水准测量路线布设

本场区内没有已知点，需要从场外引测，场外已知点高程系统采用1956年黄海高程系统。从整体考虑，按照先整体后局部，高精度控制低精度的原则。为保证每个建筑的首级高程控制点精度等级相同，需要把各建筑的首级控制点布设在同一个水准控制路线内。现以本工程的双子座超高层为例布设水准控制路线，已知水准点A、B，分布在场区外的东侧和西南侧，根据施工现场平面布置情况，考虑通视条件和易于保护等条件，在场区内布设待测水准点S3、S5、S7、S9，水准点用混凝土筑成，四周用钢管保护，与已知点形成附合水准路线，以已知点A为起始点，途径S3-S7-S9-S5，引测至已知点B。

图1  控制点和水准路线示意图

3  水准测量技术参数

三等水准测量采用DS3水准仪测量，转点采用尺垫支撑水准尺，视距≤75m，前后视距差≤2.0m，每站的前后视距积累差≤5.0m。每测站读取基本刻度和辅助刻度数值时采用“后视-前视-前视-后视”的原则，每千米高差全中误差≤6mm，水准路线长度≤50km，按照往返各测量一次的方法，测段、路线往返测高差不符值≤±12[K]mm，闭合差≤±12[L]mm。其中，K为测段或路线长度（km）;L为附合路线长度（km）。

4  平差计算

4.1  实测数据整理

已知点A、B的高程为HA=1109.091m，HB=1107.506m，两点间的实测高差以h表示，如已知点A与待测点S3的高差为hA3，S3与S7点的高差为h37，引测至已知点B时，B点的实测数值以B测表示，测量实际数据如表1中所示。

4.2 平差计算

通过表1中的实测数据可以看出，由于存在测量的误差，B点的实测值与已知值不等。

首先计算附合水准路线的闭合差f实，即：f实=HA+∑hi-HB=6mm。

按照反向分配的原则，高差改正数v=-f实，即vi=-6mm。

各测段间的距离区别较大，所以高差改正数的分配以测段距离进行定权，测段i的权值为Pi，测段i的距离为Li，即：Pi=1/Li，计算得各测段的权值分别为PA3=9.76，P37=6.28，P79=10.41，P95=7.99，P5B=16.91，总权值P=51.35。

按照最小二乘法，测段i的高差改正数vi与测段的权值Pi成反比，即与测段的距离Li成正比，即vi=-f实×Li/∑L，计算可得vA3=-1.13mm，v37=-1.76mm，v79=-1.06mm，v95=-1.39mm，v5B=-0.65mm。

根据计算出的高差改正数，可以计算出平差后的高差hi=hi+vi，进而计算出各个待测点的高程Hi，即：

H3=HA+hA3+vA3=1107.954m，H7=H3+h37+v37=1107.581m，H9=H7+h79+v79=1107.375m，H5=H9+h95+v95=1107.555m，HB平差=H5+h5B+v5B=1107.506m。

即，平差后，HB平差=HB。

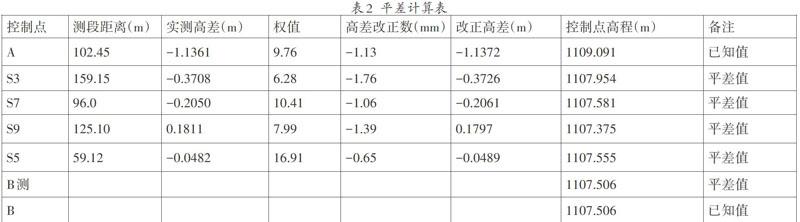
平差计算表及成果如表2所示。

5  精度评定

测量后，水准路线的闭合差f实为：f实=HA+∑hi-HB，代入数据后f实=6mm。

二等水准测量的允许闭合差：f允许=±12[L]，代入数据后f允许=8.8336mm，即，f实≤f允许，说明实际水准测量数据正确，精度满足规范要求，可以对平差后控制点进行精度评定。

根据误差积累的理论可知，在水準测量路线中，距离起算水准点最远的水准点，其误差是最大的，通过计算可知水准点S5距离已知点最远，故精度最低，应对S5的精度进行评定。

首先计算单位权中误差μ：μ=±[Pvvn-1]，式中，n为水准路线测段数，t为待测水准点的个数。代入数据后，μ=±4.07mm，

水准点S7的高程中误差为m7：m7=±[μP]，即m7=±0.57mm。

《城市测量规范》规定，三等水准测量最弱点高程中误差相对于起算点不得大于20mm，显然最弱点的精度满足规范要求。

6  结论

通过理论分析与实际测量计算，证明在西北地区双子座建筑中，按照正比例反向分配的方式，运用简易平差方法对水准控制路线进行平差计算，把抽象的平差理论转变成便于计算的方法，其精度满足规范要求。在西北地区、超高层和对水准测量等级要求较高的同类工程中，均可参考这种平差方法。本次精度评定通过理论分析和实际数据计算，验证了结论，对西北地区双子座和群体超高层建 筑的水准测量路线的计算和精度评定提供了参考价值。

参考文献：

[1] 武汉大学测绘学院测量平差学科组编著.误差理论与测量平差基础[D].武汉大学出版社，2014

[2] 张琦，修涛.单一结点或附合的水准路线的精度评定[J].露天采矿技术，2013（2）.

[3] 黄荣全.不同平差计算方法对导线测量精度的影响[J].铁道建筑技术，1996（3）.