基于傅立叶变换的音乐可视化创作方法研究

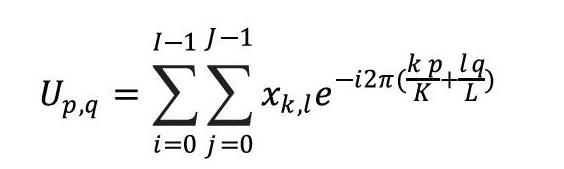
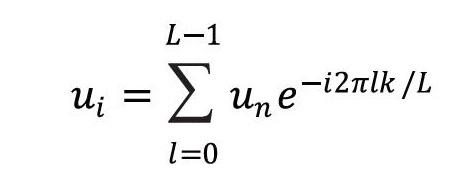
摘 要 本文研究了基于傅里叶变换的音乐与视觉的互动形式，提供了一种可视化的方法，这种可视化方法可用于音乐学相关的研究，以及互动媒体创造方法中。

关键词 音乐;可视化;FFT;傅立叶变换

在音乐创作领域中，近些年出现了探索音乐与视觉之间的关系的研究方向。有很多方法可以将音乐“转换”为二维（或三维）视觉效果（图像，视频），尽管它们始于手动转换，现在有许多自动转换的方法进行逆向转换（从视觉到音乐）的方法较少，主要涉及声音化而不是输出音乐。而且，许多流行的可视化工具都使用声音而不是音乐作为输入（例如，媒体播放器），因此，除了音乐本身之外，这种可视化还受到乐器音色和人类演奏的影响。仅将抽象音乐符号作为其输入的可视化将提供对音乐结构而不是特定音乐录音的一般特征的洞察。

傅立叶变换是检测信号周期性的工具。它在分析音频和声音时非常有用，因为它可以在短时间内（通常为100ms）提供声音的频谱。如果在水平时间线上垂直绘制一组这些频谱（低频在底部，高频在顶部），则将获得二维频谱图。这样的频谱图显示了随时间变化的频率（音符）和谐波，等效于计算机音乐音序器软件中使用的钢琴侧倾图，但未显示或编码较高级别的内部音乐结构和较长的周期性。

傅立叶变换（FT）通常显示信号的周期性，但是也可以用于将一般的非周期性信号变换为其傅立叶分量。基于这样的想法，可以尝试将FT方法应用于音乐结构本身。在这种情况下，与典型频谱计算的FT相比，必须覆盖更长的时间。这样较长的时间窗（一维）FT的输入信号可能是音频信号本身。这样的FT频谱将显示高频分量的经典FT频谱（等效于音乐音符本身），但也有望显示出此类音符变化的低频结构（<10Hz）。由于需要较长的时间窗（>0.5秒）来计算FT，因此对此的计算要求相对较高。一种更简单的方法是将一段时间内的音乐事件单独视为此“慢速”FT的输入，而不是计算整个频谱。这导致了使用二维钢琴滚动图作为输入的想法：它们基本上是二维声谱图，显示了音符在设定的时间窗口内随时间的分布。如果将二维FT算法应用于该图，则所得二维FT将显示与音符随时间和音高分布相关的特征。实际上，这是应用于一维FT（频谱）的时间图的二维FT。

这种FT计算方法已经在20世纪60年代开发出来，该技术已用于诸如语音识别之类的信号处理应用中，但尚未应用于音乐。本文中研究的是如何将FT用于可视化音乐。

1算法分析

下列等式中给出了使用复数表示法的一维离散FT的基本方程。是离散采样波输入，这些方程式以复数形式表示。

对于二维离散FT，必须在输入数组的两个轴上进行求和。二维FT通常用于图像处理，图像分析，压缩和过滤。在下面的中给出了用于计算具有点的阵列上的结果FT的等式。

尽管FT的输入可以只是虚部为零的实数数组，但生成的FT通常是复数的数组，每个复数也可以显示为具有幅度和相位的数组。对于可视化，通常大小是有意义的变量，但是为了保持输入要素的正确时间线关系，相位也是必不可少的。

一种快速计算FT的算法是20世纪60年代开发的快速傅立叶变换（FFT）算法，它可将复杂度降低到将二维FT计算为复杂度。该算法在计算频谱的许多应用中使用[1]。

2数字音乐信息提取

从音频信号中提取信息的方法称为基于内容的音频处理。它是音乐信息检索（MIR）的众多学科之一，MIR可以从音频信号计算许多特征。由于这些特征描述了音频数据的各个方面，因此它们被称为描述符。在音频处理的上下文中，有三种类型的描述符：低级描述符是直接或在变换后根据信号计算的。中级描述符描述了音乐流派或音调等特征。用于计算这种信息的算法将音频信号的特征与参考数据进行比较以用于分类目的。高级描述符描述了包含语义的特征，如“快乐”或“悲伤"。由于对高级特征的感知是主观的，因此算法要基于其他歌曲的用户评级来计算这些特征。

基于内容的音频处理源是PCM音频信号，其首先被分成帧。这些帧表示在信号的几毫秒范围内的时间间隔，是进一步计算的基础。典型的帧长约为20ms。在执行计算之前，将处理函数应用于每个帧，以便将开始和结束处的不连续性最小化。此外，連续帧通常有一些重叠，要允许效果更平滑的分析。最后，对于每个帧，计算每个描述符的一个标量值。

Processing处理核心API不支持音频，但开发社区提供了此功能的库。其中一个是Minim，包括声音访问，处理和分析等功能。Minim支持播放WAV，AIFF，AU，SND以及MP3文件，并提供从处理中访问音频信号的方法。它还允许通过音频缓冲区直接访问播放歌曲的信号，音频缓冲区可从左，右和混合区访问。这些缓冲区提供对要播放的下一个样本的缓冲和同步访问。因此缓冲器中写入的音频帧是特征提取和可视化的基础。虽然Minim还可以分别访问保存左右扬声器信号的缓冲区，但本文讨论的可视化仅使用混合缓冲区，其中包含两个通道的混合。当通过Minim.loadFile加载音频文件时，可以指定缓冲区中包含的样本数[2]。

3可视化方法

音乐可视化的一种简单方法是以原始形式可视化帧数据-即缓冲数据。这可以通过从draw方法内部访问混合缓冲区来轻松完成。然后可以通过将缓冲区长度映射到窗口的宽度和样本值来可视化缓冲区数据，音频信号的一小部分图形，也称为波形。

Minim提供了一个可用于实现转换的STFT。FFT类提供了许多有用的方法，可用于计算强度平均值或将频带映射到频率等。它还可以配置为在转换之前自动将汉宁窗口应用于缓冲区数据，从而使得结果平滑。最简单的形式是，所获得的数据可以通过将频带的数据映射到窗口宽度以及将频带的强度映射到窗口的高度来可视化，这类似于用于波形可视化的方法。

另一个有用的可视化是频谱图，它显示了信号的频率分布如何随时间变化。谱图可以揭示可用于识别目的的模式。最简单的形式是谱图具有三个维度：水平轴表示时间，垂直轴频率，颜色表示给定频带的强度。这意味着特定时间的频率由可视化中每个点的颜色表示。

在Processing中实现谱图可视化并不像到目前为止所描述的可视化那样简单。基本上，通过将表示时间的计数器映射到显示窗口的水平位置，将频带映射到窗口的高度以及将频带的强度映射到颜色来计算频谱图。问题是需要在以前的绘制调用中计算的数据。一种方法是使用诸如LinkedList之类的集合，该集合可以保存在当前和之前的调用绘制期间计算的频率数据。然后可以从集合中读取最后的w值（w是显示窗口的宽度）并使用该数据进行绘制。可以从集合中删除较旧的值。这种方法的问题在于效率非常低，因为每次调用绘图时都必须访问和绘制wn（n表示频带的数量）值。

解决此类问题的方法是基于所谓的屏幕外缓冲区的使用。在最简单的情况下，这样的缓冲区只是像素值改变的图像（PImage类的对象）。此外，Processing提供了PGraphics类，一个离屏渲染缓冲区，支持与Processing相同的绘图功能，可以像普通图像一样显示。通过使用缓冲器，以有效的方式实现光谱图可视化。首先，初始化具有宽度w和高度n的缓冲器，以及设置计数器c为零。然后，在每次调用绘制时，c递增，并且基于当前音频帧的频率信息用于绘制离屏缓冲器的c行。然后，缓冲区显示Processing的图像，直到c>w。但此方法最终会超出缓冲区宽度，解决方案是在发生这种情况时将c重置为零，即开始新的迭代。使用此方法，当前迭代的值将覆盖上一次迭代的值。

本文介绍了一种音乐可视化的方法，它是Processing的众多应用领域之一。讨论了如何访问音乐，通过计算机从音频数据流中获取信息。介绍了使用Processing音乐可视化支持庫，这个库基于FT，可以用于音乐频谱的视觉表现。它提供了一种可逆的方式来检测音乐的特征和结构，从而提供了可视化和音乐创作的新方式。

参考文献

[1] 列阿斯.Processing语言权威指南[M].北京：电子工业出版社，2013：51.

[2] Rao K R，Kim D N，Hwang J J.快速傅里叶变换：算法与应用[M].北京：机械工业出版社，2013：77-78.

作者简介

陈珏（1972-），男，江苏省苏州人;毕业院校：东南大学，学历：本科，中级讲师/工程师，现就职单位：苏州工艺美术职业技术学院，研究方向：交互设计。