轨道交通异步牵引电机无速度传感器 矢量控制技术分析
杨北辉 钟立群 朱龙胜


摘 要:介绍适用于轨道交通的异步牵引电机无速度传感器矢量控制方法。分别从控制原理、不同调制模式的切换、基波电流提取、带速重投以及黏着控制方面对轨道交通中列车异步牵引电机的矢量控制原理进行说明。着重阐述如何根据异步牵引电机数学模型采用全阶磁链观测器观测出异步牵引电机的转子磁链,利用转速估计计算,实现异步牵引电机无速度传感器的转速估计。仿真和实验结果表明,该方法可以实现转速的快速和准确估计,系统具有良好的动静态性能。
关键词:轨道交通;异步牵引电机;无速度传感器;速度估算;带速重投
中图分类号:U264
0 引言
随着中国经济的快速发展,城市人口大量增加,城市通勤运输量扩大,地铁、轻轨等大运量交通工具日益成为解决城市拥堵和绿色发展的重要手段[1]。通过多年引进消化吸收及再创新,轨道交通电气牵引系统作为车辆系统核心子系统已经基本实现自主化[2-5]。但是作为电气牵引系统核心技术之一的无速度传感器矢量控制技术却未大规模推广,速度传感器一般安装在牵引电机端部,工作环境差、电磁干扰和振动冲击大、温升高,使得速度传感器可靠性较低,维护困难。而无速度传感器矢量控制技术可以显著提高系统可靠性,减小牵引电机体积、节省安装空间、节约成本及减少维护等优势,是目前国内牵引新技术开发领域的热点[6-8]。
1 矢量控制原理
1.1 原理说明
矢量控制的原理是基于交流电机的电流控制,把交流电流按磁场坐标轴分解为转矩分量和磁场分量,分别进行控制。因此,矢量控制为了获得良好的快速响应性能,需要及时高精度的检测电机转速。
为了解决速度传感器带来的问题,采用异步牵引电机无速度傳感器矢量控制方案,通过构造虚拟的速度传感器数学模型,利用软件算法模拟电机特性,实时估计电机转速和转子磁场位置。该方案不需要对牵引系统的硬件设计进行更改,只需在原有电机矢量控制算法上增加转速估计模块。
异步牵引电机无速度传感器矢量控制原理如图1所示。由图1可知,通过电流传感器采集逆变器侧三相交流电流is,对其进行坐标变换分别得到电机静止坐标系下的电流isα、isβ和电机旋转坐标系下的电流isd、isq;基于异步电机的数学全阶模型,构造全阶磁链观测器,观测出异步电机的转子磁链 和电机静止坐标系下的电流,利用转速估计计算得到估计的电机转子角频率 ,利用异步电机数学公式进一步计算得到估计的旋转坐标变换角及电机转矩 。通过对司机手柄给定力矩T*及列车速度vt进行再黏着优化控制后,计算得到转矩电流分量,通过查表得到与电机估计转速对应的励磁电流指令值。电流指令值、 分别与电流反馈值isd、isq通过电流控制器得到d、q轴电压指令、,进而计算得到电压指令,最后通过脉冲宽度调制(PWM)得到两电平逆变器的驱动脉冲。
1.2 调制模式
对于地铁牵引工况,线网电压波动较大,如何充分利用直流电压,以期获得最大输出转矩,特别是牵引电机运行在高速弱磁阶段时,为了获得足够的电压,必须进行过调制。在低速采用异步调制,载波比较高时采用空间矢量调制(SVPWM),能明显减少逆变器输出电流的谐波成分。中速段采用同步调制,保持载波信号与调制信号频率比不变,1个周期内电压输出的脉冲个数和相位是固定的,最后过渡到方波。逆变器调制模式如图2所示。
调制度定义公式为:
(1)
式(1)中,Udc代表逆变器母线电压, 代表相电压峰值。
传统的分段同步调制方案采用三相分别切换的方法,保证不同调制策略之间的平滑切换。该方案存在切换时间长以及可能引起脉冲紊乱等问题,不适合在无速度传感器方案中应用。本文通过严格地理论分析,设计了基于输出电压角度补偿的快速切换方案,保证在无速度传感器控制时不同调制方案之间切换的快速性和平顺性。另外,设计了简单的PWM周期补偿方法,保证在采用同步PWM调制时输出脉冲在动静态过程中的对称性。
1.3 基波电流提取
在低开关频率的大功率变流器设计中,中高速段开关频率低于300 Hz,此时电流波形畸变严重,无法直接用于矢量控制。利用观测的基波电流作为反馈信号可以显著提高闭环控制系统在低开关频率以及过调制区域运行的稳定性和动态响应速度。
利用异步牵引电机数学模型,选取基波电流和转子磁链作为状态变量,构造观测器:
(2)
式(2)中, τσ为定子模型时间常数,τr为转子模型时间常数, kr为互感Lm和转子电感之间的比值, Rσ为定子模型等效电阻, 为基波电流的估计值, ωr为电机转子角频率,Gs、Gr分别为定子、转子模型反馈增益矩阵。基波电流观测器框图如图3所示。
合理设置反馈增益矩阵Gs、Gr,可以使观测基波电流在全速域收敛。
1.4 带速重投
当列车惰行、牵引系统出现故障或者过无电区时,牵引变流器需要封锁控制脉冲。在上述情况下,驱动系统需在未知速度情况下重新启动。为了满足电气牵引和制动安全的需求,要求列车能够实现快速重投。通过观测器反馈矩阵,可以确保估计速度在任何情况下均能收敛至实际速度。该方案具有收敛速度快,精度高等特点。
1.5 黏着控制
黏着控制系统是高阶、非线性、多耦合的复杂系统,作为列车牵引控制系统的一部分,对列车安全运行至关重要。为了保证乘坐的舒适性以及提高车轮和轨道的使用寿命,如何提高黏着控制的快速响应和实现黏着利用率的最大化显得格外重要。采用基于黏着斜率法的再黏着优化控制可通过对黏着蠕滑特性曲线斜率的判别实现道路黏着峰值点的自动搜寻,即通过对黏着系数的估计和黏着斜率的判别,实时观测列车运行状态,以达到最佳的黏着控制,有效地抑制车轮的空转/滑行现象。
根据列车动力学模型及牵引电机方程可知,负载力矩与黏着系数间的关系为:
(3)
式(3)中, TL为负载力矩,μa(vs)为道路黏着系数, vs为蠕滑速度, W为等效轴重, r为车轮半径, g为重力加速度, Rg为齿轮传动比, ηe为齿轮箱传递效率。负载力矩和黏着系数均无法直接测到,需要通过观测器的方法估算负载力矩,继而估算出黏着系数,基于扰动观测器的黏着系数观测器如图4所示。
图4中, 为负载力矩估计值, 为计算的黏着系数估计值,s为微分算子,a为截止频率,ωm为电机角速度, ωw为车轮角速度,Jw为车轮转动惯量,Jm为电机转动惯量,Tm为电机转矩,T为车轮驱动轉矩。根据图4可估计出负载转矩进而估算出黏着系数:
(4)
(5)
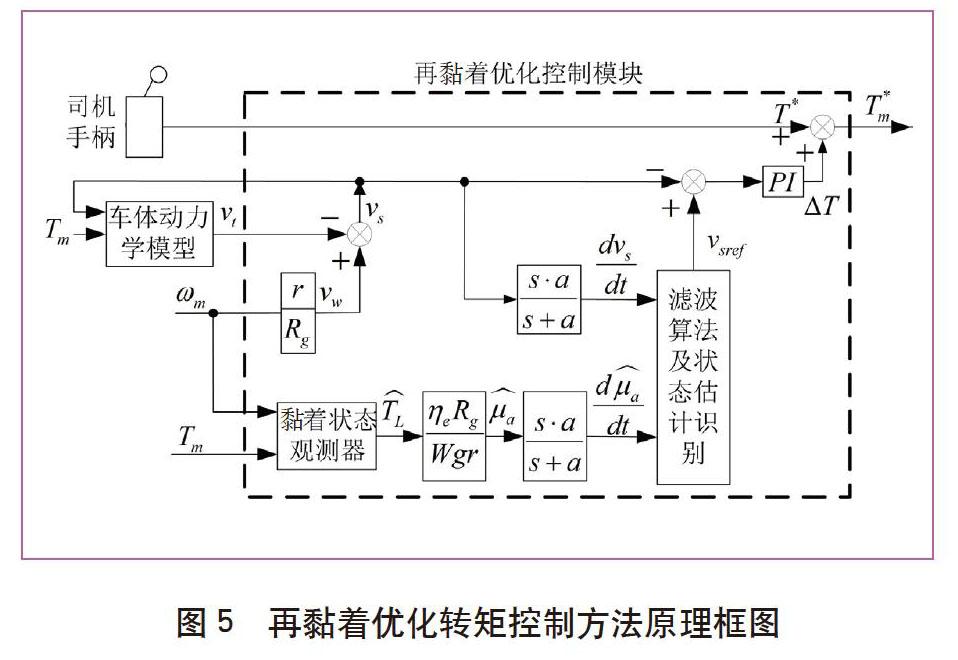
采用滤波算法和状态估计理论实现对黏着特性曲线斜率的在线识别,再黏着优化转矩控制方法原理如图5所示。
根据上述分析可知,要想实现黏着控制的快速响应,需要及时和准确的获取电机转矩和电机角速度。当采用速度传感器检测电机转速时存在约200 ms的延迟,而采用无速度传感器方式时检测延迟可缩短至20~25 ms。因此,采用无速度传感器矢量控制可满足提高列车黏着控制的快速响应性。
2 速度估算
全阶磁链观测器实际上是1个估计器,它采用了异步电机的全阶模型,并使用了1个含被观测对象变量的反馈环。采用全阶观测器观测出异步牵引电机的转子磁链,然后利用转速估计律计算得到转速。
异步牵引电机定子电压方程:
(6)
异步牵引电机转子电压方程:
(7)
异步牵引电机转子磁链方程:
(8)
异步牵引电机定子磁链方程:
(9)
式(6)~式(9)中, isα、isβ,irα、irβ为静止坐标系下的定子电流和转子电流;Rs、Rr分别为定子、转子绕组电阻; Ls、Lr分别为定子、转子自感;Lm为互感。
将静止两相坐标系下的异步牵引电机数学模型写成状态空间方程:
(10)
式(10)中,状态变量X = [isα isβ ψrα ψrβ ] T,输入变量U = [usα usβ] T ,输出变量Y = [isα isβ ] T ,系数矩阵A、B、C为:
(11)
(12)
(13)
矩阵 A、B里的系数为:
构造状态观测器:
(14)
反馈增益矩阵 :
(15)
转速估计为:
(16)
在转速自适应算法中采用比例积分方案:
(17)
式(17)中 ,为估算的电机转子角频率, KP 和 KI 为任意正增益值。
采用高精度观测器离散化方案,即使在低采样率下也可以保证观测器在全速度范围内具有良好的稳定性和较高的观测精度。另外,基于该观测器方案实现了无延迟高性能基波电流估计。
3 仿真及试验
3.1 系统仿真
为验证无速度传感器矢量控制理论分析的正确性,利用MATLAB软件搭建了牵引逆变器驱动电机进行无速度传感器矢量控制的系统仿真模型。在RTLAB平台上进行硬件在环测试(Hardware In Loop, HIL),通过基于模型的设计方法,直接进行软件集成、下载到牵引传动控制单元(DCU),用于实时仿真机模拟牵引传动系统,进行仿真实验,理论进一步得到了验证,缩短了开发周期。系统仿真参数如表1所示。
异步牵引电机从静止启动运行到高速封锁脉冲再制动,用于模拟牵引电机无速度传感器矢量控制以及高速带速重投工况,系统仿真波形如图6所示。
由图6可知,异步牵引电机无速度矢量控制在t = 0.3 s才开始启动,在t = 20~20.5 s系统封锁脉冲。电机牵引网压DC 1 500 V,制动网压DC 1 650 V。
由图6a可知,电机转矩从t = 0.3 s开始上升历时0.55 s从0 N · m达到给定力矩1 500 N · m,尽管在t = 5 s负载转矩从0 N · m突变为1 000 N · m,在t = 10 s负载转矩从1 000 N · m突变为0 N · m,电机实际转矩仍实时跟踪电机给定转矩指令,在t = 12.8 s电机进入弱磁控制,电机实际转矩逐渐减小;电机转矩指令在20.5 s从0 N · m突变为-1 400 N · m,同时电机负载转矩从0 Nm突变为1 000 N · m,电机开始制动,电机实际转矩从0 N · m历时1.9 s达到转矩指令-1 400 N · m;电机负载转矩在t = 25 s从1 000 N · m突变为0 N · m,电机实际转矩仍实时跟踪电机给定转矩指令。
由图6b可知,电机从t = 0.3 s开始加速,电机转子观测频率在程序里设定的初值为60 Hz,历时0.3 s电机观测频率能够很好地观测出电机实际频率,观测误差为0.15 Hz。在t = 20 s系统封锁控制脉冲,由于惯性电机实际转子频率保持在103.65 Hz,电机转子观测频率在封锁脉冲后突变为程序给定的初始值60 Hz,在t = 20.5 s系统进入制动,电机转子观测频率从60 Hz历时0.25 s跟踪上电机实际转子频率,稳定后跟踪误差为0.16 Hz。
由图6c和图6d可知,电机在t = 0.3 s开始启动后, 电机观测电流用了0.9 s准确观测出电机实际电流,稳定后峰值出观测误差为2 A;电机观测转子磁链用了0.6 s跟踪上电机实际转子磁链,稳定后峰值处观测误差为0.01 Wb。在t = 20~20.5 s系统封锁脉冲,此时电机实际电流和观测电流均变为0 A,电机实际转子磁链和转子观测磁链也均变为0 Wb。t = 20.5 s电机开始制动后,电机观测电流从0 A历时0.25 s跟踪上电机实际电流,稳定后电流峰值处最大跟踪误差约为3 A;电机转子磁链观测值从0 Wb历时0.2 s跟踪上电机实际转子磁链,稳定后转子磁链峰值最大跟踪误差约为0.01 Wb。
由图6e和图6f可知,电机从零速加速启动时,采用的是异步调制,随着电机转子频率上升分别切换到15分频、11分频、7分频、3分频和弱磁方波调制。在t = 20 s封锁脉冲后,电机线电压变为0 V,调制模式恢复到异步调制,由于从高速开始制动,电机从异步调制迅速逐级切换至弱磁方波调制,当电机转子频率降低后逐渐由弱磁方波逐级切换至异步调制,整个切换过程平滑无误动作。
由图6g可知,负载突变对电机三相电流无影响,但调制模式的切换会引起电机三相电流的变化。当t = 20 s封锁脉冲后,牵引电机三相电流变为0 A,t = 20.5 s电机开始制动后,牵引电机三相电流由0 A逐渐增大,三相电流平衡。
仿真结果表明,本文提出的异步牵引电机无速度传感器矢量控制的转子频率能实现迅速跟踪且精度高,PWM调制方式切换平滑无冲击,电机电流和转子磁链的观测速度快、精度高,电机三相电流平衡,整个系统具有良好的动静态性能。
3.2 系统试验
为了进一步验证本文提出的异步牵引电机无速度传感器矢量控制策略的正确性,在牵引组合试验台上进行了电机拖动试验。牵引逆变器拖动4台电机模拟A型车满载(AW2)工况,从静止启动运行至弱磁方波和带速重投实验,结果分别如图7和图8所示。
由实验结果图7可知,电机三相定子电流正弦;转矩控制效果好;在调制方式切换时,电机三相定子电流和电机转矩响应快、跟踪好。由图8可知,在系统惰行转运行工况时,电机转子频率能够实现快速跟踪,电流切换平顺,很好地实现带速重投。系统仿真和实验结果均验证了本文提出的异步电机无速度传感器矢量控制策略的正确性和有效性。
4 展望
异步牵引电机无速度传感器矢量控制技术,作为电气牵引系统的核心技术具有广阔的应用前景。在该技术开发过程中应用了基于模型设计方法以及基于RTLAB的半实物仿真,加快了研发进度,降低了研发成本。通过地面试验,该系统能够很好地满足地铁A型车牵引制动特性要求,并解决了牵引系统带速重投问题,具有推广价值。
参考文献
[1] 苑国锋,李正熙,张永昌,等. 西安地铁二号线无速度传感器牵引系统关键技术[J]. 科技纵览,2018(2):60-61.
[2] 李鑫. 轨道交通用感应电机无速度传感器矢量控制的研究[D]. 湖南长沙:湖南大学,2018.
[3] 苏杭,陈东华,孙仲兵,等. 一种无扇区判断SVPWM算法及其仿真研究[J]. 华电科技,2008,30(10):27-30.
[4] 马志文,殷振环,蒋威,等. 大功率二电平逆变器多模式SVPWM算法研究[J]. 机车电传动,2010(4):17-24.
[5] G. Narayanan,V.T.Ranganathan. Two Novel Synchronized Bus-Clamping PWM Strategies Based on Space Vector Approach for High Power Drivers[J]. IEEE Trans. Power Electron,2002,17(1):84-93.
[6] 张永昌,赵争鸣,张颖超,等. 三电平变频调速系统SVPWM和SHEPWM混合调制方法的研究[J]. 中国电机工程学报,2007,27(16):72-77.
[7] 李华,方晓春,林飞,等. 异步牵引电机方波单电流闭环控制策略及其参数鲁棒性分析[J]. 电工技术学报,2018,33(9):2034-2043.
[8] K.Ohishi,K. Nakano,LMiyashita,et al. Anti-Slip Control of Electric Motor Coach Based on Disturbance Observer[J]. IEEE/AMC98-COIMBRA,1998.
[9] 吴能峰,钟立群,杨北辉,等. 列车传动最优黏着控制策略研究[J]. 铁道机车车辆,2018,38(1):26-42.
[10] 李江紅,胡云卿,彭辉水,等.轨道交通粘着利用控制的关键技术与方法[J].机车电传动,2014(6):1-5.
[11] Jehudi Maes,Jan A.Melkebeek. Speed-Sensorless Direct Torque Control of Induction Motors Using an Adaptive Flux Observer [J]. IEEE Trans. Ind. Applicat,2000,36(3):778-785.
[12] 张永昌,赵争鸣. 基于自适应观测器的异步电机无速度传感器模糊矢量控制[J]. 电工技术学报,2010,25(3):40-47.
[13] 张永昌,赵争鸣,张颖超,等. 基于全阶观测器的三电平逆变器异步电机无速度传感器矢量控制系统[J]. 电工技术学报,2008,23(11):34-40.
[14] 王坚,年晓红,桂卫华,等.新型异步电机无速度传感器控制方法[J].中国电机工程学报,2008(3):96-101.
[15] 张永昌,杨海涛. 异步电机无速度传感器模型预测控制[J]. 中国电机工程学报,2014,34(15):2422-2429.
收稿日期 2019-08-16
责任编辑 宗仁莉

