汽车柔性管线运动仿真分析技术及其应用
卫聪敏 张三磊 王光耀 翁洋

摘要:针对汽车柔性管线的设计和布置缺乏动态仿真支持的问题,基于Cosserat弹性杆理论提出一种柔性管线运动仿真分析技术。以某车型制动软管为例进行建模和动态仿真分析,并对其动态仿真模型进行试验验证。仿真结果与实车测试结果一致性较高,证明仿真技术可靠,可为汽车柔性管线的设计和布置提供依据。
关键词:汽车; 柔性管线; Cosserat弹性杆; 动态仿真
中图分类号:TH123; U463.6
文献标志码:B
Motion simulation analysis technology for
automobile flexible pipeline and its application
WEI Congmin ZHANG Sanlei WANG Guangyao WENG Yang
(Technique Center SAIC Motor Co. Ltd. Shanghai 201804 China)
Abstract:
As to the lack of dynamic simulation support for design and layout ofautomobile
flexible pipelines a motion simulation analysis technique for flexible pipelines is proposed based on Cosserat elastic rod theory. The modeling and dynamic simulation analysis are carried out by takingan automobile brake hose
as an example. The motion simulation analysis model is validated by real test. The simulation results are in good agreement with the real automobile test results. It proves that the simulation technology is reliable. It can provide the basis for the design and layout of flexible pipelines for automobiles.
Key words:
automobile; flexible pipeline; Cosserat elastic rod; dynamic simulation
0 引 言
众所周知,汽车的发动机、冷却系统、空调系统、变速箱系统和制动系统等存在大量柔性管线。为保证汽车正常行驶,必须合理布置管线,以避免因干涉、拉脱、过度弯扭等造成管线失效。目前,设计工程师主要依靠经验进行管线设计与布置,通过实车试验进行纠错,效率较低。在设计初期,由于无法对管线动态失效风险进行评估,造成实车试验时管线与周围部件动态干涉的案例较多。在设计后期,若管线需重新布置,会有更多的设计约束条件,难度更大。
近几年,柔性线束的模拟备受国内外学者的关注。LOOCK等[1]提出线缆弹簧模型,可对不同刚度的线缆进行仿真分析,但不能实现复杂拓扑结构的电缆装配仿真。ARBIND等[2]利用最小二乘有限元模型对不可伸长和剪断的Cosserat杆进行瞬态分析。HERMANSSON等[3]提出一种低维路径规划方法,并成功应用于工业测试案例。CAO等[4]研究Cosserat热弹性杆的动力学方程,扩展简单的Cosserat杆模型。王志斌等[5]采用弹簧质点模型方法对线束进行建模,其运动过程是线束的静态位姿在时间轴上的组合。魏发远等[6]采用蛇形机器人方法,分别提出针对刚性组件和柔性线束的建模方法。刘检华等[78]提出以Kirchhoff弹性细杆非线性力学理论为基础的虚拟环境下活动线缆建模与运动仿真方法,对活动线缆的仿真效果较好,但忽略线缆的拉伸变形和应力分布。刘延柱等[911]基于精确Cosserat模型对螺旋杆和Timoshenko梁进行稳定性分析。王发麟等[12]和林海立等[13]提出基于Cosserat弹性杆理论的建模和仿真方法,能够模拟线束的弯曲和扭转变形,对线束的仿真效果较好。
本文在已有研究的基础上,基于Cosserat弹性杆理论,提出汽车柔性管线的运动仿真分析技术,以制动软管为例,进行建模和运动仿真分析,并对比仿真结果与实车试验结果,证明该方法的可靠性。该方法可为汽车柔性管线的设计和布置提供依据。
1 Cosserat弹性杆基础理论
汽车柔性管线为细长的柔性体,在汽车运动过程中,可以认为其本构关系为弹性关系,因此采用Cosserat弹性杆理论对汽车柔性管线进行建模。
1.1 柔性管线空间位姿描述
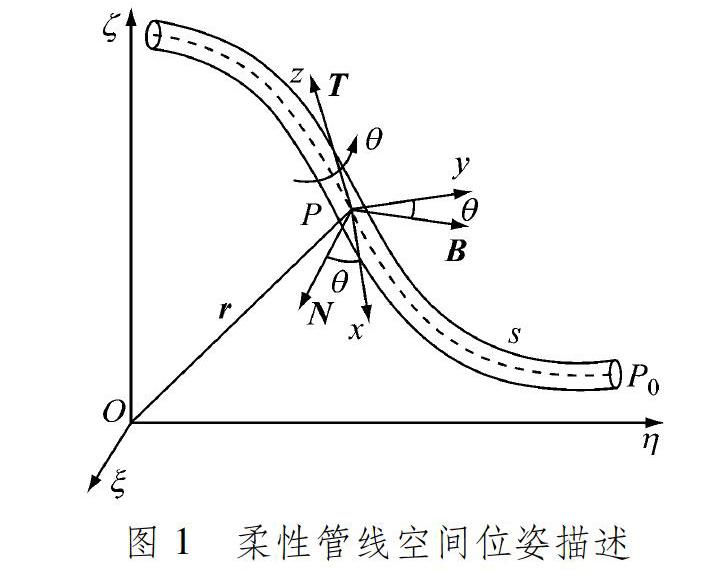
柔性管线的几何形态可由刚性截面沿中心线的移动和转动体现。以中心线上的固定点P0为原点建立弧坐标s,以空间中固定点O为原点建立参考坐标系Oξηζ,O点到空间任意点的向量为r,在曲线上的任意点P可定义一个依附于曲线C的右手坐标系PNBT,称为Frenet坐标系,见图1,其中:T为该点处切线方向的单位矢量,N为该点处法线方向的单位矢量,矢量
B=T×N。在P点建立与刚性截面固连的主軸坐标系Pxyz,其中z轴与P点处的切线T重合。主轴坐标系x轴与Frenet坐标系N轴的夹角为θ,θ即为截面的扭转变形。
1.2 柔性管线参数化模型
设柔性管线中心线为曲线C,选定C上的P0点为起始点,建立沿C的弧坐标s,C上任意点P的位置由s确定。以固定点O为原点,建立线缆参数化模型的固定参考坐标系Oξηζ,见图2。矢径r可确定C上的运动节点P的位置,r为s的单值连续可微函数。
r(s)可确定曲线C的空间几何形状,C在P点处的切线矢量
T可描述为
T(s)=dr(s)
ds(1)
曲线C在P点处的曲率K(s)定义为T对
s的导数的模,即
K(s)=dT
ds(2)
r可确定C上各节点的空间位置,通过求解r即可得到同一时刻线缆中心线C的空间几何形状。r的求解公式为
r(s)=∫s0
T(s)ds+r(0
)
式中:矢径r(0)表示P0点的空间位置。
在Frenet坐标系中,N和B张成的平面(N,
B)称为曲线C在P点处的法平面,记为。引入时间变量t,C在法平面内随时间t的演化可表达为偏微分方程
ct=V·en(4)
式中:V为决定曲线C上各点运动速度的函数;en为法线轴N的基矢量
。随着时间演化,在不同时刻获得相应的线缆空间曲线形状,形成曲线集。
2 汽车制动软管动态仿真模型
2.1 材料模型
汽车制动软管的主要材料性能参数包括弯曲刚度、拉伸刚度、扭转刚度和线密度等,见表1。
2.2 动态仿真模型
基于Cosserat弹性杆理论对某车型前轮制动软管进行建模。汽车悬架、车身和轮胎等结构均设置为刚体,制动软管为柔性体,悬架按照运动副连接。制动软管的外径为5.0 mm,内径为1.6 mm。制动软管简化成截面与中心线正交的模型,形态求解简化为中心线形态的确定。中心线以梁单元进行划分,并赋予弯曲刚度、扭转刚度和拉伸刚度等参数。制动软管的一端固定于车身,另一端采用NODE节点与悬架进行关联,实现与悬架的随动。制动软管的动态仿真模型见图3。
3 动态仿真模型验证
为驗证建模方法的可靠性,当轮胎处于不同状态时,在实车装配和动态仿真建模下对比该车前轮制动软管与驱动半轴的最小间隙,多次采样均值与动态仿真结果的对比及其相对误差见表2。
由表2可知,多次采样均值与动态仿真结果的相对误差均在10%以内,证明此建模方法可靠。此外,造成多次采样均值均小于动态仿真结果的主要原因是实车装配过程存在装配误差。
在车轮不同状态时,实车装配和动态仿真的制动软管走势对比见图4。由此可知,在实际装配与动态仿真下,制动软管的走势几乎完全相同,同样说明该建模方法的可靠性。
(a1)实车装配
(a2)动态仿真
a)回正状态
(b1)实车装配
(b2)动态仿真
b)右极限
(c1)实车装配
(c2)动态仿真
c)上极限+左极限
4 制动软管仿真结果分析
对制动软管的实际运动情况进行模拟,得到制
动软管在运动过程中的最小弯曲半径、最大端部拉力和软管与驱动半轴的最小动态间隙,为制动软管的设计和布置提供依据。制动软管的弯曲半径曲线见图5。由此可知,制动软管的最小弯曲半径为23.2 mm,满足设计要求。
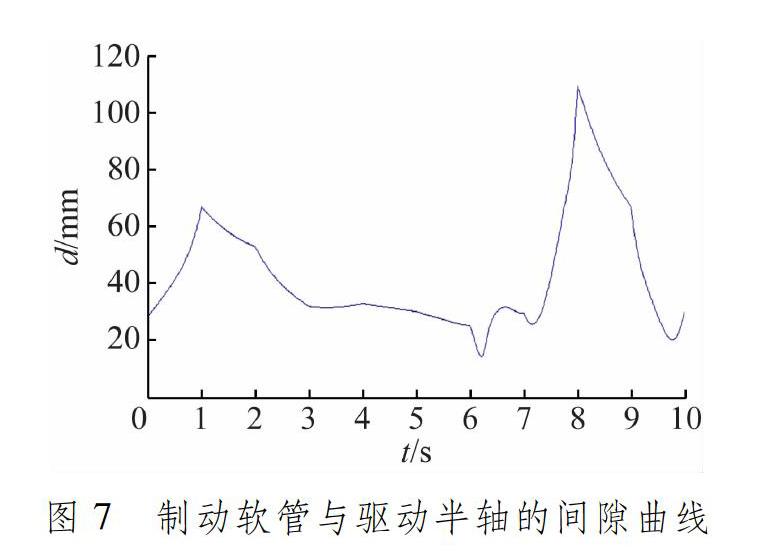
制动软管的端部拉力曲线见图6。由此可知,制动软管的最大端部拉力为19.9 N,满足设计要求,在汽车运动过程中制动软管无拉脱风险。制动软管与驱动半轴的间隙变化曲线见图7。由此可知,制动软管与驱动半轴的最小间隙为14.0 mm,不满足设计要求。在汽车运动过程中,制动软管与驱动半轴有干涉风险,需对制动软管进行优化。
5 结束语
基于Cosserat弹性杆理论的汽车柔性管线运动仿真分析技术具有效率高、可定量研究的特点。本文引入柔性管线的材料机械特性,考虑管线弯曲刚度、扭转刚度、拉伸刚度和自身重力对管线实际走向的影响,可解决柔性管线设计与布置长期缺乏仿真技术支持的问题。
仿真结果与实车试验结果对比可知,管路走向与间隙数值一致性较高,证明仿真方法可靠,可应用于早期整车管线设计和开发,实现在无样车阶段对汽车柔性管线进行动态干涉风险评估,进而指导整车柔性管线设计和布置。
参考文献:
[1] LOOCK A SCHMER E. A virtual environment for interactive assembly simulation: From rigid bodies to deformable cables[C]// Proceedings of 5th World Multiconference on Systemics Cybernetics and Informatics: Emergent Computing and Virtual Engineering. Orlando: International Institute of Informatics and Systemics 2001: 325332.
[2] ARBIND A REDDY J N. Transient analysis of Cosserat rod with inextensibility and unshearability constraints using the leastsquares finite element model[J]. International Journal of NonLinear Mechanics 2016 79: 38 47. DOI: 10.1016/j.ijnonlinmec.2015.10.009.
[3] HERMANSSON T BOHLIN R Carlson J S et al. Automatic assembly path planning for wiring harness installations[J]. Journal of Manufacturing Systems 2013 32(3): 417 422. DOI: 10.1016/j.jmsy.2013.04.006.
[4] CAO D Q SONG M T TUCKER R W et al. Dynamic equations of thermoelastic Cosserat rods[J]. Communications in Nonlinear Science and Numerical Simulation 2013 18(7): 18801887. DOI: 10.1016/j.cnsns.2012.11.011.
[5] 王志斌 刘检华 刘佳顺 等. 面向电缆虚拟装配仿真的多分支弹簧质点模型[J]. 机械工程学报 2014 50(3): 174183. DOI: 10.3901/JME.2014.03.174.
[6] 魏发远 王峰军 陈新发. 含有柔性电缆的复杂系统装配仿真[J]. 工程设计学报 2007 14(1): 2530. DOI: 10.3785/j.issn.1006754X.2007.01.006.
[7] 劉检华 万毕乐 孙刚 等. 线缆虚拟布线与敷设过程仿真技术[J]. 计算机集成制造系统 2012 18(4): 787795.
[8] 刘检华 赵涛 王春生 等. 虚拟环境下的活动线缆物理特性建模与运动仿真技术[J]. 机械工程学报 2011 47(9): 117124. DOI: 10.3901/JME.2011.09.117.
[9] 刘延柱 薛纭. 基于精确Cosserat模型的螺旋杆稳定性分析[J]. 应用数学和力学 2011 32(5): 570578. DOI: 10.3879/j.issn.10000887.2011.05.007.
[10] 刘延柱. 弹性介质中任意形状细长曲梁的Cosserat模型[J]. 工程力学 2014 31(8): 7782. DOI: 10.6052/j.issn.1000 4750.2013.02.0141.
[11] 刘延柱 薛纭. 基于高斯原理的Cosserat弹性杆动力学模型[J]. 物理学报 2015 64(4): 044601. DOI: 10.7498/aps.64.044601.
[12] 王发麟 廖文和 郭宇 等. 基于精确Cosserat模型的柔性线缆物理特性建模与变形仿真技术[J]. 计算机辅助设计与图形学学报 2017 29(7): 13431355.
[13] 林海立 刘检华 唐承统 等. 基于Cosserat弹性杆理论的柔性线缆物理建模方法[J]. 图学学报 2016 37(1): 34 42. DOI: 10.11996/JG.j.2095302X.2016010034.

