向日葵花盘直径及面积的测量
张卫正,殷长魁,金保华,张伟伟,刘 岩,陈启强,蒋珂珂
(郑州轻工业大学,河南 郑州 450002)
向日葵(HelianthusannuusL.)是菊科向日葵属的1年生草本植物,被誉为具有重要经济价值的世界四大油料作物之一[1]。向日葵为头状花序,生长在茎的顶端,俗称花盘。花盘上有2 种花,即舌状花和管状花。舌状花为无性花,着生在花盘边缘1~3层,呈橙黄或淡黄色,具有引诱昆虫前来采蜜授粉的作用。管状花为两性花,位于舌状花内侧,主要生长在圆盘区域,呈黄褐色[2]。
向日葵是典型的异花授粉作物,必须在传粉昆虫或其他生物媒介的作用下才能授粉[3]。向日葵自花授粉结实率极低,仅为3%左右,而异花授粉结实率较高。适时施肥浇水、防治病虫害,以及采取放蜂或人工辅助授粉等措施可提高结实率[4]。已有的研究表明,向日葵花粉、花色、花香、花蜜量和花盘上舌状小花的大小等是吸引蜜蜂等传粉者的重要植物性状[5]。向日葵产量与花盘的大小密切相关,花盘尺寸是估测产量的一个重要指标[6-7]。同时,向日葵的产量还在一定程度上受蜜蜂及人工辅助授粉的影响[8-9]。
将机器视觉和图像处理技术应用于农业研究与生产,具有广泛的应用前景和实用价值。例如,根据植物的视觉差异进行水果与蔬菜的识别[10]、检查和分级蔬菜[11-12],对药用植物叶片进行分类[13],对畜禽生长进行监测[14]等。在向日葵花盘和圆盘等组件的参数测量方面,常用人工方法获取向日葵花盘和圆盘的直径、面积等参数[15-16];而基于图像处理的向日葵植株、叶片及花盘等参数测量的研究较少。郭丽娟[17]根据向日葵种子内部含油率不同,采用近红外技术和计算机视觉技术设计了种子自动分选系统,将种子准确地区分为2 个级别,提高了经济效益。狄鹏慧等[18]以向日葵叶部锈病为主要研究对象,以Matlab为平台,将自然光照条件下采集到的向日葵叶部病害图像进行预处理,再分别利用病斑的颜色及纹理特征,对向日葵叶部病害进行了较准确地识别诊断。越鲜梅[19]以Matlab为平台,利用GUI工具箱开发了基于图像识别的向日葵叶部病害诊断系统,能够较准确地识别出向日葵细菌性叶斑病、黑斑病和霜霉病。DUCOURNAU等[20]开发了用于自动监测向日葵种子发芽率的图像采集系统,将彩色图像转换为二值化图像,进行发芽种子的计数,检测平均发芽时间。ARRIBAS等[21]提出了基于机器视觉和神经网络的向日葵叶片自动分类系统,从分割的图像中提取叶片形态特征,然后以叶片的周长、面积及拟合椭圆长轴、短轴和宽高比作为特征集,最后采用广义感知器神经网络架构与后验概率模型选择算法,确定目标是否为向日葵叶片,正确分类率为85%。
鉴于国内外基于图像处理技术,以向日葵为对象的相关研究较少,且向日葵花盘等的尺寸与对传粉者的吸引力、产量估计密切相关,本研究设计了背景板、遮挡板以及三脚架用于图像采集,通过自动化编程进行向日葵花盘等参数的准确、快速测量,统计分析花盘多个径向的直径,随之获取向日葵花盘、圆盘等的面积、周长等几何参数。所提出的方法具有快速无损、工作量小、精度高等优点,为向日葵产量估计、育种相关的表型研究、传粉媒介的相互作用研究等提供技术支持。
1 材料和方法
1.1 试验材料
本研究选择不同品种的向日葵,直径(水平和竖直方向上直径的平均值)介于90~221 mm。共25个向日葵品种,每个品种5株,共计125株。
1.2 试验装置
在农业领域中获取数字图像容易出现失真、阴影、背景干扰、对比度低、缺乏用于尺寸校正的参照物等问题,从而影响图像处理的效果。针对以上问题,本研究设计了用于向日葵花盘图像采集的背景板及遮挡板,如图1所示。

1:白色背景板;2:狭缝;3:黑色圆形标记物;4:遮挡板;5:双面胶带1:White background board;2:Slit;3:Black circular marker;4:Shielding board;5:Double-sided tape
为了提供对比鲜明的背景,便于后续向日葵花盘图像提取,本研究使用特制的、带有狭缝的白色背景板(大小为600 mm×500 mm,厚度为7 mm)。在板上切割一个狭缝,该狭缝的上端为224 mm×30 mm的矩形,下端是边长为30 mm的正六边形,该正六边形的中心与背景板的中心重合。将4个直径为30 mm的黑色圆形标记物固定在背景板的4个角上,使得4个黑色圆形标记物的圆心连线构成边长为400 mm的正方形。该正方形的中心与背景板的中心重合,该正方形的4条边分别与背景板的4条边平行。这4个黑色圆形标记物起到标记和参照的作用,通过投影的变换来校正图像的失真,以及为计算向日葵花盘等尺寸提供参照比例。
遮挡板大小为220 mm×85 mm,双面胶带大小为220 mm×10 mm,分别位于遮挡板的左右两侧。向日葵的花梗通过狭缝到达背景板中心的正六边形中,此时向日葵的花盘则位于背景板的中心。使用带有双面胶带的白色遮挡板,将遮挡板粘贴在背景板的狭缝上,实现可拆卸式的“封闭狭缝”的功能。
用于固定背景板的便携式三脚架,如图2所示。三脚架高度0.4~3.0 m,满足不同高度的向日葵花盘图像采集的需求。2个抓手用于抓持背景板,其长度可调节。多方位360°可旋转球形云台具有任意调节角度的功能,可以按照试验需求调节背景板的朝向和角度。

1:抓手;2:可旋转球形云台;3:支撑杆;4:一级调节旋钮;5:一级升级杆;6:三脚支撑1:Gripper;2:Rotatable spherical head;3:Support rod;4:One-stage adjustment knob;5:One-stage lifting rod;6:Three-leg support
1.3 图像采集及处理流程
本研究使用便携式平板电脑Surface Pro 4(Windows 10操作系统、Intel Core i7 6650U处理器、16 GB内存)自带的后置相机采集向日葵的图像,并存储为JPEG格式,图像大小为800万像素。平板电脑的相机与向日葵花盘大体位于相同的高度,距离保持在1~2 m,确保背景板上的4个黑色圆形标记物尽量占据相机视场的边缘。图像中只有向日葵的花盘露在白色背景板上,消除了向日葵茎、叶的干扰,减小了花盘图像提取的难度。
单人即可完成装置搭建及图像采集,节省了人力资源。处理流程为,首先将向日葵的花盘调整到背景板的中心,并粘贴遮挡板,保证背景板上只有向日葵花盘;然后放置三脚架,用抓手固定背景板并调整朝向,采集图像;接着进行图像处理,将所采集的向日葵花盘图像进行二值化处理;然后对二值化图像进行裁剪,获得保留4个黑色圆形标记物的图像;之后检测这4个黑色圆形标记物,并分别提取其坐标;根据4组对应点确定投影变换的参数,并进行投影变换;在HSV颜色空间提取花盘,采用纹理分割及开运算、闭运算等形态学操作获取圆盘;然后提取花盘的凸壳,采用尖端包裹法分别提取花盘、圆盘的尖端轮廓;逆时针方向分别按照像素行进法和等角度采样法计算不同采样次数的花盘、圆盘的平均直径,并确立平均直径的预测模型;最后计算向日葵花盘、圆盘的面积、周长、等效直径、拟合椭圆的长轴和短轴的长度。所有图像处理均在Matlab开发的应用程序中完成。
1.4 图像二值化及裁剪
通过平板电脑的摄像头获取向日葵花盘的原始图像,如图3a所示。采用Matlab软件中的函数rgb2gray(),将原始图像转换为灰度图像。采用函数graythresh()获得将灰度图像转换为二值化图像所需的阈值yz。结合阈值yz,采用函数im2bw(),将灰度图像转换为二值化图像,如图3b所示。
从图3a可知,向日葵花盘图像中背景板的左右两侧有叶片、建筑物及其他物体的干扰,需要将其裁剪掉,保留背景板中4个黑色圆形标记物所包围的区域。从图3b可看出,背景板的左右两侧区域出现黑色像素,而背景板的左右两侧靠近边缘的部分是白色区域。
从图3b的最左侧的第一列开始,连续出现40个列的所有像素值之和大于(40×m-120)(m为图像的行数),则认定该连续40列的中值为左侧起始列。从图3b的最右侧的列开始,向左行进,如果连续出现40个列的所有像素值之和大于(40×m-120),则认定该连续40列的中值为右侧终止列。将图3b起始列到终止列范围内的像素值保存,如图3c所示。将图3a起始列到终止列范围内的像素值保存,如图3d所示。实现了图像的裁剪,保留了目标区域。

a:原始图像;b:二值化图像;c:裁剪后的图像;d:裁剪后的彩色图像
1.5 黑色圆形标记物检测及其坐标中心提取
为了进行图像投影变换,最大程度地减小相机的畸变,将图像的各个像素点恢复到理想位置,需要提取图3d中4个黑色圆形标记物的中心位置(质心)的坐标。
通过Matlab中的函数size()获取图3d的大小,并设定其共有cjm行、cjn列。本研究设定图3d左上角、右上角、右下角、左下角的黑色圆形标记物分别为bjw1、bjw2、bjw3、bjw4。
将图像中1~(cjm×0.2)行的像素值存储到ashangsh中,将图像中(cjm×0.8)~cjm行的像素值存储到axiash中。如果cjm×0.2、cjm×0.8不是整数,采用Matlab中的取整函数floor()进行取整操作。
1.5.1 提取ashangsh中2个黑色圆形标记物的质心坐标 采用Matlab中的函数bwlabeln对ashangsh进行连通区域标记,得到矩阵lts;采用函数max(max(lts))得到图像ashangsh中连通区域的总数量ltszs。采用Matlab中的函数regionprops()获得各个连通区域面积(即像素数)的数组STATSs;采用STATSs().Area将各个连通区域的面积存储到getmianjis(i)中,其中,i的值为1~ltszs,分别对应1~ltszs个连通区域的面积。
第一步:采用Matlab中的函数find()查找面积最大的连通区域,并将该连通区域在矩阵lts的位次值存储到zuidas。
第二步:采用Matlab中的函数regionprops()计算各个连通区域的质心,将表示各个连通区域质心的坐标存储到数组zhixins,则zhixins(zuidas)表示上端2个黑色圆形标记物之一的中心坐标。
第三步:如果zhixins(zuidas)的列坐标大于0.5×cjn,则判定zhixins(zuidas)表示右上角黑色圆形标记物bjw2质心的坐标,否则判定zhixins(zuidas)表示左上角黑色圆形标记物bjw1质心的坐标。
将矩阵lts中的值为zuidas的元素全部置0,然后采用上述方法的第一步和第二步,得到上端2个黑色圆形标记物之一的中心坐标zhixins(zuidas2)。如果zhixins(zuidas)表示右上角黑色圆形标记物bjw2质心的坐标,则zhixins(zuidas2) 表示左上角黑色圆形标记物bjw1质心的坐标;如果zhixins(zuidas)表示左上角黑色圆形标记物bjw1质心的坐标,则zhixins(zuidas2) 表示右上角黑色圆形标记物bjw2质心的坐标。
1.5.2 提取axiash中2个黑色圆形标记物的质心坐标 采用与1.5.1中相同的方法,对axiash进行分析,得到zhixinx(zuidax)表示左下角黑色圆形标记物bjw4质心的坐标,zhixinx(zuidax2)表示右下角黑色圆形标记物bjw3质心的坐标。4个黑色圆形标记物全部检测并标记出来,如图4所示。其中,如果zhixinx(zuidax)的列坐标大于0.5×cjn,则判定zhixinx(zuidax)表示右下角黑色圆形标记物bjw3质心的坐标,否则判定zhixinx(zuidax)表示左上角黑色圆形标记物bjw4质心的坐标。

图4 黑色圆形标记物检测及标记
1.6 图像投影的变换
本研究展示了基于4组对应点进行的投影变换,以校正所采集图像的失真,如图5所示。4个黑色圆形标记物的质心用作投影变换的参考点,并以相邻2个黑色圆形标记物的距离400 mm作为参考标尺。
执行投影变换时,将经过校正的理想图像的目标点bjw1′、bjw2′、bjw3′、bjw4′的坐标作为输入,设定其质心的坐标分别为(yx1,yy1)、(yx2,yy2)、(yx3,yy3)、(yx4,yy4)。将图3d的标记点(与图3c的标记点相同)bjw1、bjw2、bjw3、bjw4的坐标作为输出,设定其质心的坐标分别为(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)。yx1的值为1,yy1的值为1,yx2的值为1,yy2的值为3 000,yx3的值为3 000,yy3的值为3 000,yx4的值为3 000,yy4的值为1;从而保证投影变换后的图像的大小为3 000×3 000像素。

I:裁剪后的图像;I′:经过投影变换、适合于测量的图像
根据投影变换的原理,存在如下关系式:
DY=M×A
(1)
A=[jza11;jza12;jza13;jza21;jza22;jza23;jza31;jza32]
(2)
DY=[x1;y1;x2;y2;x3;y3;x4;y4]
(3)

(4)
其中,DY表示由裁剪图像的4个黑色圆形标记物的质心坐标构成的坐标矩阵,M表示投影变换矩阵,A表示变换参数,包含公式(2)中所设定的8个元素,可通过已知参数求解出来。
将图3d的黑色圆形标记物bjw1、bjw2、bjw3、bjw4质心的坐标、目标点bjw1′、bjw2′、bjw3′、bjw4′的坐标代入公式(1)—(4),解算出A中各元素的值[22]。
根据公式(1)计算出图像I′中每个像素点的坐标对应于图3d中的坐标。如图6所示,原始图像与目标图像之间的对应点关系,坐标可能不是正好落在光栅点上,需要进行像素值的插值,确保图像像素值的准确性和连续性。

图6 原始图像与目标图像之间的对应点Fig.6 Corresponding points between the originalimage and the target image
本研究采用双三次插值法(Bicubic interpolation)进行图像插值。在该方法中,函数f在点(x,y)的值可以通过矩形网格中最近16个采样点的加权平均得到。需要使用2个多项式插值三次函数,每个方向使用1个。不仅考虑到4个直接相邻点的灰度影响,还需考虑到各相邻点间灰度值变化率的影响。双三次插值是更加复杂的插值方式,能创造出比双线性插值更平滑的图像边缘[22]。
构造Bicubic函数:
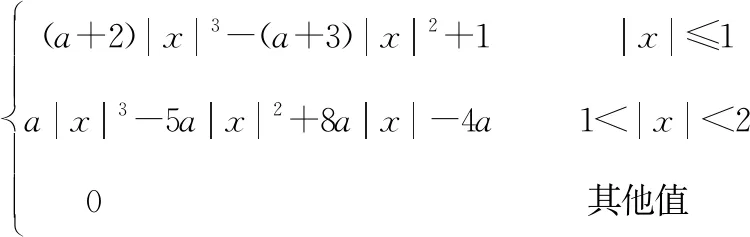
(5)
其中,a取-0.5。对待插值的像素点(x,y)(x和y可以为浮点数),取其附近的4×4邻域点(xi,yj)。其中,i= 0、1、2、3,j=0、1、2、3。按如下公式进行插值计算:
(6)
计算出I′中的(i,j)处的点对应的在裁剪图像I中的位置为(cjwzX,xjwzY)。像素点(cjwzX,xjwzY)最近的16个像素点的加权平均作为I′中的(i,j)处的像素值。依次计算完成I′中的3 000×3 000个坐标处像素点的值,采用公式(5)—(6),实现了坐标图像的投影变换及像素插值,并将I′设定为图像tybh,如图7所示。
投影变换通过使用4个黑色圆形标记物质心,将所识别的尺寸标记映射到目标坐标来校正图像失真,并且该映射在投影变换过程中校正了整个图像。
1.7 花盘图像的提取
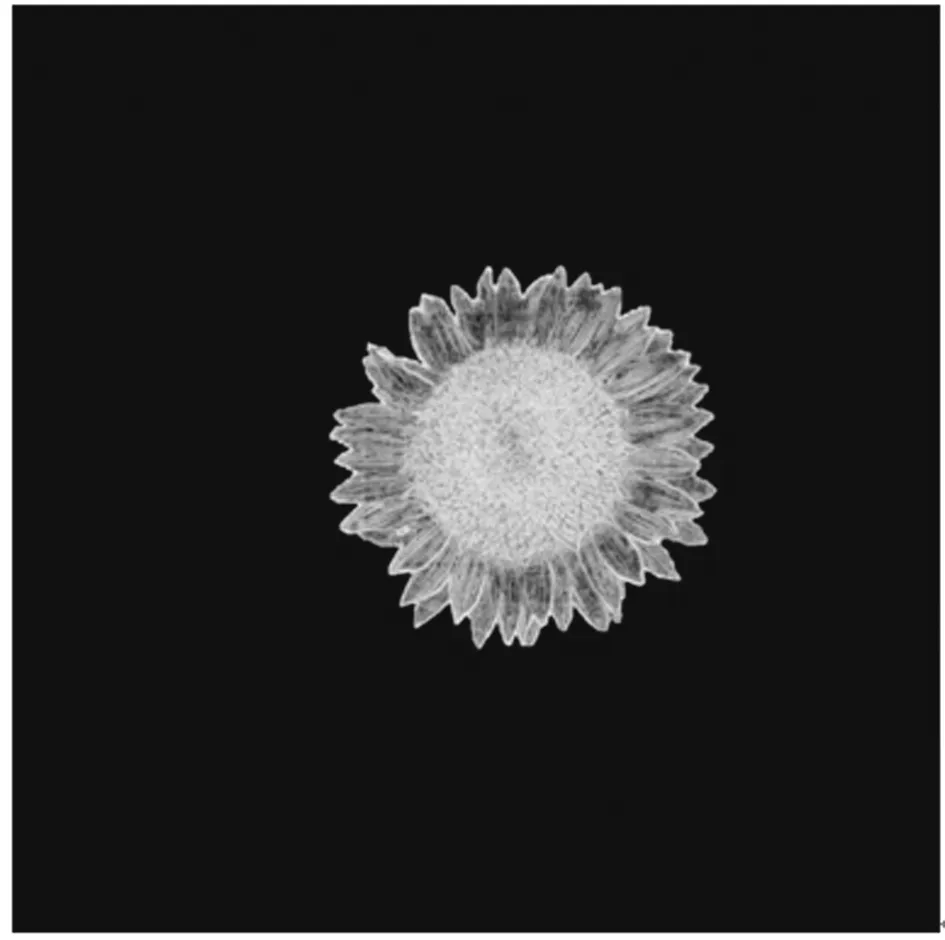
对经过投影变换得到的图像tybh进行向日葵花盘图像的提取,花盘的外部轮廓由1~3层的黄色舌状小花包围,圆盘中的区域也显示黄色或接近黄色,所以本研究采用提取黄色的方法对花盘图像进行提取。

图7 经过投影变换的图像
首先采用Matlab中的函数rgb2hsv()将该图像转换为hsv_f,从而分别得到图像的色调(H)、饱和度(S)和明度(V)。对hsv_f的每个像素进行逐一判断,是否满足公式(7)。
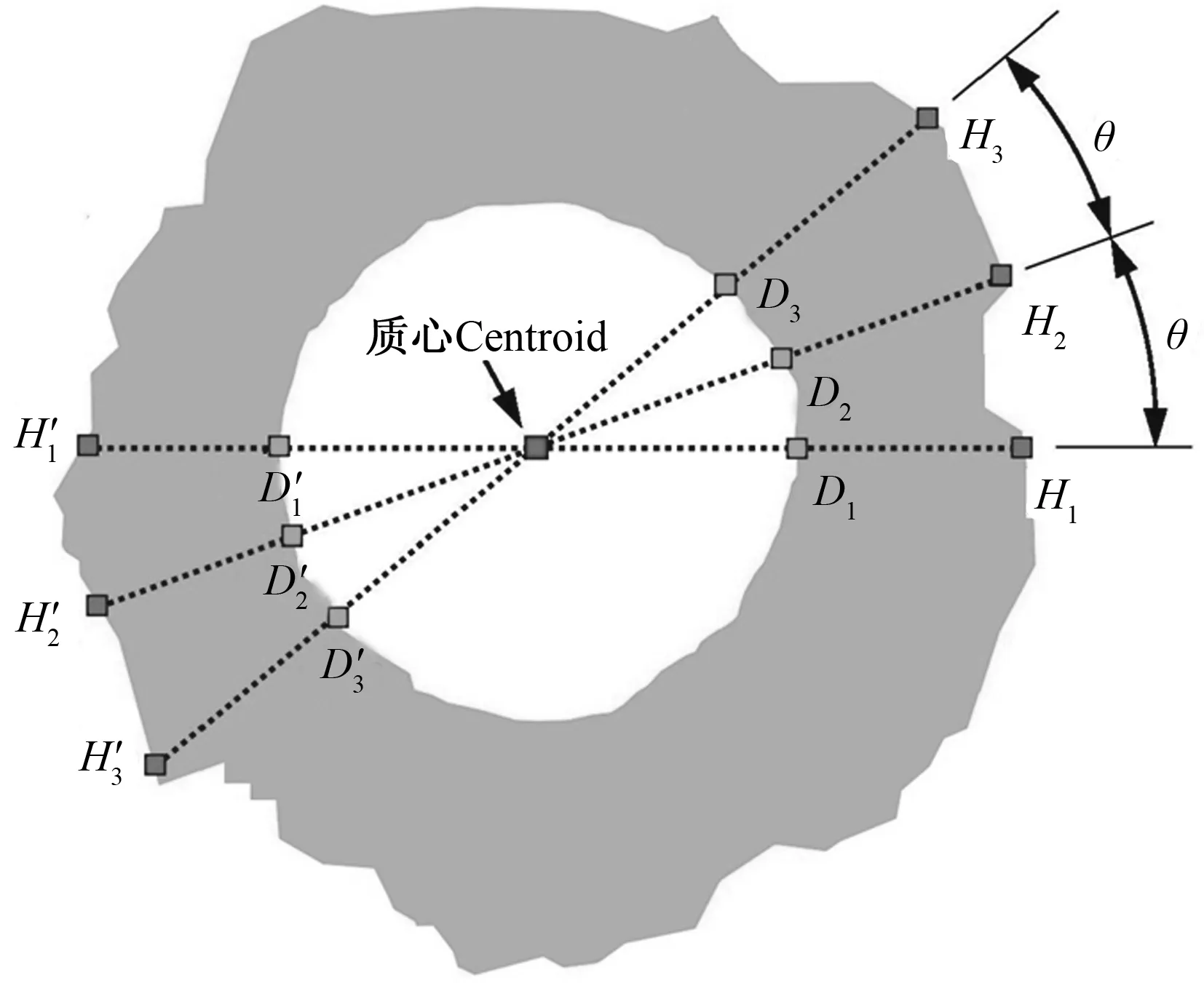
26 (7) 如果满足,则设定该点的值为1,否则为0,从而得到二值化图像hfl,如图8a所示。如果hfl(i,j)的值为1,表示图像tybh中的像素点(i,j)为黄色;如果hfl(i,j)的值为0,表示图像tybh中的像素点(i,j)不是黄色。 采用Matlab中的函数imfill(hfl,‘holes’)对二值化图像hfl进行孔洞填充,得到图像8a,并采用Matlab中的函数bwareaopen(a8,100)对图像8a进行小面积去除(其中,100表示对面积小于100个像素的区域进行删除),消除噪声干扰,保留唯一的花盘区域,得到图8b。 采用图8b对图像tybh进行掩模得到图8c,从而保留了图像tybh中的花盘区域,图8c中的其他区域全部为黑色,实现了对向日葵花盘图像的提取。 a:二值化图像;b:去除孔洞的图像;c:保留花盘的图像 花盘外部轮廓的舌状小花和花盘中部圆盘的颜色相近,给圆盘的分割和提取造成严重干扰。常用的颜色阈值、灰度阈值等方法不能较好地实现圆盘图像的分割和提取。舌状小花每个花瓣的边缘呈直线或弧线等线状纹理,较长且窄;舌状小花的花瓣中间区域较为平滑,纹理较少。而圆盘是向日葵种子聚集的区域,呈现较为密集的点状纹理。本研究采用纹理分割的方法提取圆盘。 采用Matlab中的函数entropyfilt()对图8c进行处理,得到纹理图像wenli,如图9所示。由于图8c为RGB三通道组成的图像,对其进行纹理分析得到的图像wenli也是三通道图像。 图9 向日葵花盘的纹理图像 采用Matlab中的函数mat2gray()将图像wenli转换为灰度图像Eim。然后采用Matlab中的函数im2bw(Eim,0.7),以0.7作为阈值将灰度图像Eim转换为二值化图像EIM2,如图10a所示。 a:向日葵花盘纹理图像的二值化;b:面积最大的连通区域的图像;c:孔洞填充后的图像;d:开运算后的图像;e:闭运算后的图像;f:提取向日葵圆盘图像 最大连通区域保存方法:采用Matlab中的函数bwlabeln()对二值化图像EIM2进行连通区域标记,并连通各个区域的面积,将二值化图像EIM2中面积小于最大连通区域面积的区域删除,保留了面积最大的连通区域,如图10b所示。 采用Matlab中的函数imfill()对面积最大的连通区域进行孔洞填充,如图10c所示。然后采用Matlab中的函数imopen()进行开运算,如图10d所示。其中,该开运算采用的结构参数是半径为10的圆形结构。开运算平滑了对象的轮廓,断开了狭窄的连接,去掉了细小的突出部分。 再次采用之前建立的最大连通区域保存方法,保留二值化图像10d中的最大连通区域,并存储到EIM5。采用Matlab中的函数imclose(EIM5,sejgtb)对EIM5进行闭运算,得到EIM6,如图10e所示。其中,sejgtb=strel(‘faceplate’,12),表示通过Matlab中的构造函数strel()建立半径为12的圆盘。将提取得到的圆盘区域以红色显示,如图10f所示。 舌状小花环绕圆盘分布,构成了向日葵花盘的外部轮廓,每个舌状小花都可能会产生尖端点,相邻的舌状小花间大多会产生凹陷。花盘不同径向的直径可能落在舌状小花的尖端或凹陷处,一般期望表示直径的2个端点是“尖端到尖端”。所以需要进行多个径向花盘的直径测量,尽量减少差异。为了有效地解决这个问题,本研究提出了尖端包裹法。 尖端包裹法可以被认为是一种收缩包裹类型的几何外壳,包括所有查找到的舌状小花的尖端点。花盘凸包所构成的凸包多边形将覆盖一些舌状小花的尖端点,增加了花盘的面积,并且沿多个径向测量的花盘直径将过高。本研究所提出的尖端包裹法相对于常用的凸包法,更精确地描述了花盘的范围,花盘的直径计算更精准,减小了原来花盘直径较大的起伏变化。采用尖端包裹法所确立的花盘区域进行花盘的直径检测,可以根据等角度采样法提取花盘的直径,求取平均值作为花盘的直径,相对于像素行进(计算所有原始花盘的直径)并求平均值的方法,本研究的计算量更小。 尖端包裹法可以执行多达上千次的不同径向的向日葵花盘直径的测量,可以在进行测量之前设定花盘、圆盘直径测量的采样间隔角度。 第一步:获取花盘的轮廓点。将构成花盘外部轮廓的像素点坐标,按照顺时针方向依次存储起来;按照顺时针方向查找到的外部轮廓像素点的坐标,依次存储到数组结构体boundary1中。将轮廓点显示出来,如图11所示。 第二步:提取花盘的质心坐标点。采用Matlab中的函数regionprops(a99,‘Centroid’)提取花盘的质心的坐标,并设定x坐标为zhixinxzuobiao,y坐标为zhixinyzuobiao。 第三步:提取花盘的尖端点并顺时针连接构成尖端轮廓。依次计算花盘的质心到轮廓上各个点的距离,并储存到数组bianjiezxjuli中。如果轮廓上的任一点Pqd(起点)的前20个及后20个轮廓点到质心的距离都小于Pqd到质心的距离,则认定该Pqd为尖端点,存储尖端点的坐标。遍历花盘轮廓点进行尖端点的查找,并依次存入花盘尖端点的数组jianduan中。查找结果如图12a所示,以圆圈表示各个尖端点。将所有的尖端点依次连接,构成花盘的尖端轮廓,并将该轮廓内的所有像素点置1,存储为jdlk,构成具有尖端轮廓的花盘,如图12b所示。 图11 向日葵花盘的外部轮廓点 a:尖端点查找;b:尖端轮廓 采用Matlab中的函数regionprops(bwlabel(a99),‘ConvexHull’)提取花盘的凸包,并将表示花盘凸包点的坐标存储到结构体数组hpstats,通过hptn=hpstats.ConvexHull,实现花盘的凸包点存储到数组hptn。将数组hptn中的凸包点依次连接,如图13a所示。将凸包轮廓所包围的区域全部置1,并存储到hptk,如图13b所示。 采用同样的方法查找圆盘的尖端点,依次存入数组ypjianduan中,然后连接尖端点构成圆盘的尖端轮廓ypjdlk。查找圆盘的凸包点,将圆盘的凸包点存储到数组yptn,构造圆盘的凸包轮廓yptk。 a:尖端点所构成的凸包轮廓;b:凸包轮廊所包围的区域 从图14可以看出,基于向日葵花盘原始轮廓和尖端轮廓分别进行多个径向的直径测量。设定圆盘的质心与之前计算得到花盘的质心相同,线段H1H1′与D1D1′重合,且都经过质心,点H1、H1′位于花盘的轮廓上,点D1、D1′位于圆盘的轮廓上。将所需的测量次数(n)作为输入,并且沿每个角度间隔θ(θ=180°/n)进行测量。本研究中,n分别为2、4、8、16、32、64、128、180。分别计算n次测量后直径的平均值。实现了花盘尖端轮廓等间隔采样的直径测量,采用同样的方法实现圆盘尖端轮廓等间隔采样的直径测量。 图14 向日葵花盘和圆盘直径的测量 选择不同方法、次数进行向日葵花盘直径测量,并观察其对平均直径的影响。测量次数分别设定为2、4、8、16、32、64、128、180,向日葵花盘平均直径如表1、2所示,并分别画出其走势,如图15a、b所示。无论花盘的大小如何,由于采样次数不同,同一株向日葵花盘的平均直径都存在变化。尖端包裹法测量的花盘平均直径大于原始轮廓法,但尖端包裹法测量花盘直径的变化小于原始轮廓法。 如图15a、b所示,当测量次数小于一定次数时,单个向日葵花盘平均直径的变化趋势是随机的。这种随机变化是由于舌状小花的不规则排列引起的。因为基于原始轮廓法测量的花盘直径由尖端到尖端、尖端到凹陷等多种情况构成。在计算花盘尖端轮廓的直径时,由于尖端包裹法填充了部分外部轮廓的凹陷,仅允许连接尖端到尖端,导致直径的变化较小。随着测量次数的增加,平均直径的变化逐渐变小。当测量次数分别大于32、16次时,基于原始轮廓法、尖端包裹法测量的花盘平均直径变化趋于平缓。 表1 基于原始轮廓法测量的向日葵花盘平均直径 表2 基于尖端包裹法测量的向日葵花盘平均直径Tab.2 The average diameter of sunflower faceplate measured by tip wrapping method cm a:基于原始轮廓法测量的向日葵花盘平均直径;b:基于尖端包裹法测量的向日葵花盘平均直径;c:基于原始轮廊法测量的向日葵花盘平均直径的平均绝对偏差;d:基于尖端包裹法测量的向日葵花盘平均直径的平均绝对偏差a:The average diameter of the sunflower faceplate measured based on the original contour method;b:The average diameter of the sunflower faceplate measured by the tip wrapping method;c:The average absolute error of the average diameter of the sunflower faceplate measured based on the original contour method;d:The average absolute error of the average diameter of the sunflower faceplate measured by the tip wrapping method 进行数据分析以评估基于尖端包裹法和原始轮廓法测量的向日葵花盘平均直径的效果,通过绝对偏差公式(8)计算以上2种方法测量直径的平均绝对偏差(Ad)。 (8) 其中,Di是采样次数为i的花盘平均直径(i= 2,4,8,16,32,64,128,180),Dxz是像素行走法测量的花盘平均直径。 如图15c、d所示,使用不同的采样次数测量的花盘平均直径与像素行走法测量的花盘平均直径进行对比,提供了由测量次数产生偏差的清晰变化。基于尖端包裹法所测量的花盘平均直径的平均绝对偏差相对低于原始轮廓法。虽然测量次数不同,向日葵花盘平均直径的平均绝对偏差不同,但很明显,增加测量次数会降低平均绝对偏差,使其逐渐收敛并接近0。其中,D180已经非常接近Dxz,两者的绝对偏差为0.06%。 建立基于原始轮廓法测量花盘平均直径(HOD)的预测模型。 HOD=-1.24+0.992×HOD2 (9) 其中,HOD2表示原始轮廓法2次采样测量的花盘平均直径。HOD与HOD180(180次采样测量的花盘平均直径)决定系数R2=0.997。 建立基于尖端包裹法测量花盘平均直径(HTD)的预测模型。 HTD=2.813+1.051×HTD2 (10) 其中,HTD2表示尖端包裹法2次采样测量的花盘平均直径。HTD与HTD180(180次采样测量的花盘平均直径)决定系数R2=0.991。 建立基于原始轮廓法测量圆盘平均直径(DOD)的预测模型。 DOD=-0.128+0.997×DOD2 (11) 其中,DOD2表示原始轮廓法2次采样测量的圆盘平均直径。DOD与DOD180(即180次采样测量的平均直径)决定系数R2=0.998。 建立基于尖端包裹法测量圆盘平均直径(DTD)的预测模型。 DTD=-0.991+1.024×DTD2 (12) 其中,DTD2表示尖端包裹法2次采样测量的圆盘平均直径。DTD与DTD180(即180次采样测量的平均直径)决定系数R2=0.999。 从关系式(9)—(12),以及预测模型的决定系数可知,本研究所建立的预测模型的精度高,计算量小(仅以2次采样测量的平均直径代入预测模型,就可以高精度地预测180次采样的平均直径)。 采用Matlab中的regionprops()函数,属性值采用‘Area’,计算所标记区域的像素总个数,也可以认为是标记区域的面积。分别获取花盘原始轮廓所包围区域的面积、花盘尖端轮廓所包围区域的面积以及圆盘的面积。采用Matlab中的regionprops()函数,属性值采用‘Perimeter’,计算所标记区域的周长。分别获取花盘的原始轮廓、尖端轮廓以及圆盘的周长。采用Matlab中的regionprops()函数,属性值采用‘EquivDiameter’,计算与区域具有相同面积的圆直径。采用Matlab中的regionprops()函数,属性值分别采用‘MajorAxisLength’、‘MinorAxisLength’,计算与区域具有相同标准二阶中心矩的椭圆长轴、短轴长度(像素意义下),分别获取花盘的原始轮廓所包围区域、花盘的尖端轮廓所包围区域及圆盘的长轴、短轴长度。 如图16所示,在进行人工测量时,沿着水平和垂直方向测量花盘的长度(EW)和宽度(NS)。比较拟合椭圆直径与(EW+NS)/2的相关性高达0.999,表明本研究测量的精度极高,满足科研和生产的需求。 尖端包裹法增加了向日葵花盘所包围的区域。平均而言,花盘尖端轮廓所包围的面积比原始轮廓所包围的面积增加了13.2%,圆盘尖端轮廓所包围的面积比原始轮廓所包围的面积增加了3.1%。 向日葵花盘尖端轮廓减小了边界的粗糙度,因此其周长明显小于原始轮廓的周长。由尖端包裹法产生的花盘尖端轮廓周长相比原始轮廓法下降了38.2%,由尖端包裹法产生的圆盘尖端轮廓周长相比原始轮廓法下降了10.3%。尖端包裹法填充了舌状小花之间的凹陷,从而使其“更加充实”。 a:人工测量花盘的直径,及用椭圆拟合法获得长轴和短轴的长度;b:人工测量圆盘的直径,及用椭圆拟合法获得长轴和短轴的长度a:The diameter of the faceplate measured manually,the length of the major and minor axes obtained by ellipse fitting;b:The diameter of the disc measured manually,the length of the major and minor axes obtained by ellipse fitting图16 人工测量的花盘和圆盘直径,及用椭圆拟合法获得长轴和短轴的长度Fig.16 The faceplate and disc diameters measured manually,and the length of the major and minor axes obtained by ellipse fitting 对于向日葵花盘和圆盘,人工测量的原始轮廓和尖端轮廓所包围的面积与本研究所计算的原始轮廓和尖端轮廓所包围的面积显示出高度相关性,相关系数为0.97~1.00,这也说明以预测模型进行面积等参数估计具有高度的相关性和可靠性。 根据以上关系,建立向日葵花盘原始轮廓所包围区域的面积(HOA)的预测模型。 HOA=-16 615.19+219.13×HOD2 (13) 其中,HOD2表示基于原始轮廓法2次采样测量的花盘平均直径。HOA与采用Matlab中的regionprops()函数所计算花盘原始轮廓所包围面积的决定系数R2=0.935。 建立花盘的尖端轮廓所包围区域的面积(HTA)的预测模型。 HTA=-18 341.72+247.93×HTD2 (14) 其中,HTD2表示基于尖端包裹法2次采样测量的花盘平均直径。HTA与采用Matlab中的regionprops()函数所计算花盘尖端轮廓所包围面积的决定系数R2=0.942。 由DOD2预测圆盘原始轮廓所包围区域的面积(DOA);由DTD2预测圆盘尖端轮廓包围区域的面积(DTA);其预测结果与采用Matlab计算得到的值的相关性均低于0.65,不具有可靠性。 从关系式(13)—(14),以及预测模型的决定系数可知,本研究所建立的花盘尖端轮廓和原始轮廓所包围区域面积的预测模型精度高、计算量小(仅以2次采样测量的平均直径代入预测模型,就可以高精度预测相关面积)。 本研究开发算法的所有计算都是基于图像像素点构成的矩阵,将其转换为物理单位(以mm为单位),4个黑色圆形标记物的质心构成的正方形边长为400 mm。由于经过投影变换的图像大小为3 000×3 000像素,相当于0.133 mm/像素的测量精度,向日葵花盘和圆盘尖端轮廓、原始轮廓表示直径的数值均需乘以0.133 mm,得到实际的长度;表示向日葵花盘和圆盘尖端轮廓、原始轮廓面积的数值均需乘以(0.133 mm)2,得到实际的面积。该变换消除了由于物体到相机距离的变化而导致的图像分辨率的不一致。该应用程序可在便携式平板电脑中进行分析,用时小于10 s,满足科研和生产的要求。 通过多个品种、不同大小向日葵花盘的试验验证表明,本研究采用的尖端包裹法具有计算量小,对尺度变化不敏感,精度能达到科研和生产要求的优点,具有一定的实用性。本研究所采用的三脚架、背景板和平板电脑等具有一定的便携性,便于在现场使用,并且可自动提供即时的测量参数,人工工作量小;图像处理方法快捷有效,能精确计算向日葵花盘和圆盘的直径、面积等几何参数,有助于理解花卉形态;为衡量向日葵花盘、圆盘等组件和传粉媒介(蜜蜂等)访问率之间相关性提供了技术支撑;通过调整相关参数,本研究所提出的方法可扩展到其他菊科植株花朵的测量与分析;可在本研究的基础上进行后续的花盘中种子数量的统计,便于估计产量、探讨花盘尺寸与产油量之间的关系等。 向日葵的花盘尺寸是评估对蜜蜂等传粉媒介的吸引力和估计产量的重要参数。目前人工测量向日葵花盘相关组件尺寸的方法,耗时耗力、重复性差。因此,本研究提出了图像处理的方法,可以快速无损地获取向日葵花盘、圆盘等的精确尺寸。通过特制的背景板和遮挡板,在现场非破坏性地采集向日葵图像,自动进行图像的投影变换。采用本研究所提出的尖端包裹法确立花盘的范围,通过测量向日葵花盘多个不同径向的直径,确立向日葵花盘的平均直径。通过形态学的开运算和闭运算等操作,确立圆盘的区域并计算直径。结果表明,当花盘直径测量的采样次数为32 次时,直径计算的精度和速度达到较佳的平衡状态;向日葵花盘和圆盘直径的预测模型、花盘面积的预测模型决定系数较高。可见,本研究所提出的图像处理方法具有测量精度高、速度快、对尺度变化不敏感的优点,为研究传粉媒介相互作用提供了技术支持,也适用于其他菊科植株的花朵的测量。
1.8 圆盘图像的提取

1.9 花盘、圆盘尖端轮廓图像的提取



1.10 花盘、圆盘直径的测量
2 结果与分析




3 结论与讨论

