基于颗粒阻尼的PCB动力学与电路联合设计研究
肖望强,余少炜,林昌明,刘利杰
(1.厦门大学 航空航天学院,福建 厦门 361000;2.北京华航无线电测量研究所,北京 100013)
为满足我国空天作战概念的创新,导弹武器正向跨域化、高速化、多用化方向发展。导弹的电子系统能够实现导航、通信、目标识别、跟踪定位等为一体化多功能技术,一旦内置的电子设备出现故障,造成导弹的失误,将会产生灾难性的后果。PCB(Printed Circuit Board)是导弹电子设备的重要组成部分,图1为PCB在导弹中的应用,在导弹受到发射阶段的高强度振动和冲击下,导弹内电子组件会产生严重的动态响应。据统计,在机械力,电磁力,环境等造成电子设备失效的因素中,27%是振动因素造成的[1-2]。传统的减振措施有很多,应用较广的减振元件一般采用橡胶隔震器。但橡胶隔震器存在以下问题:工作温度范围较窄;隔断热传导路径,带来热设计困难;橡胶材料容易老化,需要定期更换等[3-5]。为解决橡胶减振器的弊端,适应未来产品发展需求,急需开发设计一种不隔断传热路径,适用温度范围广,适用频带宽,不引入直线位移和角位移的新型减振技术。

图1 电路板在导弹中的应用Fig.1 Application of circuit board in missile
颗粒阻尼技术是一项振动被动控制的新技术,该技术能够在高低温、辐射等恶劣环境下提供有效的宽频减振,并具有减振效果显著、各向同性、不增加线位移、可靠性高、不改变原结构等诸多优点[6-10]。将颗粒阻尼应用在PCB上,通过颗粒在腔壁中的摩擦与碰撞将动能耗散为热能[11-15],能有效的减少其在运输与使用过程中振动与冲击的影响。
传统的PCB设计一般只考虑电路板图形的布线密度、导线精度等问题,但没有过多考虑电路板的振动问题。因此,本文提出一种新型PCB动力学与电路联合设计方法,这种联合设计的核心就是在电路设计之前先进行动力学分析,确定电路板的振动敏感区域,通过敏感点进行阻尼器的设计和阻尼颗粒参数的优化,最终完成电路体系的设计。本文的联合设计的方法能达到有效的减振效果,特别对于导弹、舰艇的PCB在恶劣振动环境下具有十分重要的理论意义和工程价值。
本文基于PCB动力学特性进行分析,确定阻尼器的安装区域并在非敏感区域设计电路,在敏感区域安装颗粒阻尼器。通过离散单元法计算颗粒的系统耗能,优化颗粒的粒径大小、填充率等参数,提出有效的减振方案。通过与PCB试验相结合的方法,研究颗粒阻尼的配置方案对PCB运动特性的影响规律。
1 PCB的动力学设计
1.1 模型建立
PCB的组件主要由电路板和电子元器件经由机械与电气连接成为一个整体,结构较为复杂。基于本文研究,针对计算模型进行简化,忽略PCB上的元器件对PCB的刚度与质量影响,将其视为薄板处理并删除无关紧要的非承载结构。PCB的尺寸为192×179×2(mm),材料为FR- 4,密度为1.9×103kg/m3,弹性模量为1.11×1010Pa,泊松比为0.28,三维模型如图2所示。
基于ANSYS有限元软件,模型采用实体单元SOLID185,用于构造三维固体结构,把特性参数赋予PCB各部分并划分网格后,建立的有限元模型如图3所示。

图2 电路板三维模型Fig.2 Circuit board three-dimensional model

图3 有限元模型Fig.3 Finite element model
1.2 模态分析
本文针对PCB的联合设计构想,先根据机箱尺寸与元器件的规格确定PCB的尺寸,通过有限元方法确定PCB的模态敏感点区域。模态参数为结构动力特性的优化设计提供依据[16-17],为实现下一步PCB的电路设计奠定基础。由lagrange方程可得一个n自由度的系统运动方程为

(1)
式中:[M],[C],[K]分别为系统质量、系统阻尼和系统刚度矩阵;{F(t)}为外激励矩阵。由于阻尼对系统的固有频率和主振型影响很小,因此可考虑为无阻尼系统,其自由振动方程为
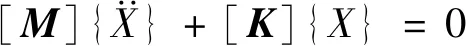
(2)
其特征方程为
(K-ω2M)X=0
(3)
解式(3)可得到系统的第i阶固有频率ωi与第i阶的位移Xi。
基于分机壳体(见图4),使得PCB约束为四周固定方式,在有限元软件中进行模态分析。低阶模态能量占比大,因此对于本文而言,选取图5的一阶弯曲模态,图6、图7的二阶弯曲与三阶扭转模态。图中的条状图表示了不同位置的总变形量,前三阶所对应最大变形量分别为203.56 mm,183.75 mm,216.16 mm。因此,图中最大变形区域为振动敏感区域。表1为模态分析所得PCB前三阶模态固有频率。

图4 分机壳体Fig.4 Extension housing

图5 一阶模态振型Fig.5 The first-order vibration mode
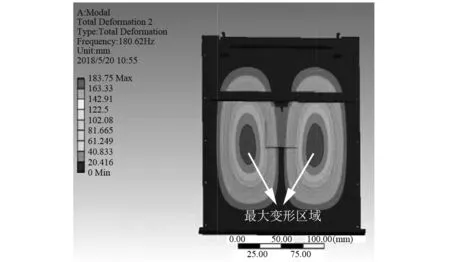
图6 二阶模态振型Fig.6 The second-order vibration mode

图7 三阶模态振型Fig.7 The third-order vibration mode

表1 PCB前三阶模态频率Tab.1 The first three-order modal frequencies of the PCB
通过有限元模态分析,确立了颗粒阻尼安装的敏感区域,为了更进一步确定阻尼器的安装位置,将通过谐响应深入分析。
1.3 谐响应分析
通过电路板的谐响应分析可以确定颗粒阻尼器的安装位置并能得到PCB的峰值频率。在模态分析的基础上,对PCB采用模态叠加法进行谐响应分析并求解。求解频段为模态分析所得电路板固有频率的最小值与最大值,响应的输出为加速度频率曲线。求解条件为:针对PCB的芯片沿X轴方向施加6 mm/s2的加速度(见图8),求得节点位置的加速度频率曲线(见图9)。

图8 节点位置Fig.8 Node position

图9 加速度频率曲线Fig.9 Acceleration frequency curve
根据以上谐响应分析结果,由加速度频率曲线可知,电路板上的加速度幅值在频率为118 Hz,181 Hz,280 Hz时振幅出现了峰值,分别为14.52 m/s2,24.86 m/s2,9.13 m/s2且在频率为181 Hz时,峰值为最大值。因此,针对PCB的减幅,将重点关注二阶模态固有频率。通过谐响应分析,确定阻尼器的安装区域为二阶模态振型处。
1.4 颗粒阻尼器的设计
颗粒阻尼器是高度的非线型阻尼器,这种阻尼机制随着颗粒的材料、尺寸、填充率等参数的变化而变化[18-20],基于多变参数前提下,阻尼器的设计尤为重要。
阻尼器的尺寸越大,能够填充的颗粒越多,一般阻尼效应也有一定程度的提高,但是PCB的使用面积也会大大减少。因此,在阻尼器形状的选择上,考虑有效空间的最大利用率,通过在振动的模态点位置合理的设计阻尼器,并进行阻尼器的优化,力争做到用最小的质量获得最优的质量比,从而得到最佳的使用面积。
基于PCB的布局,本文采用正方形阻尼器,其外部尺寸为30×30×8(mm),阻尼器材质为ZAlZn6Mg铝合金,采用厚度为1.0 mm的铝板进行封闭,阻尼器与PCB板之间采用M2十字沉头螺栓进行连接。为保证阻尼器与PCB之间的固定相连,螺栓底部螺纹可以打上螺纹胶,防止长期使用过程中螺钉的脱落造成阻尼器松动,三维结构如图10所示。

图10 阻尼器设计Fig.10 Damper design
2 基于PCB颗粒阻尼器模型的建立
颗粒间通过接触碰撞由此产生法向力与摩擦的切向力,因此,基于计算的精度及速度,本文在不考虑颗粒间接触力的叠加上,引入了弹性力与阻尼力,并将法向简化为线性接触模型,切向简化为库伦摩擦力模型。在PCB上装有颗粒阻尼器,给出了颗粒间以及颗粒与阻尼壁板间的接触模型,如图11所示,其中:kn为颗粒的法向刚度;cn为颗粒的法向阻尼;kt为颗粒切向刚度;ct为颗粒切向阻尼;μ为耦合器,用来确定颗粒的配对关系。
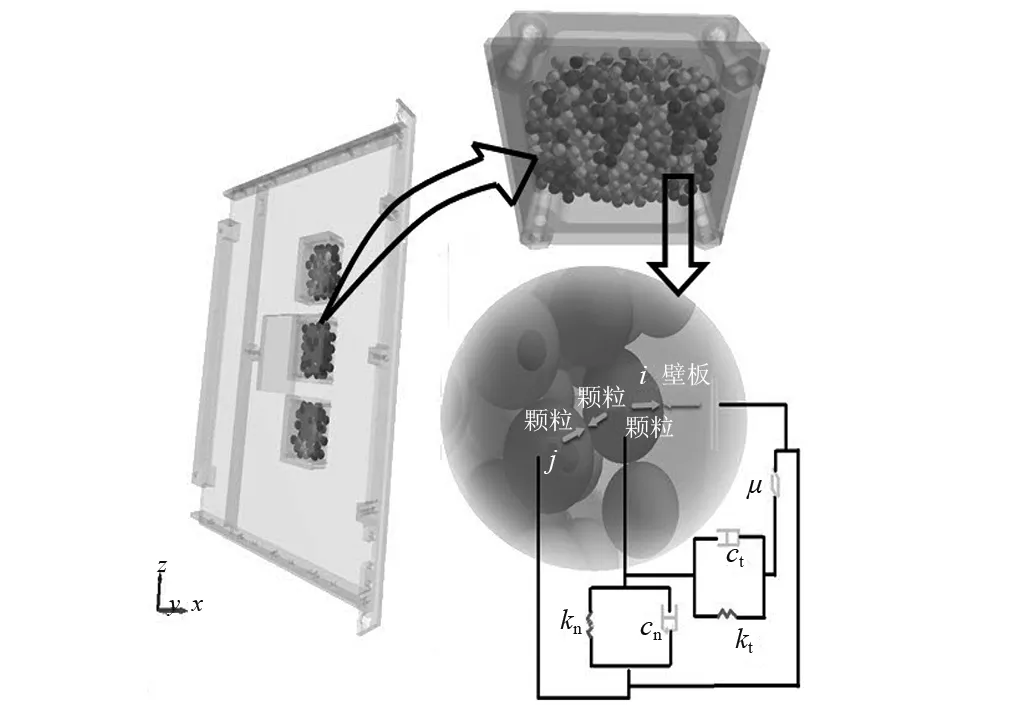
图11 颗粒的离散元模型Fig.11 Particle discrete element model
PCB在运动过程中,阻尼器中颗粒在某一时刻的运动方程为
(4)
(5)
式中:Fn与Ft为颗粒i,j之间法向接触力与切向接触力;pi为颗粒位移向量;g为重力加速度;mi为颗粒的质量;Ii为颗粒惯性矩;φi为颗粒角位移矢量;T为切向产生的扭矩;si为某时刻与颗粒i接触颗粒数量。法向合力可以表示为
Fn=Fkn+Fcn=-knDn-cnVn
(6)
式中:Dn为颗粒间法向变形量;Vn为粒子间的法向相对速度,可由Hertz接触理论得出具体值。
用P-P表示颗粒与颗粒,用P-D表示颗粒与阻尼器壁板,则法向弹性系数kn可表示为[21]
(7)
(8)
式中:E为接触单元的弹性模量;V为泊松比;R为颗粒半径;m为接触单元等效质量。
切向合力可以表示为
Ft=Fkt+Fct=-ktDt-ctVt
(9)
式中:Dt为颗粒间切向变形量;Vt为粒子间的切向相对速度。根据Hertz接触模型,kt与ct可推导为
kt=rkn
(10)
r为比例系数
(11)
(12)
式中:m为接触单元等效质量;G为接触单元的切变模量。
颗粒阻尼的耗能包括碰撞耗能和摩擦耗能。当任意两个颗粒i,j发生碰撞接触时,碰撞耗能表示为
(13)
式中:e为颗粒的恢复系数;Δv为两颗粒碰撞前的相对速度。
摩擦力做功决定了摩擦耗能的大小,表示为
ΔEn=μFnΔS
(14)
式中:μ为两颗粒之间的摩擦因素;ΔS为两颗粒切向相对位移。
颗粒系统的总体能耗可表示为
E=ΣΔEm+ΣΔEn
(15)
3 PCB阻尼器参数的确定
3.1 颗粒粒径的选择
为了使PCB上模态敏感点处的阻尼器具有更高效的减振能力,针对阻尼器的粒径进行探索优化,图12为仿真模型。在阻尼器填充空间有限的情况下,优选比重较大的颗粒,因此本文以钨合金为材料,泊松比为0.28,密度为1.935×104kg/m3,弹性模量为3.24×1011Pa。
3.1.1 颗粒的粗优化
颗粒过小,则颗粒越接近于流体的形态,失去了固态的特性,如果颗粒过大,颗粒间隙过大,碰撞次数较少。本文粗选颗粒粒径为1 mm,1.5 mm,2 mm,2.5 mm,3 mm填充率85%为例。在离散元软件中导入模型,添加颗粒的生成界面,给予模型为X轴的振动5 mm,频率设置为181 Hz的正弦运动。基于仿真效率与速度,仿真时间设置为1 s。

图12 颗粒模型样图Fig.12 Particle model figure
如图13通过离散元方法分别统计不同颗粒尺寸不同时刻的耗能效果。表2为1 s内颗粒总能量耗散情况。经过粗选的颗粒尺寸,从图表中易得2 mm的钨合金颗粒耗散能量最大。但随着颗粒尺寸的增大能耗有所下降,后文将通过试验进行进一步探究。

图13 不同时刻的耗能图Fig.13 Different time diagram of energy loss

表2 颗粒的总能耗Tab.2 Total energy loss of particles
3.1.2 颗粒的细优化
基于粗选的颗粒尺寸,2 mm颗粒的耗能效果显著。为此,以2 mm尺寸为界,进一步探索细微尺寸的能耗效果。细选粒径为1.8 mm,1.9 mm,2 mm,2.1 mm,2.2 mm,填充率为85%,参数设置不变。如图14通过离散元方法分别统计细微颗粒尺寸的耗能效果,能得到不同时刻的能量耗散情况。表3则为1 s内的颗粒总能量耗散情况。经过细选的颗粒尺寸,从图表中易得1.9 mm的钨颗粒耗散能量最大。因此,细选1.9 mm的钨颗粒具有最佳减振效果。
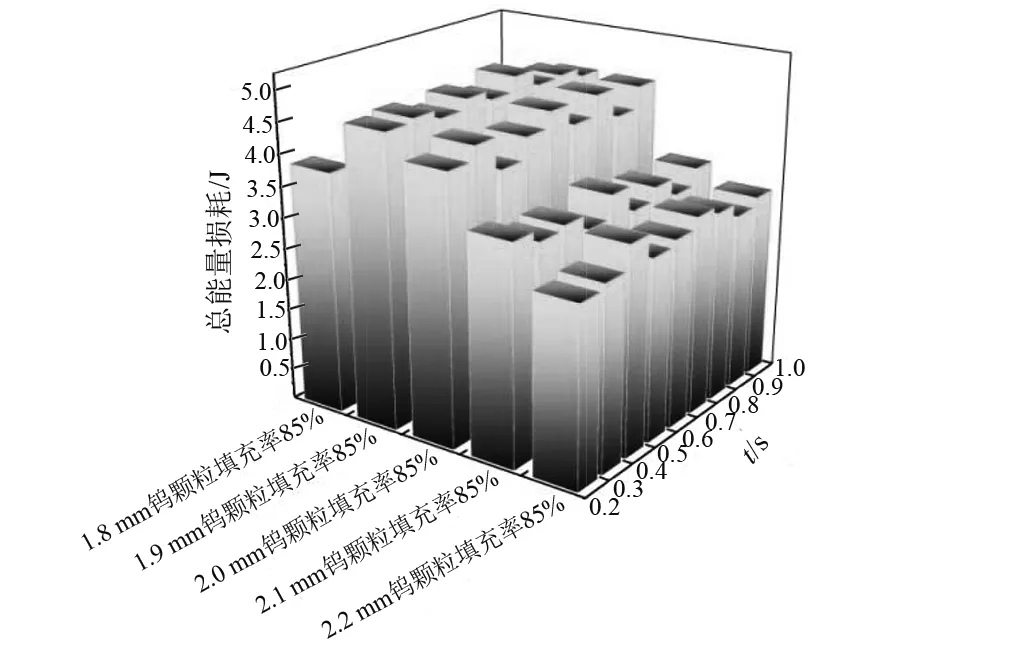
图14 不同时刻颗粒的耗能图Fig.14 Different time diagram of energy loss

表3 颗粒的总能耗Tab.3 Total energy loss of particles
3.2 颗粒填充率的优化
在离散元软件中导入模型,设置相同的参数与运动情况。阻尼颗粒需要保证在有限空间内能够有一定的运动行程,这样才能增大颗粒与颗粒之间摩擦与碰撞的机会,如图15所示,本文以填充率为75%,80%,85%,90%,95%为方案,1.9 mm钨合金材料颗粒为例,进行仿真计算。

图15 填充率模型样图Fig.15 Fill rate model figure
不同深浅的颗粒表示了不同的运动速度,颜色越深,颗粒速度越大。如图16所示,通过离散元方法分别统计不同填充率颗粒阻尼器不同时刻的能量损耗。表4则为不同填充率下颗粒的总能耗。根据能量损失图表易得随着颗粒填充率的不断提高,颗粒阻尼效果越明显,90%填充率的钨合金颗粒耗散能量最大。但是当颗粒填充率到达95%时,耗能情况有显著的下降。
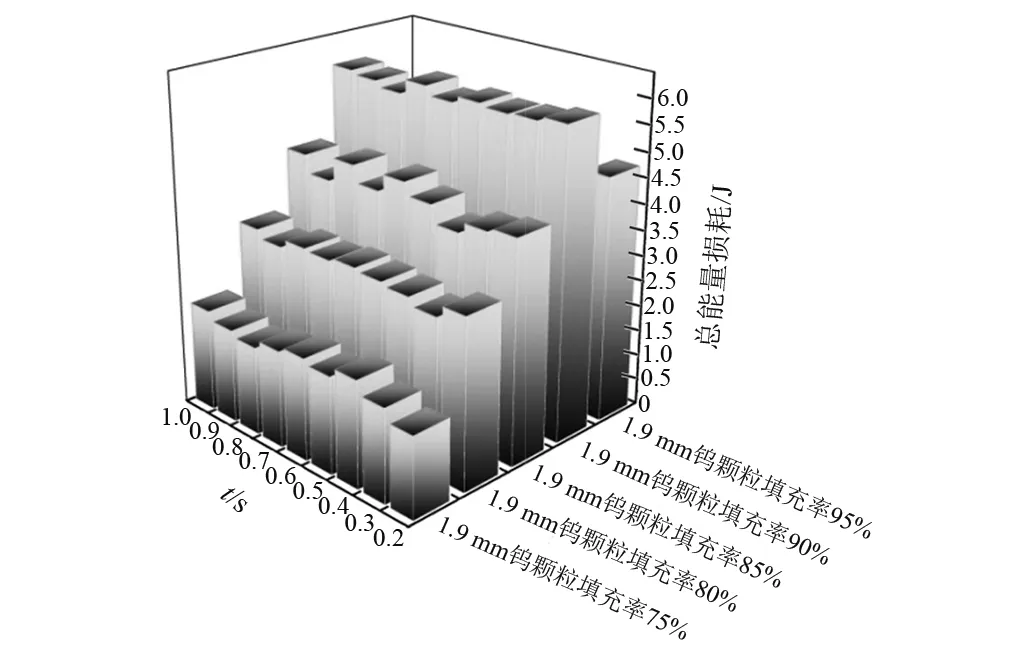
图16 不同时刻耗能图Fig.16 Different time diagram of energy loss

表4 颗粒的总能耗Tab.4 Total energy loss of particles
3.3 颗粒尺寸与填充率的关联
上文对颗粒尺寸的优化和颗粒填充率的优化是分开进行的,为了验证二者之间的关联性,寻求最佳的适配值,做出如下仿真。仿真参数与过程与前文相同,颗粒尺寸以1.5 mm,1.8 mm,1.9 mm,2 mm,2.5 mm,填充率以80%,85%,90%,95%为方案。不同粒径对应不同填充率的耗能情况,如图17所示。
不同的粒径有最佳的填充率,1.5 mm粒径最佳填充率为85%,1.8 mm,1.9 mm,2 mm,2.5 mm最佳填充率为90%。当选择1.9 mm粒径,填充率为90%时,它的总能耗值是最高的。因此,对于本文而言,当颗粒直径为1.9 mm时,其所对应的最佳适配填充率为90%。
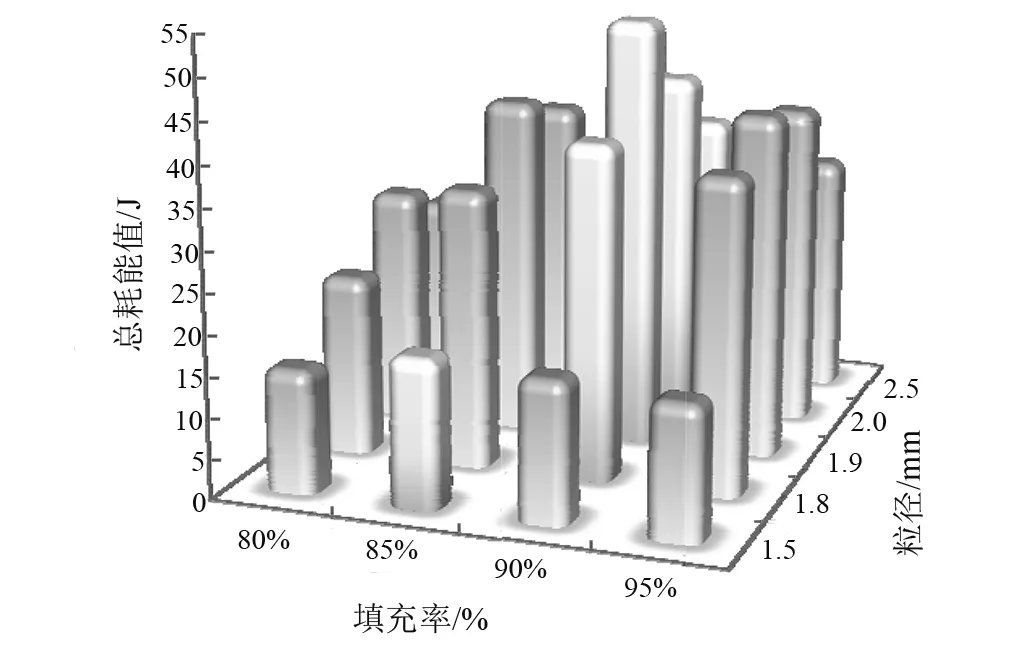
图17 总耗能Fig.17 Total energy loss
3.4 仿真结论
基于钨颗粒的离散元分析,分别从颗粒的尺寸大小、填充率以及二者的关联性进行仿真优化。验证了阻尼器参数在钨颗粒粒径大小为1.9 mm,填充率为90%时能使PCB达到最优化的减振效率,确定最优阻尼的配置设计方案为下一步电路的设计奠定基础。
4 试验验证
针对北京华航无线电测量研究所某PCB,设计制造样机试验用壳体、试验用阻尼器外壳,选择测点,进行颗粒粒径、填充率的试验验证。
PCB结构尺寸为192×179×2(mm),PCB材料为FR-4,重量为226×10-3kg,用加速度传感器实测PCB在正弦振动时的均方根值,规定PCB的整体方位与测点如图18(a)所示。由于PCB上已经布满了现有电路,增加阻尼器不能对电路造成破环,为此,增加阻尼器位置为无电子线路的空白PCB部分。
PCB的外层壳体如图18(b)所示,图上所示的三个方位与PCB的方位相匹配,从而实现完美的对接。阻尼器采用厚度为1.0 mm的铝板进行封闭,重量达到15×10-3kg(包括紧固件),加工实物图如图19所示。在振动台上(见图20),长箭头的表示振动台的主振方向,平行于长箭头的短箭头为PCB的X方向,图示为PCB主振X的方向。
基于动力学分析,对PCB的减振,将重点关注二阶模态固有频率,为了达到消减峰值的目的,阻尼器将安装于二阶模态振型处。

图18 电路板与分机壳体Fig.18 Circuit board and extension housing

图19 阻尼器实物图Fig.19 Damper physical figure

图20 主振X方向Fig.20 The main vibration direction of X
4.1 颗粒粒径的验证
PCB通过夹具固定在振动台上,实测样机在正弦振动下的响应,设置参数为沿主振X方向振动5 mm,设置频率为181 Hz。探索不同颗粒直径对减振效果的影响,以1 mm,1.5 mm,1.9 mm,2.5 mm,3 mm颗粒尺寸,填充率为85%为例,采用图21的布置方案,颗粒尺寸如图22所示,所得加速度均方根值如表5所示。

图21 排布方案Fig.21 Arrangement plan

图22 颗粒尺寸Fig.22 Particle size
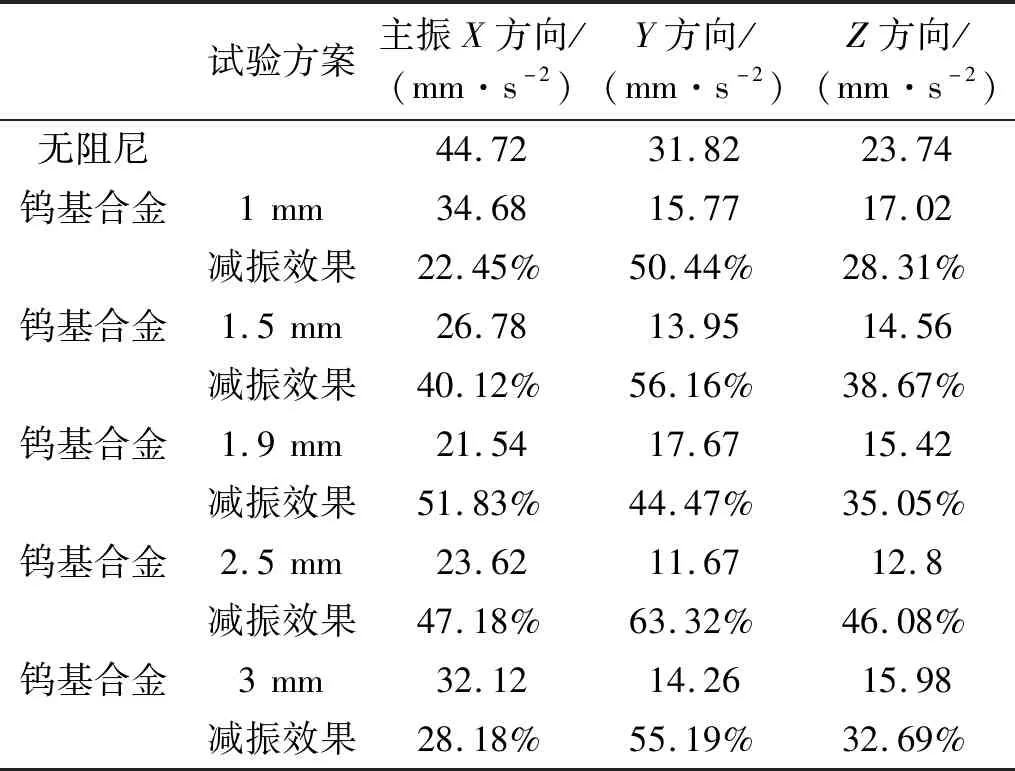
表5 测点加速度均方根值Tab.5 Measured point acceleration RMS
由表5的数据可明显得出,在颗粒的主振方向上,直径为1.9 mm的钨颗粒减振效果优于其他粒径的钨颗粒。减振效果在主振方向上可以达到50%以上,将试验结果与仿真结论进行对比。如图23所示,两条曲线具有高度的相似性,均证明了对于本文的PCB,1.9 mm尺寸的钨颗粒具有较好的减振效果。

图23 试验与仿真对比图Fig.23 Comparison of test and simulation
4.2 颗粒填充率的验证
PCB通过夹具固定在振动台上,实测样机在正弦振动下的响应。探索不同填充率对减振效果的影响,以1.9 mm钨颗粒,75%,80%,85%,90%,95%填充率为例,采用图21的布置方案,所测得加速度均方根值如表6所示。

表6 测点加速度均方根值Tab.6 Measured point acceleration RMS
从颗粒的填充率上来看,90%填充率的钨颗粒减振效果优于其他填充率的钨颗粒。试验中减振效果在主振方向上可以达到50%以上,效果十分明显。将试验结果与仿真结论进行对比,如图24均证明了对于本文的PCB,90%钨颗粒填充率具有较好的减振效果。

图24 试验与仿真对比图Fig.24 Comparison of test and simulation
4.3 阻尼器安装位置的验证
基于有限元动力学分析,在二阶模态固有频率为181 Hz时,振动峰值达到最大点。对于本文的PCB,基于原有电路的设计,在接线与元器件排布位置的基础上,只留下图25中非敏感位置。
针对电路板进行扫频分析,扫频范围为0~330 Hz,通过频谱图验证PCB上敏感区域与非敏感区域加阻尼器的减振效果。如图26所示,图26(a)为非敏感区域电路板安装阻尼器的方案,图26(b)为敏感区域电路板安装阻尼器的方案。
对比试验结果,通过频域曲线进行分析,如图27所示,在非敏感区域安装颗粒阻尼器后,总有效值从40.75 mm/s2降到了39.33 mm/s2,没有明显的减振效果。在敏感区域加上阻尼器后,总有效值从40.75 mm/s2降到了20.50 mm/s2,降幅在主振方向上可以达到50%。二阶频率的峰值从27.35 mm/s2降到了15.80 mm/s2,达到很好的降峰效果,整体减振效果十分显著。

图25 电路板的非敏感区域Fig.25 Non-sensitive area of the circuit board

图26 阻尼器安装位置Fig.26 Damper installation position

图27 频谱图Fig.27 Spectrogram
5 结 论
(1)针对目前PCB结构及振动条件,在阻尼器形状的选择上,需考虑有效空间的最大利用率,并通过敏感点的位置合理的设计阻尼器。在颗粒阻尼参数的选择上,采用钨基合金颗粒,理论直径为1.9 mm,填充率为90%时,电路板达到最优化的减振效果。
(2)基于动力学特性分析寻求模态敏感区域,通过阻尼器安装位置的选择,验证在敏感区域安装阻尼器能使PCB在主振方向上达到50%减振效率。
(3)本文提出PCB的动力学分析与电路联合设计方法,改善了PCB的抗振特性。基于布线合理性、布通率与电气性,调整元器件位置与接线布置使得在电路板模态敏感点区域留出余裕。在非敏感区域设计电路,在敏感区域安装颗粒阻尼器。针对颗粒阻尼器模型设计与构建,完成整个电路体系的设计,大大提升了导弹电子设备的稳定性。

