睡眠分期的双谱域快慢同步比研究

刘 戈，刘洪运，石金龙，王国静，胡敏露，王卫东*

（1.解放军总医院研究生院，北京 100853；2.解放军总医院第一医学中心医学工程保障中心，北京100853；3.解放军总医院第一医学中心医疗器械研发与临床评价中心，北京 100853）

0 引言

睡眠是一项非常重要的生命过程，睡眠分期的研究结果是评估睡眠质量的重要标准。2007年，美国睡眠医学学会（American Academy of Sleep Medicine，AASM）将睡眠时相划分为五期，包括清醒期（wakefulness，W）、非快速眼动期Ⅰ期（non-rapid eye movementⅠ，N1）、非快速眼动期Ⅱ期（non-rapid eye movementⅡ，N2）、非快速眼动期Ⅲ期（non-rapid eye movementⅢ，N3）和快速眼动期（rapid eye movement，REM）。目前AASM标准逐渐被广泛应用。

脑电（electroencephalogram，EEG）是睡眠过程中最显著和最直观的信号，大量研究证明，EEG是研究睡眠分期最重要的生理信号，其用于睡眠分期的效果大大优于其他生理信号[1-4]。EEG在不同的睡眠时相中表现出不同的特征节律波，AASM标准下不同睡眠时相的特征节律波及其频率与幅值范围[5]见表1。不同睡眠时相的EEG节律波不同是使用EEG信号作睡眠分期的基础。

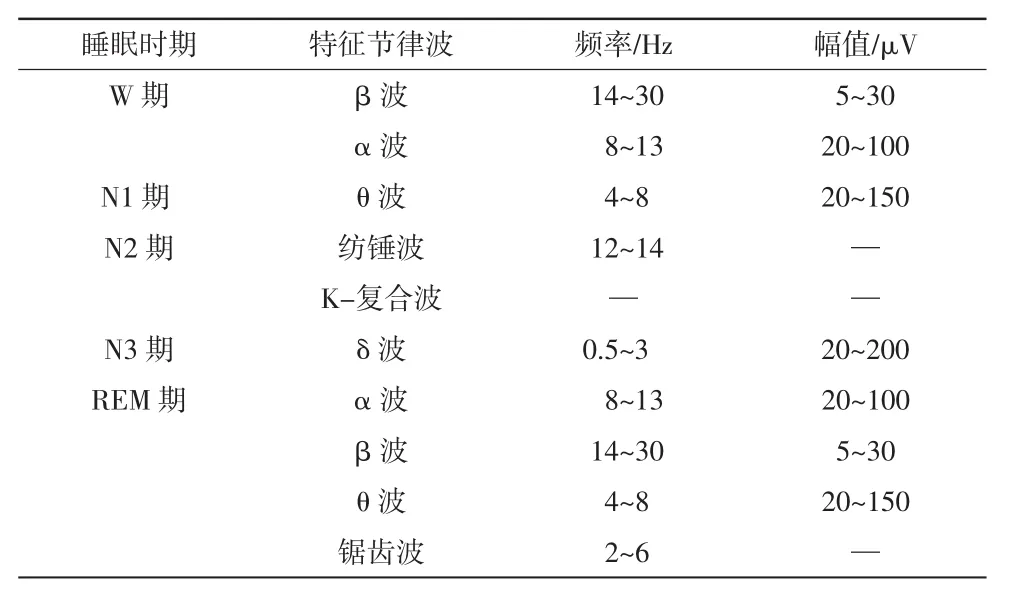
表1 各睡眠时相特征波分布

传统的睡眠EEG的分析方法主要有时域、频域、非线性分析方法。时域分析是出现最早且最直观的一种分析方法，频域分析仅能发掘信号的频域特征，这2种分析方法对于EEG这种非平稳、非线性信号而言存在一定的局限性。非线性分析方法，如样本熵、模糊熵、功率谱熵等适用于EEG信号[6-8]，但该类方法忽略了非高斯过程的某些有用信息，如相位信息。双谱分析可以发现睡眠EEG的相位耦合信息，目前国内外将双谱特征用于睡眠分期的研究不多。Acharya等[9]使用EEG信号双谱特征进行睡眠分期，准确率可达88.7%。王月荣[10]发现双谱分析的最大幅值可以有效区分大鼠睡眠不同阶段。本研究拟在双谱域定义一种新的用于睡眠分期的特征。

1 双谱与快慢同步比的定义

高阶统计量[11]是指阶数大于二阶的统计量，主要有高阶矩、高阶累积量和高阶累积量谱（以下简称“高阶谱”）等内容。在信号处理领域，人们习惯假设信号或者噪声服从高斯分布，然而真实信号大都是非高斯的，因此传统的分析方法丢失了非高斯过程的某些有用信息，高阶谱分析则可以提供十分丰富的信息，如：可展现EEG信号的二次相位耦合信息。在非高斯信号中，一些非线性过程的2个频率成分会因两者的互相作用在它们的和频率或差频率处产生新的能量，这种非线性相互作用被称为二次相位耦合作用。在EEG、耳声发射、旋转机械产生的信号中均有二次相位耦合现象发生。高阶谱另一方面的优势为抑制高斯噪声。由于高斯过程三阶及以上累积量均为0，而K阶谱是K阶累积量的K-1维博里叶变换，所以高阶谱可以有效抑制信号的背景高斯噪声。

双谱（即三阶谱）是最常用、最简单的高阶谱。双谱是三阶累积量的二维傅里叶变换，其公式如下：

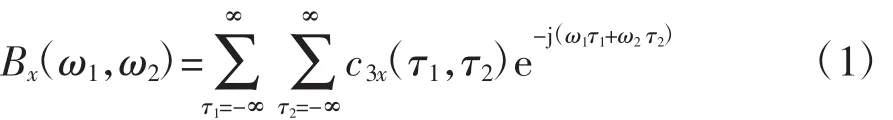
其中，双谱值B反映的是（ω1，ω2）处的幅值相位耦合能量，τ1、τ2为三阶累积量c3x的时延，ω=2πf（f为归一化频率）。

我们所熟知的功率谱即为二阶谱，它是二阶累积量的一维傅里叶变换，其抑制了所有的相位关系，仅能反映每个频率处的幅值信息。而双谱为二维复函数，它具有幅度和相位信息，因此双谱分析不仅能够检测信号的幅度信息，还能检测信号的相位信息，并量化幅值相位耦合能量。下面举一个例子，定义2个三角函数：其中，k为自变量；λ1、λ2、λ3为三角函数的角频率，且λ3=λ1+λ2；φ1、φ2、φ3为独立随机变量，范围为[0，2π]。XⅠ（k）中φ3是一个独立的相位随机变量，因此λ3是一个独立的谐波分量。而XⅡ（k）中最后一个分量的相位为φ1+φ2，因此λ3是相位耦合的结果。

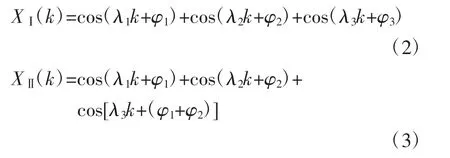
2个函数的功率谱和双谱如图1、2所示。

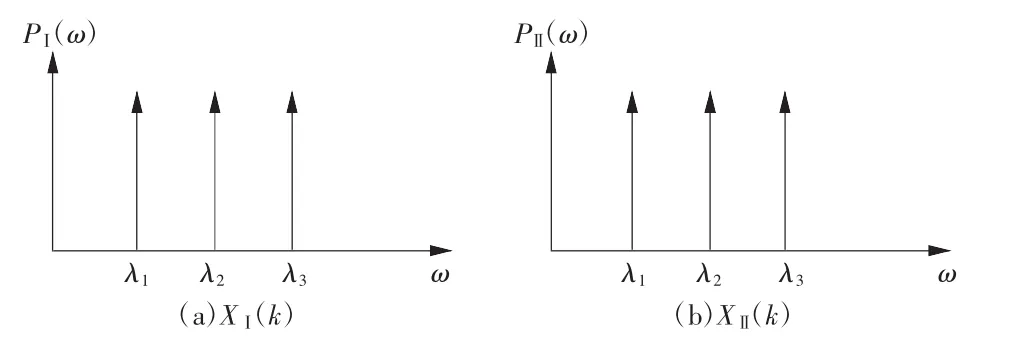
图 1 XⅠ（k）、XⅡ（k）功率谱

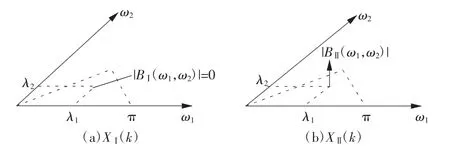
图 2 XⅠ（k）、XⅡ（k）双谱

由图1、2可以看出，XΙ（k）和XⅡ（k）的功率谱完全一样，而在双谱中，XΙ（k）的双谱为0，XⅡ（k）的双谱在（λ1，λ2）处表现为一个脉冲，即存在二次相位耦合。上述分析说明双谱能够发现功率谱中发现不了的相位耦合信息。

EEG信号的双谱分析方法也类似于功率谱估计方法，包括非参数化方法和参数化方法。图3为使用非参数化方法中的平均周期图法输入采样频率为100 Hz的30 s不同睡眠时相的EEG信号得到的双谱图。可以发现，不同睡眠时相的EEG信号表现出来的幅值相位耦合信息有明显差别。本文将在双谱图的基础上进一步研究用于睡眠分期的定量特征。

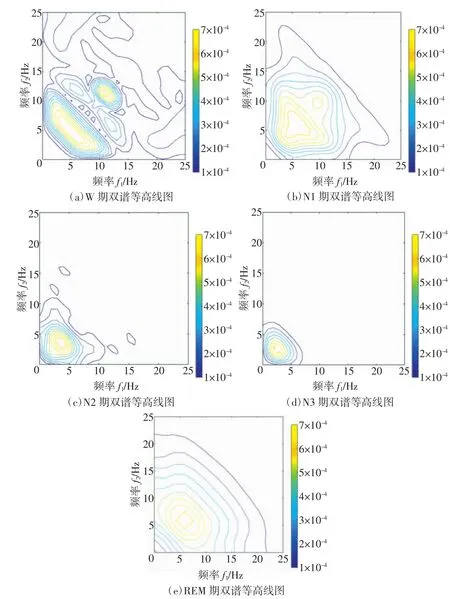
图3 睡眠五期双谱图

快慢同步比[12]是应用于麻醉深度检测的EEG双频指数（bispectral index，BIS）值的子参数，它能够反映相位耦合的特征。BIS于1996年被美国食品药品监督管理局（Food and Drug Administration，FDA）批准用于麻醉镇静深度监测，是目前临床上应用最广泛的麻醉镇静深度评价指标[13]。本研究之所以拟将BIS子参数快慢同步比应用于睡眠分期，是因为全身麻醉和睡眠一样也是由浅入深，麻醉过程的意识逐渐模糊到失去意识可类比于睡眠状态的由浅入深。快慢同步比即为频率较快的耦合信号能量与频率较慢的耦合信号能量的比值。在BIS指数中，快慢同步比的定义[14-15]为

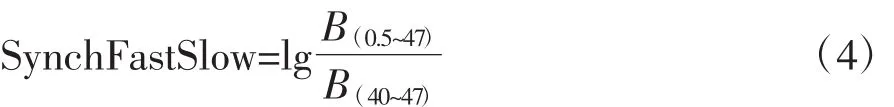
其中，B（0.5~47）代表整个 EEG 频域 0.5～47 Hz的双谱值之和，B（40~47）代表高频区域 40～47 Hz的双谱值之和。两者之比取对数作为反映双谱分析中相位耦合信息的指标——快慢同步比。

2 基于快慢同步比的睡眠分期

2.1 实验数据

本文使用Physionet生理信息库中sleep-EDF数据库的11名受试者整夜睡眠实测数据，包括6名健康志愿者的睡眠数据、5名有轻微失眠志愿者的睡眠数据。使用Fpz-Cz和Pz-Oz导联EEG信号，受试者包括3名男性和8名女性，年龄范围21～65岁。测试过程中未使用任何药物干扰，采样频率均为100 Hz。数据库中每30 s的EEG信号的睡眠分期结果已由专家人工进行了标注（以R&K睡眠分期标准标记）。定义30 s EEG数据为一个样本。个别受试者会将整夜睡眠数据中前后清醒期数据舍弃不用。11名受试者睡眠样本分布情况见表2。

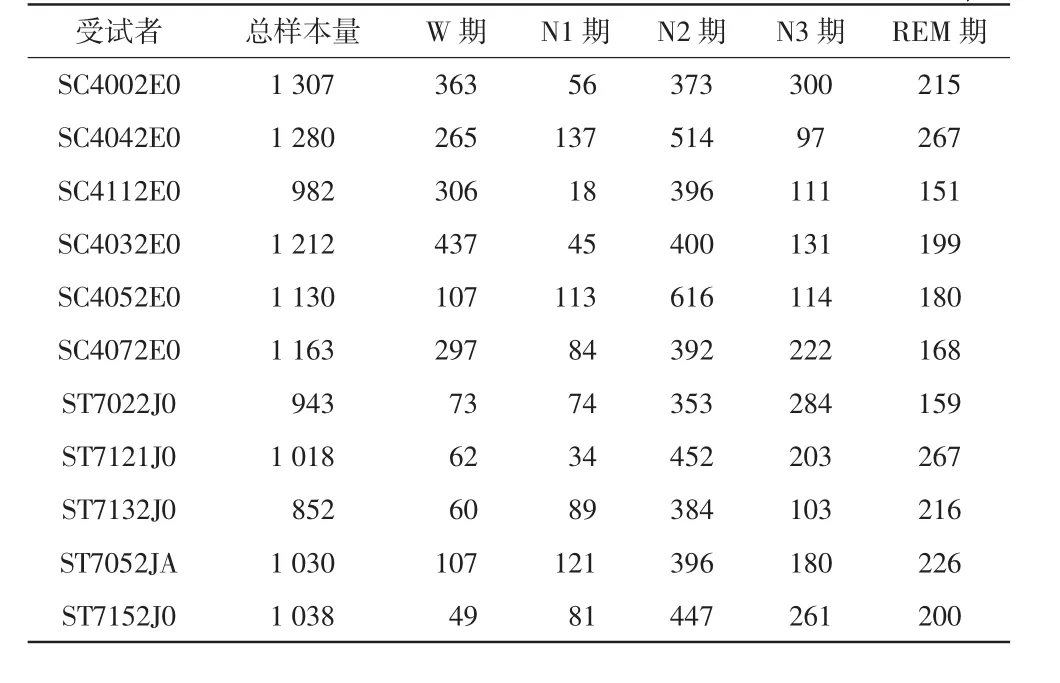
表2 11名受试者睡眠样本分布个

2.2 实验方法

2.2.1 数据预处理

EEG的有用信号集中在0.5～47 Hz频带范围，因此直接选用0.5～47 Hz的FIR（finite impulse response）带通滤波器对原始睡眠脑电数据作滤波处理，为下一步提取脑电信号的有效信息奠定基础。

2.2.2 统计学方法

使用SPSS Statistics 24软件进行统计学分析，首先对睡眠五期各组间快慢同步比进行正态性检验和方差齐性检验，在满足正态分布的前提下，若方差齐则使用SNK组间检验，方差不齐使用Dunnett T3组间检验。不满足正态分布的情况下，使用非参数秩和检验。显著性水平均为0.05。

2.2.3 选取最优快慢同步比定义

将公式（4）定义的快慢同步比直接用于睡眠分期时效果很差，根本不能够区分睡眠各时相。因此，结合图3中各睡眠时相双谱值集中的频带范围，以及引言部分不同睡眠时相的特征波频带范围，拟在公式（4）定义的原快慢同步比的基础上进行频带范围的更改，作为睡眠分期的特征值。用于睡眠分期的双谱域的快慢同步比定义如下：a取有用睡眠EEG信号的频率上限，本研究中取30、40两个值；参考图3中各睡眠时相双谱值频带变化，b取 θ波、α 波的上限值（8、13 Hz）以及中间值（10 Hz）。共计得到6种快慢同步比定义：

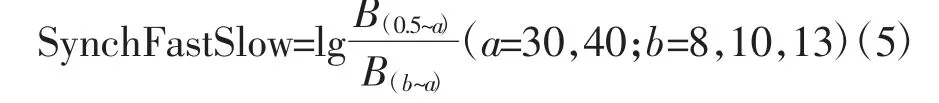
任意选取某2名受试者的EEG样本数据，求出上述6种定义下的快慢同步比，分别进行统计学分析，选出对睡眠五期分期效果最优的定义。

使用sleep-EDF数据库中的SC4002E0受试者整夜共10多个小时的Fpz-Cz导联睡眠数据和ST7121J0受试者共8个多小时的Fpz-Cz导联睡眠数据对不同定义下的快慢同步比进行分析。各组数据均满足正态性检验，但方差不齐，使用Dunnett T3组间检验。图4、表3及图5、表4为不同定义下的2名受试者睡眠各期快慢同步比均值及组间统计学分析结果。

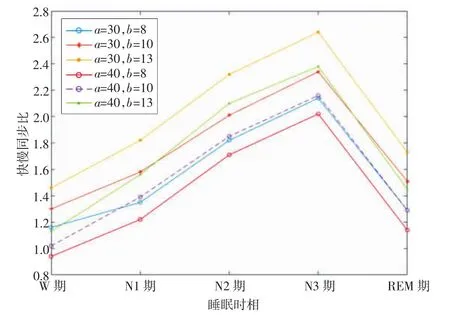
图4 SC4002E0受试者不同定义下的睡眠各期快慢同步比平均值

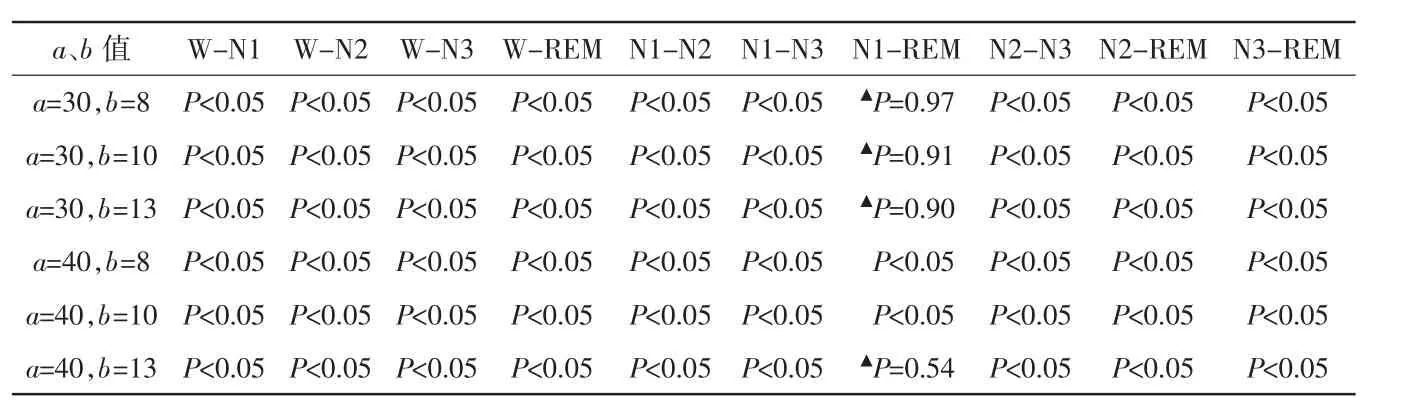
表3 SC4002E0受试者不同定义下的快慢同步比组间统计学分析结果

由图4、表3及图5、表4可以看出，上述6种定义下的快慢同步比对睡眠时相划分均有效，只是各睡眠时相间的差异性略有不同，且不同受试者之间有一定的差异。对于受试者SC4002E0，当a=40，b=8和a=40，b=10时分期效果最好，睡眠五期各期之间均有显著统计学差异。其他定义下的非快速眼动期N1期与REM期没有显著性差异。而对于受试者ST7121J0，当a=40，b=10和a=30，b=13时效果最好。因此，使用以上2名受试者共2 325个睡眠样本数据进行统计学分析后，本文取a=40，b=10定义快慢同步比。即

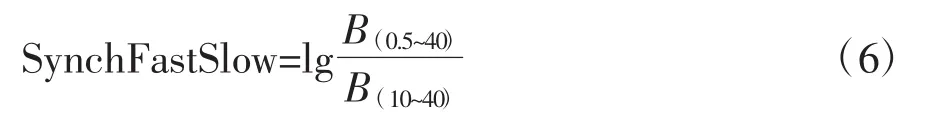
然后将快慢同步比应用于更多测试者，并使用统计学分析方法研究其睡眠分期效果。

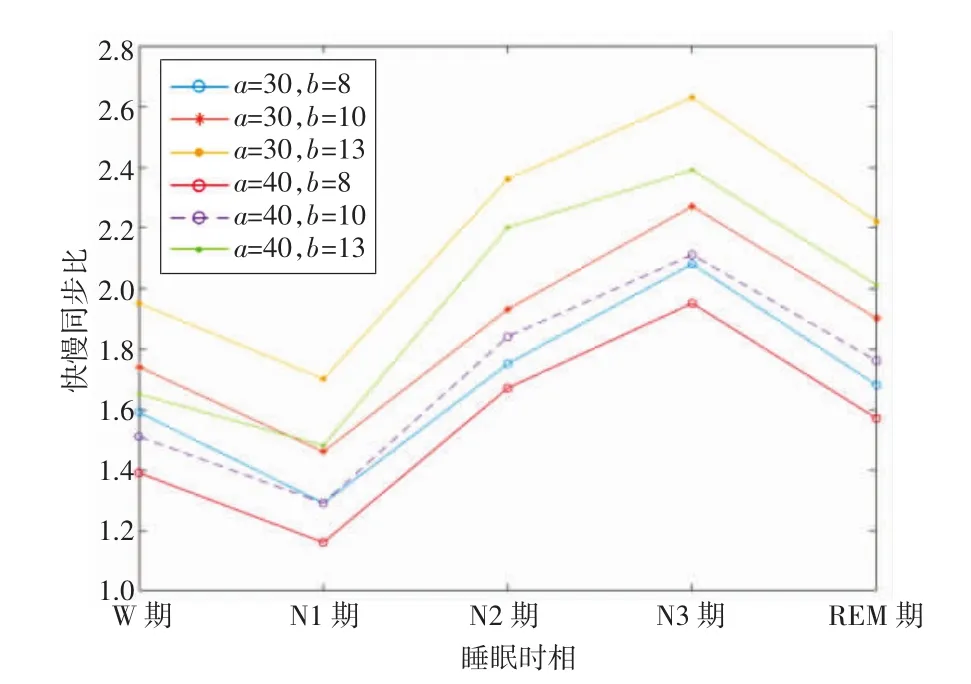
图5 ST7121J0受试者不同定义下的睡眠各期快慢同步比平均值

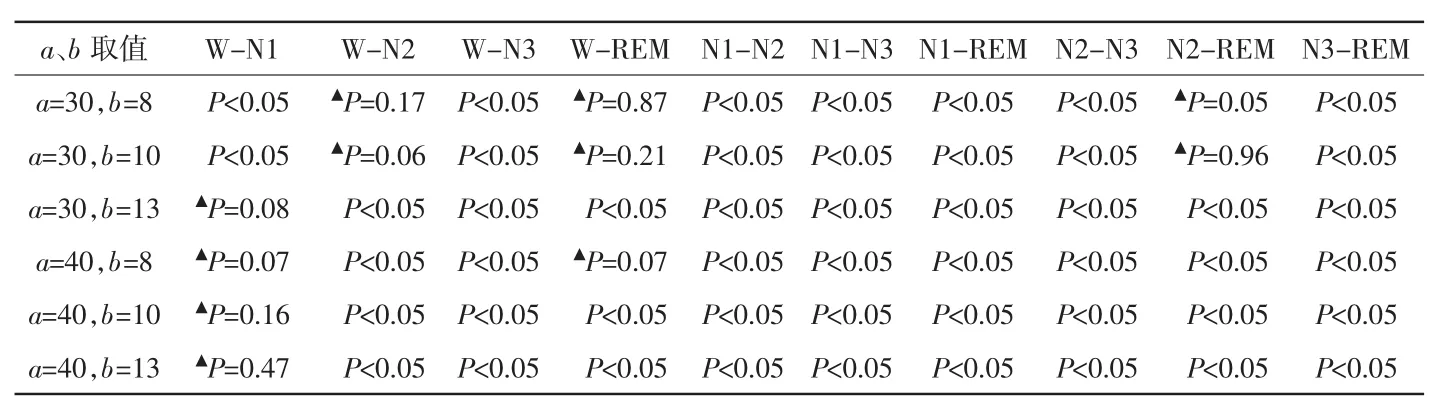
表4 ST7121J0受试者不同定义下的快慢同步比组间统计学分析结果

2.3 结果分析

基于公式（6）的定义，输入其他9名受试者不同睡眠时相的样本数据，得到11名受试者Fpz-Cz导联下的睡眠各期快慢同步比均值，见表5。

另外，使用11名受试者Pz-Oz导联EEG数据作睡眠各期快慢同步比分析，得到睡眠各期快慢同步比均值，见表6。

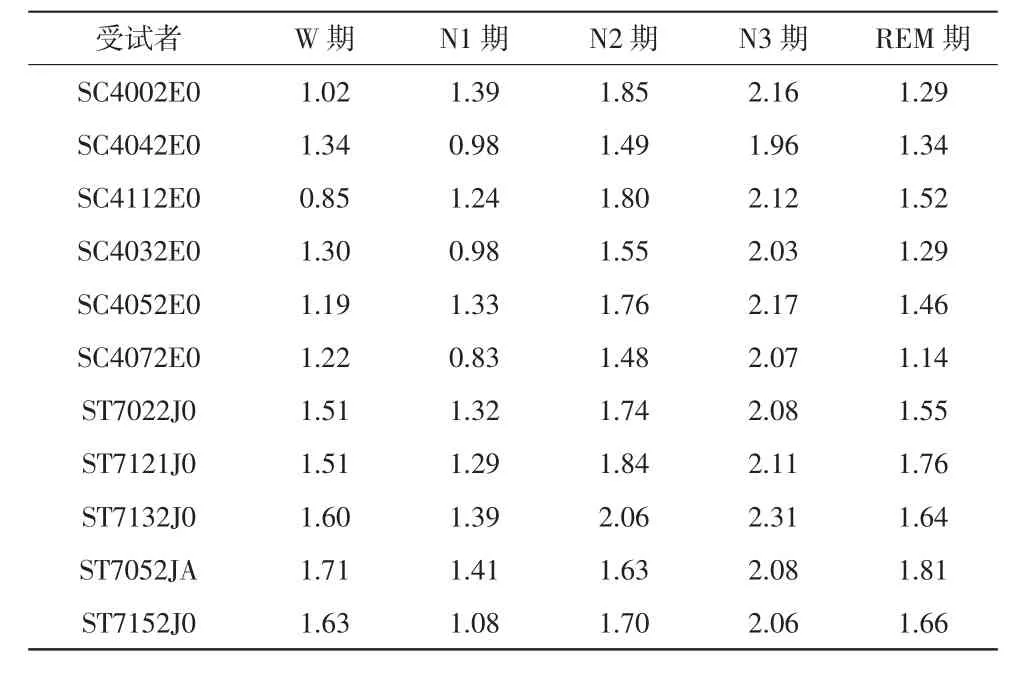
表5 11名受试者睡眠各期快慢同步比平均值（Fpz-Cz）

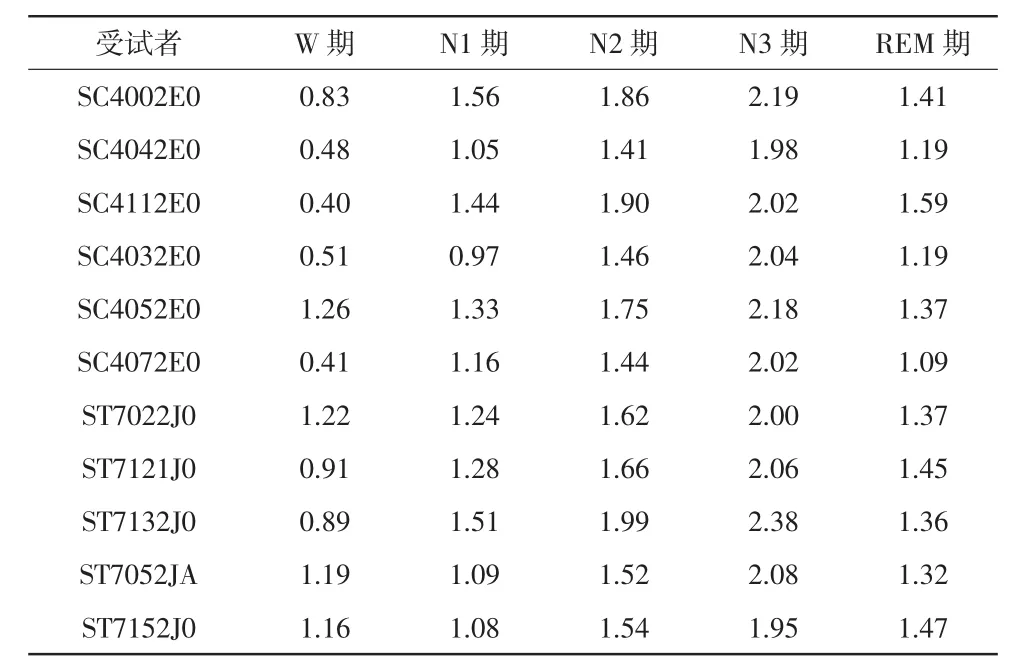
表6 11名受试者睡眠各期快慢同步比平均值（Pz-Oz）

对11名受试者睡眠各期的快慢同步比值进行统计学分析，各组数据均满足正态性检验，作方差齐性检验，由于各组间P＜0.001，方差不齐，使用Dunnett T3组间检验。统计学结果见表7。

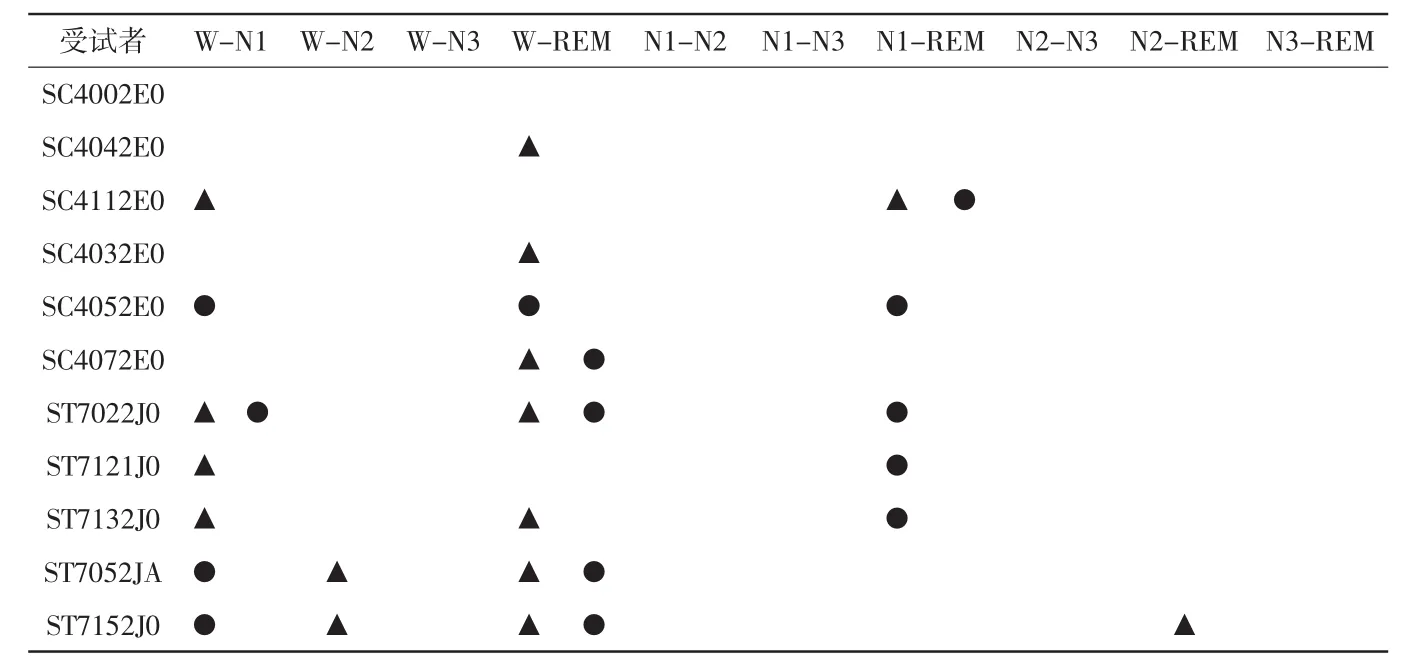
表7 11名受试者睡眠各期快慢同步比组间统计学分析结果

从表5、6可以得出结论，整体而言2个导联睡眠各期的快慢同步比规律性一致。随着睡眠的加深，快慢同步比逐渐增大，在快速眼动期又有所减小。说明随着睡眠的加深，EEG信号相位耦合能量逐渐由高频向低频迁移，到快速眼动期再向高频迁移。本文定义的快慢同步比反映了睡眠过程中幅值相位耦合关系的变化。由表7可知，11名受试者睡眠五期各组间快慢同步比大多有显著性差异。但不同受试者由于年龄、外界刺激、身体状态等不同，睡眠五期快慢同步比的组间差异有所不同，相同受试者2个导联的组间差异也有所不同。对于Fpz-Cz导联而言，效果最好的是受试者SC4002E0和SC4052E0，其各组间快慢同步比均有显著统计学差异。对于Pz-Oz导联而言，效果最好的是受试者SC4002E0、SC4042E0和SC4032E0，各组间均有显著统计学差异。将快慢同步比应用于2个EEG导联，表明快慢同步比在不同导联EEG数据中作睡眠分期的稳定性。

综上可得出结论：本研究定义的双谱域快慢同步比可以作为睡眠分期的一个有效特征，且具有普遍性。

3 结论与讨论

本文研究睡眠EEG的双谱特性，在双谱域定义快慢同步比作睡眠分期研究。将文章定义的快慢同步比应用于11名受试者睡眠EEG数据，发现其对每名受试者睡眠分期有效，2种EEG导联下睡眠五期各期快慢同步比大多有显著统计学差异，也说明快慢同步比这一特征对睡眠分期具有有效性和普遍性。因此，可以将本文定义的双谱域快慢同步比应用于睡眠自动分期。快慢同步比定量分析了不同睡眠时相的EEG幅值相位耦合信息，为睡眠自动分期提供了更多思路。

EEG双谱分析除了可以用于睡眠分期外，还可用在很多方面，如：麻醉深度的检测、癫痫的预测、注意力程度的分析等。黄力宇团队[16-17]发现，癫痫发病时EEG的双相关系数值比发病前和发病结束后的系数值要高得多。将双相关系数和加权双谱中心作为人工神经网络输入时可提前12～24 s预报癫痫的发作。杜英举[18]将双谱应用于注意力程度分析也取得了较好的结果。可以说双谱分析作为最简单的高阶谱分析，对分析典型的非线性信号有着得天独厚的优势。另外，双谱分析在心电、机械电子学也有广泛的应用[19-20]。

本研究不足之处在于，选择快慢同步比最优定义时仅对2名受试者Fpz-Cz导联EEG数据的快慢同步比作了组间统计学分析，可以说仅仅是选择了一个相对最优的定义。但观察每种定义下的快慢同步比对睡眠分期均有效，且每种定义下睡眠各期的数据趋势是一致的，只是各睡眠时相间的差异性略有不同，也证明了将快慢同步比用作睡眠分期是正确且有理论依据的。另外，本文仅研究了高阶谱领域中最简单的双谱（三阶谱），如需分析3组频带甚至更多频带间的相位耦合信息，可以对四阶及以上的高阶谱作研究并对睡眠各期的差异性作定量分析。