基于Python和梯度下降算法的物理实验数据一元线性拟合方法

关毅铬

(华南师范大学物理与电信工程学院 广东 广州 510006)

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析.梯度下降法是一种最优化算法，常用于机器学习和人工智能中用来递归性地逼近最小偏差模型，对数据量大，关系复杂，很难得到解析解的函数关系来说十分有效[1].它是迭代法的一种,可以用于求解最小二乘法问题.所以我们也可以用梯度下降法来处理呈线性关系的实验数据.

1 梯度下降法的介绍

1.1 梯度下降法

一元线性回归其实就是去找到一条直线，这条直线能以最小的误差来拟合数据.

如图1所示，横坐标表示x，纵坐标表示y.一元线性回归要找的就是图中的这条直线，用y=b+mx表示.但是，所有的点都在这条拟合直线上肯定不现实，所以这些点要尽量靠近这条直线.即去找每个点和直线的距离|yie=b+mxi|最小的那条线.为了简单起见，将绝对值转化为平方，那么误差可以表示为

这里i表示第i个数据，N表示总的样本个数.把这个损失方程看作是m和b的方程.作为一个m和b的二次方程，那么求损失函数最小值的问题就转变成了求极值问题.我们可以用梯度下降法求解m和b的值以确定拟合直线.

图1 一元线性回归拟合原理

为了更好地理解梯度下降法，这里把损失函数想象成一个碗，而函数的最小值就是碗底，如图2(a)所示.不管位于这个碗的什么位置，只要往下走，也就是往梯度方向走，沿着梯度一点一点滑下去，就能达到这个最低点.梯度就是下面两个式子.

接下来就要定义步长，用来表示每次滑多长，再定义一个迭代值用来表示滑多少次，这样就能一点一点地靠近最小值.定义好这两个值，计算机就可以一边求梯度，一边向下滑，去更新m和b，最后得到损失函数最小时对应的m和b的值.

也可以这样理解梯度下降法.如图2(b)所示，每一个圈代表一个函数梯度，最中心表示函数极值点，每次迭代根据当前位置求得的梯度(用于确定搜索方向以及与步长共同决定前进速度)和步长找到一个新的位置，这样不断迭代最终到达目标函数局部最优点(如果目标函数是凸函数，则到达全局最优点).

实现梯度下降法的主要Python代码如下所示.

def optimizer(starting_b,starting_m,learning_rate,num_iter):

b = starting_b

m = starting_m

for i in range(num_iter):

b,m =compute_gradient(b,m,learning_rate)

return [b,m]

def compute_gradient(b_current,m_current,learning_rate):

b_gradient = 0

m_gradient = 0

N = float(len(data))

b_gradient = -(2/N)*(y-

m_current*x-b_current)

b_gradient = np.sum(b_gradient,axis=0)

m_gradient = -(2/N)*x*(y-

m_current*x-b_current)

m_gradient = np.sum(m_gradient,axis=0)

new_b = b_current - (learning_rate * b_gradient)

new_m = m_current - (learning_rate * m_gradient)

return [new_b,new_m]

1.2 检验拟合结果的指标

求出m和b的具体数值，即找到了拟合的直线.一般数据处理中会用相关系数r检验两变量的相关性，用拟合优度R2检验回归直线的拟合程度.

相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量.相关系数又叫线性相关系数，一般用字母r表示，用来度量两个变量间的线性关系.当r接近于±1时，可以说两个变量相关性比较好.

相关系数公式为[2]

拟合优度是指回归直线对观测值的拟合程度.度量拟合优度的统计量是可决系数R2.R2最大值为1.R2的值越接近1，说明回归直线对观测值的拟合程度越好；反之，R2的值越接近零，说明回归直线对观测值的拟合程度越差.

拟合优度公式为[3]：

2 用Python处理3个物理实验数据

2.1 光电效应测普朗克常量[5](5个点)

根据爱因斯坦的光电效应方程

可以推导出普朗克常量

根据实验数据拟合出遏止电压和频率的二元一次方程，求出斜率k，便可求得普朗克常量h=ek.

实验数据和运用Python实现梯度下降法的结果，如表1和图3所示.

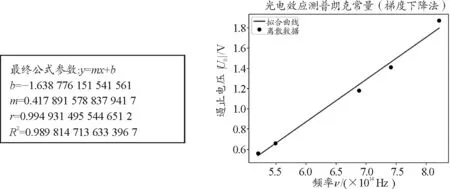
图3 Python实现遏止电压和频率一元线性拟合

2.2 光泵磁共振测朗德因子gF[4](10个点)

光泵磁共振实验中，共振条件为

hν=ΔE=gFμBB0

此式可改写为

显然，ν和B之间为线性关系.即使考虑地磁场水平分量和扫场直流分量的影响，拟合直线的斜率也不会改变.设拟合的直线方程为

ν=a0+a1B

则斜率

从而

可见只要求出直线斜率a1，代入上式便可求得gF的值.

实验数据和运用Python实现梯度下降法的结果,如表2和图4所示.

表2 光泵磁共振测85Rb朗德因子实验数据

图4 Python实现频率和水平磁场一元线性拟合

2.3 偏振光实验验证马吕斯定律[5](16个点)

马吕斯定律为Iθ=I0cos2θ.显然，Iθ和cos2θ为线性关系.大学物理实验中一般用偏振光实验验证马吕斯定律.

实验数据和运用Python实现梯度下降法的结果，如表3和图5所示.

表3 偏振光实验验证马吕斯定律实验数据

图5 Python实现Iθ和cos2θ一元线性拟合

3 结果分析和结论

本研究在实现梯度下降法时，设置步长为0.001，迭代值为75 000.我们可以根据实际情况，调大步长或调小迭代值，从而提高计算速度.

光电效应求普朗克常量中，Excel得出的拟合优度R2=0.9899，梯度下降法得到的拟合优度R2=0.989 8；光泵磁共振测朗德因子中，Excel得出的拟合优度R2=0.999 7，梯度下降法的拟合优度R2=0.999 6；验证马吕斯定律中，Excel得出的拟合优度R2=0.9991，梯度下降法得到的拟合优度R2=0.999 0.可见，Excel的R2和梯度下降法的R2结果基本一致.相关系数r和拟合优度R2在保留有效数字时，通常保留4位，而且只舍不入[7].而Excel的结果默认四舍五入，所以两者结果其实是一样的.

梯度下降法与Excel的最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要.梯度下降法是迭代求解，最小二乘法是计算解析解.物理实验数据处理中，样本量不算很大，梯度下降法与最小二乘法的计算速度大致相同，结果也相同.采用Python和梯度下降算法对我们了解深度学习和人工智能研究及处理相关数据有启发意义.