汽车发动机冷却系统散热器建模仿真与设计*

曾志新 李鑫

（广州汽车集团股份有限公司汽车工程研究院）

散热器是乘用车发动机冷却系统的核心零部件，散热器的水阻、风阻影响散热器水侧和风侧的流动性能，散热器的换热性能影响发动机的燃烧[1]。散热器的设计目标就是在匹配水阻、风阻性能的基础上，满足整车动力总成的散热需求，同时实现成本和质量的最优化。对数平均温差法计算繁琐[2]233-237，还需要查找换热器性能图表，直观性、准确度较差且研发效率较低。文献[3]从热力学第二定律出发，定义了表征换热器换热特性的3 个变量θ（冷热流体入口温度比）、R（冷热流体热容比）、NTU（传热单元数）研究它们对换热器换热性能的影响及相互作用。文献[4]对散热器自然对流状况下的传热性能及内部流动展开研究，提出了散热器消耗功率比值和内部流动及散热规律。文章基于ε-NTU的对流传热学理论建立了散热器数学模型[2]237-243，通过散热器单品性能数据拟合出散热器的换热系数，应用AMESim 软件建立整车发动机冷却系统模型，同时搭建了发动机热容模型，可以准确地仿真整车稳态工况发动机出水平衡水温和动态工况的温升曲线。这种研究方法能够显著提升冷却系统的设计效率，并获得较为准确的冷却系统性能结果。

1 经验参数方法设计

1.1 散热器经验参数方法

经验参数方法以发动机额定功率为设计工况；散热器的目标散热量的计算，如式（1）所示。依据发动机额定功率设计散热器迎风面积，如式（2）所示。散热器总换热面积的计算，如式（3）所示。

式中：Q——散热器的目标散热量，kW；

C1——传递给冷却系统的热量占燃料热量的百分数，取值范围为0.18～0.25；

ge——发动机汽油消耗率，取值范围为0.210～0.270 kg/（kW·h）；

P——发动机额定功率，kW；

hn——汽油的低热值，hn=41 870 kJ/kg；

S迎风——散热器芯体设计迎风面积，m2；

C2——散热比的面积，乘用车根据经验，取值0.07 m2/kW；

S总——散热器设计总散热面积，m2。

令Q1为散热器实际换热量；S1为实际迎风面积，为芯高与芯宽的乘积；实际总换热面积（S2/m2）的计算，如式（4）所示。当Q1≥Q，S1≥S迎风，S2≥S总时，散热器设计方案即符合设计要求。

式中：Sf——散热带散热面积，m2；

St——扁管散热面积，m2。

乘用车正常行驶过程中，额定功率点并不常用，且该工况点车速比较高，有利于散热。按额定功率点来匹配散热器，容易出现散热器的设计散热量余量偏大的问题。

1.2 经验参数设计方案

按照经验参数方法，结合某整车布置空间情况，设计散热器芯体尺寸为703 mm×440 mm×27 mm，如图1 所示。制作样件安装在工程样车上进行环模试验，低速爬坡工况下发动机出水口平衡水温只有96.8 ℃，如图2 所示。冷却系统设计目标水温为发动机出水口水温，限值为不超过115 ℃，散热器换热性能余量偏大，需要进行优化。

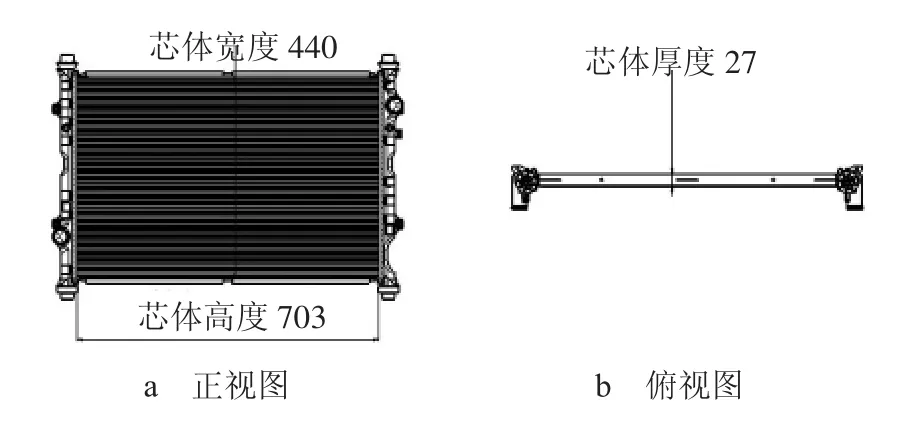
图1 某车型发动机冷却系统散热器芯体尺寸示意图

图2 某车型低速爬坡工况发动机出水口平衡水温曲线图

2 散热器及冷却系统建模分析

应用AMESim 软件，建立冷却系统模型，其中，冷却系统风侧为准三维模型，冷却系统水侧为一维模型。基于模型仿真计算，以冷却系统平衡水温最优化为目标，来设计散热器新方案。

2.1 冷却系统风侧准三维建模

建立冷却系统风侧的准三维模型，可以计算稳态和动态等不同工况，计算温升曲线。有2 种模式来计算风侧的换热，即速度模式和压力模式。速度模式以散热器前的风速分布作为输入，可以精确计算换热量；压力模式以散热器的风阻曲线和前后的压力边界作为输入，计算出平均风速，然后计算换热量。稳态工况的风速分布可以通过三维仿真计算得到，一般使用速度模式计算；动态工况的风速分布随时间和工况变化，一般使用压力模式计算。

风侧准三维模型，如图3 所示。各零部件风侧总阻力和风扇的P-V 性能曲线，如图4 所示。在怠速条件下，2 条曲线的交点为风扇的工作点，风阻为162 Pa，风速为2.89 m/s，可以满足整车的风速需求。

图3 某车型发动机冷却系统风侧准三维模型图

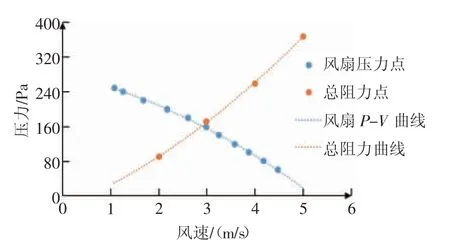
图4 某车型发动机冷却系统总阻力和风扇P-V 性能曲线图

2.2 冷却系统水侧一维建模

建立冷却系统水侧一维模型，如图5 所示。模型包含了整个冷却系统水侧回路。散热器、暖风等芯体和发动机水套水阻按台架试验得到的流量压损值进行输入，冷却管路压损按管道阻力值输入。通过测量水泵进水管和出水管的压力及流速，可以计算出水泵各流量下的扬程值。整车在各个工况下的发动机转速和功率可以通过整车动力性模型计算得出后输入，发动机在不同转速和功率下的放热量以数表形式输入，如图6 所示。温升过程是一个动态过程，需要建立发动机的热容模型，来模拟发动机本体的热量吸收过程，如图7 所示。

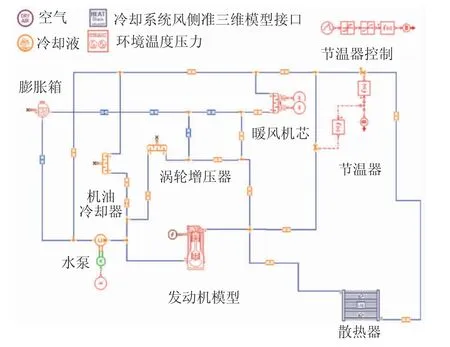
图5 某车型发动机冷却系统水侧一维模型图

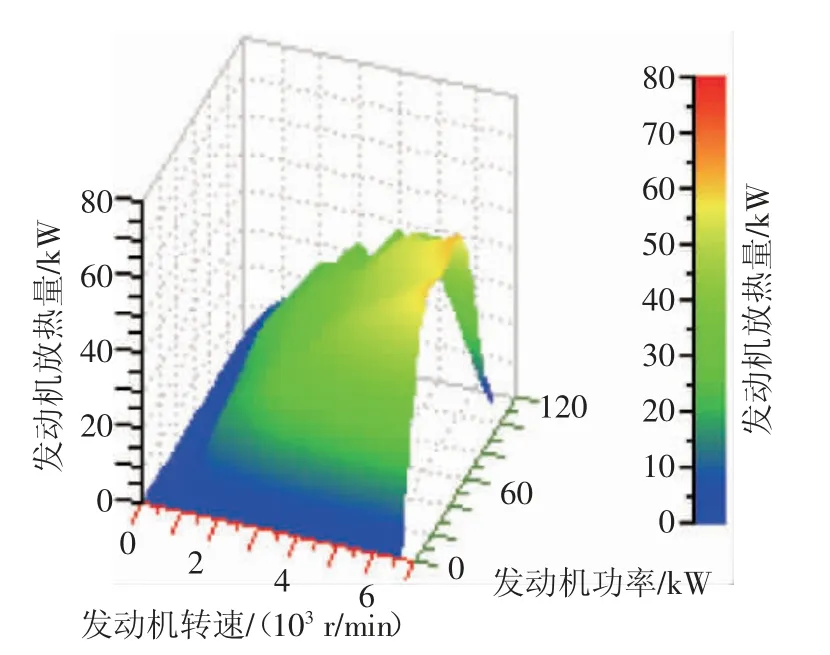
图6 某车型发动机的放热量MAP 图

图7 某车型发动机的热容模型图

2.3 散热器换热系数的数学模型

将散热器的物理模型离散为数学模型是一个难点。散热器的数学模型基于ε-NTU 方法建立。理论上，假设换热效率为100%时，只有比热容流率较小的流体能达到最大温差。实际的换热量可以用式（5）表示，换热量计算的关键是转换为求取换热效率（ε），ε 是关于努塞尔数（Nu）的函数。求取ε 的计算关键是转换为求取Nu 的拟合公式。根据散热器台架试验数据，采用雷诺数（Re）和普朗特数（Pr）对Nu 进行拟合，如式（6）所示。

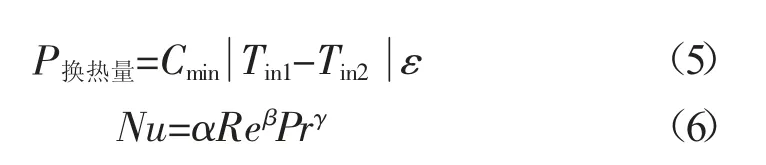
式中：P换热量——换热量，kW；

Cmin——2 个换热流体较小的比热容流率，kW/℃；

Tin1——空气的入口温度，℃；

Tin2——冷却液的入口温度，℃；

ε——换热效率，%；

Nu——努塞尔数；

Re——雷诺数；

Pr——普朗特数；

α，β，γ——拟合系数。

3 基于模型的优化设计

3.1 基于模型的优化设计方案

鉴于原方案中低速爬坡发动机出水平衡水温偏低，散热器散热余量偏大的情况，该车型散热器芯体优化方案尺寸定为703 mm×440 mm×16 mm；将散热器的芯厚降低11 mm。两方案的尺寸对比，如表1 所示。将优化方案的性能数据和几何尺寸代入模型中进行计算。

3.2 散热器优化方案换热系数的拟合

散热器优化方案的单品性能数据，如表2 所示。该性能是在液气进口温差为60 ℃条件下在换热性能试验台上按国家标准测试出来的；通过散热器台架试验单品性能数据拟合出努塞尔数的计算公式，如式（7）～式（10）所示。继而计算出散热器仿真换热效率，从而计算出仿真散热量。由散热器单品试验数据拟合得到的努塞尔数公式，可用于实际道路工况换热量的计算。

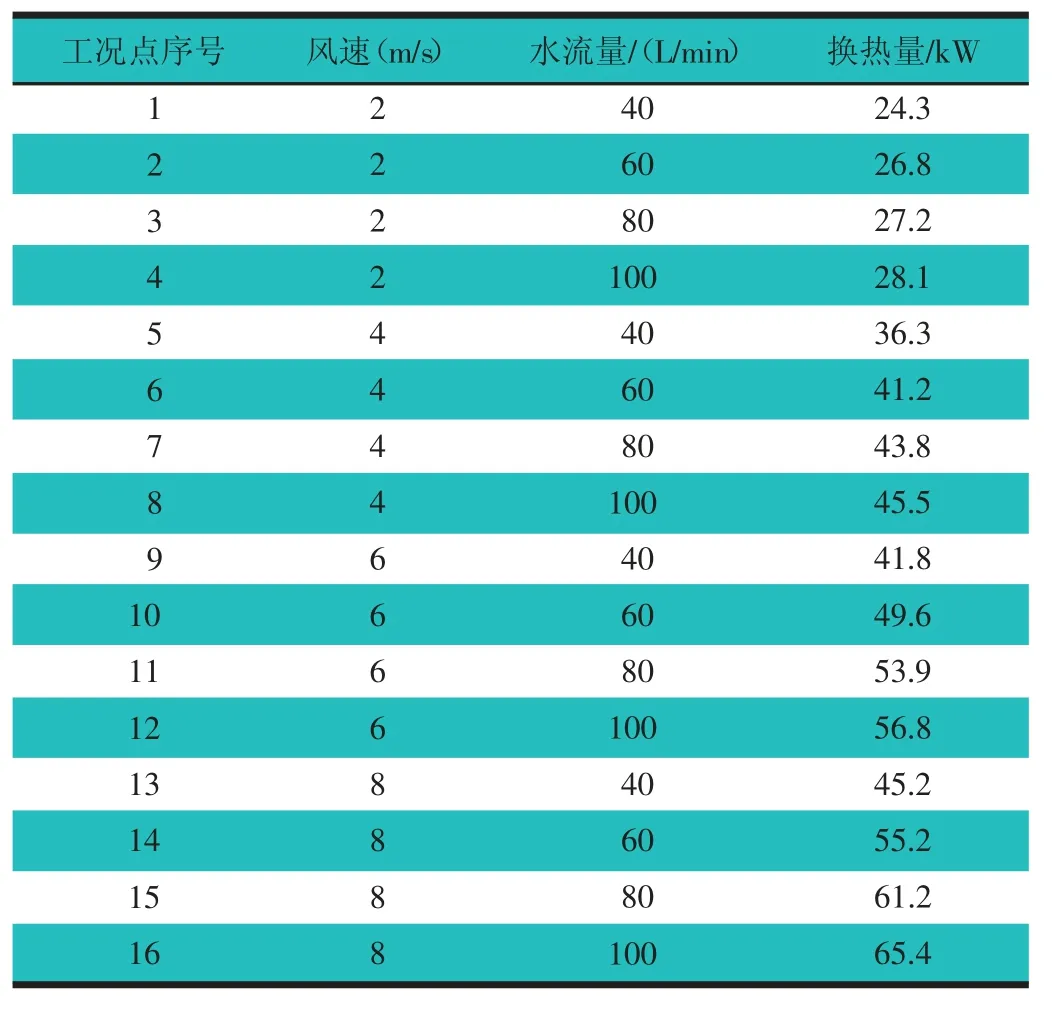
表2 某车型散热器优化方案单品性能参数表

式中：Nu1laminar——风侧层流努赛尔数；

Nu1turbulent——风侧紊流努赛尔数；

Nu2laminar——水侧层流努赛尔数；

Nu2lturbulent——水侧紊流努赛尔数。

3.3 极限稳态工况仿真和试验结果分析

低速爬坡工况和高速爬坡工况对整车冷却系统的考核比较严苛，工况参数，如表3 所示。由于这2 个工况是稳态工况，车速和发动机转速稳定，所以散热器风侧的流量用速度模式计算，散热器前的风速、风温分布由三维CFD 仿真分析结果作为输入；建立该车型冷却系统水侧一维模型，并将模型参数输入，进行模拟计算。

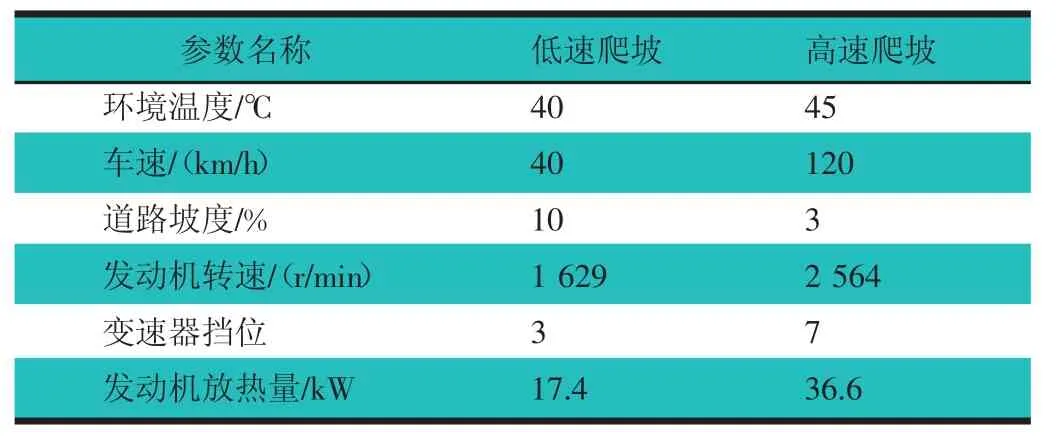
表3 某车型发动机冷却系统极限稳态工况试验条件参数表

发动机出水口平衡水温的仿真结果，如图8 所示。低速爬坡的发动机出水口平衡水温为113.4 ℃，高速爬坡时为114.8 ℃，符合设计水温限值（115 ℃）要求。

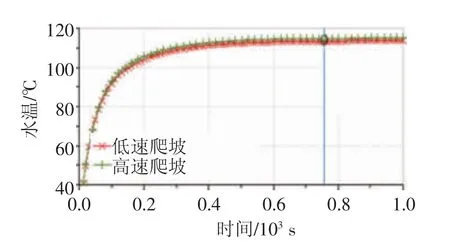
图8 某车型稳态工况发动机出水口平衡温度仿真曲线图

将新样件装车进行环模试验，实车试验结果，如图9 所示。优化方案中低速爬坡的发动机出水口平衡水温为113.1 ℃， 高速爬坡为115.0 ℃，符合设计水温限值（115 ℃）要求。仿真与试验对比，如表4 所示。低速爬坡平衡水温误差为0.26%，高速爬坡工况误差为0.17%，说明仿真结果较为准确。

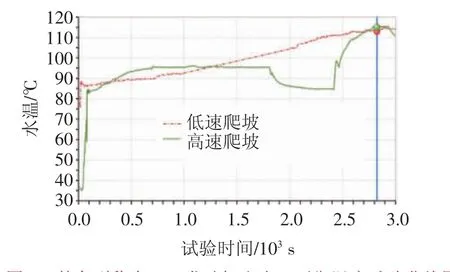
图9 某车型稳态工况发动机出水口平衡温度试验曲线图

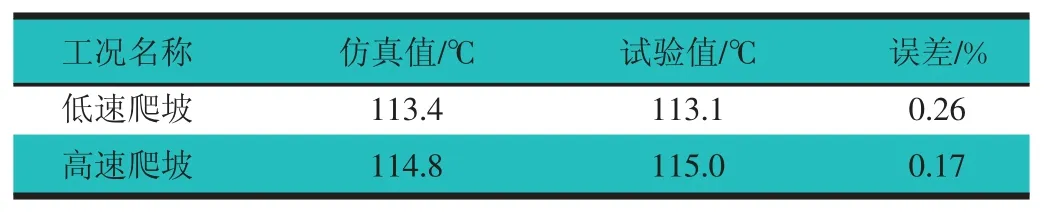
表4 发动机出水平衡温度仿真与试验对比表

基于模型以冷却系统平衡水温为目标设计的散热器新方案，相比于芯厚27 mm 的原散热器，低速爬坡的平衡水温提高了16.3 ℃，同时满足115 ℃的设计限值要求，散热器质量降低了1.2 kg，实现了散热器的轻量化目标和最优的冷却系统性能。

4 WLTC工况仿真计算和试验验证

国家第六阶段排放的标准工况为WLTC 工况，车速不断变化，属于动态工况，用压力模式来计算散热器风侧的平均风速。建立冷却系统风侧准三维模型和水侧一维模型，进行仿真计算。

仿真和试验所得到的发动机出水温度温升曲线，如图10 所示，两者的一致性较好，循环进行至443 s，暖机完成，水温达到80.16 ℃。循环结束时发动机出水平衡水温在84 ℃，试验水温与仿真水温全工况相差值在2 ℃以内。

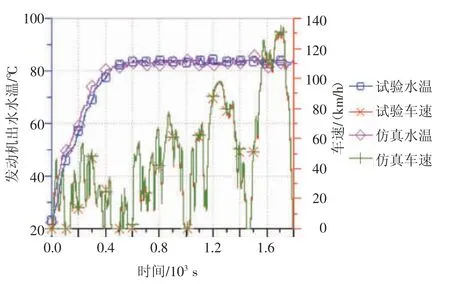
图10 发动机温升曲线仿真与试验对比曲线图

5 结论

文章研究了以整车实际道路工况的冷却系统最优性能为目标，基于仿真模型的散热器设计方法。对比以发动机额定功率点散热量为目标的经验参数方法，设计方法更加精确，设计效率高，解决了散热器散热余量偏大的问题，同时实现了冷却系统的轻量化目标。文章建立的模型具有一定的拓展性，后期可以耦合空调等其他系统进行整车热管理分析和能量流动分析。