基于跳回归的高频杠杆交易策略研究
朱 敏,李震巍,宋玉平
(上海师范大学 商学院,上海 200234)
一、引言
伴随着资本市场交易制度的创新、交易工具的完善,近年来国内量化交易蓬勃发展。由于与西方成熟资本市场存在较大差异,国外成熟的量化交易策略并不能直接照搬,仍需要结合中国资本市场的特征选择、调整。因此,相关的理论研究尤为重要。
基于两个资产价格变动的同步性构造配对交易策略是量化交易设计的重要方向。其中一个投资组合的设计就是配对资产杠杆交易策略。所谓配对资产杠杆交易策略,具体为:在两个资产短时出现同步上涨的机会窗口下,投资期初构造一个投资组合,通过卖空资产暂时借入资金构造空头头寸,并利用借入资金买入另一个资产构造多头头寸。在投资期末,投资组合中多头位置的资产卖出获利,空头位置的资产平仓止损。如果多头位置的资产涨幅超过空头位置的资产涨幅,那么上述投资组合多头头寸的获利在弥补空头头寸损失的同时,还能获得等于两个资产涨幅差额的回报。这个设计的目的在于构造了一个“无本金投入”策略,通过杠杆提高卖空资产的规模,就可以放大投资回报。
在高频交易条件下,资产价格经常出现短时跳跃现象,而关联资产也会在跳跃期间出现价格变动的同步性。显然,只要合理利用跳跃的瞬时同步特性,就能够构造高频配对交易策略。又由于短时跳跃频率的密度要高于低频交易,因此配对资产杠杆交易策略在高频交易条件下将是一个理想的投资选择。
本文涉及的研究文献集中在配对交易策略以及高频跳跃特征这两个方向。就配对交易策略研究而言,在Bondarenko定义了统计套利之后[1],Vidyamurthy提出了以相对定价概念的配对交易思想,以协整关系构建统计套利策略[2]。Elliott等人将马尔可夫链引入配对交易策略中去,进行择时的优化[3]。胡伦超等在中国融资融券的实际背景之下,采用协整和距离配对法进行了配对交易策略的研究[4]。在考虑金融时间序列的动态时变、非对称和非线性相关的特征后,沈银芳等利用时变混合Copula模型进行配对交易策略的构建发现在高频下策略的盈利性表现更好[5]。综合来看,以往的文献鲜有从多资产跳跃瞬时同步性的特征构造配对交易策略。
另一方面,高频状态下资产跳跃的相关研究由理论和运用两部分构成。就跳跃过程的理论研究而言,Aït-Sahalia将跳跃分为泊松跳跃和列维跳跃,即按照跳跃幅度的大小将前者划分为大跳后者划分为小跳[6]。对于跳跃现象的识别,应用最为广泛的非参数分析模型是Barndorff-Nielsen和Shephard提出的双幂变差方法(BV)[7-8],其后Ait和Jacod根据分布特性与跳跃特性的关系提出了阀值估计方法(TE)[9]。王春峰等对两种方法对比发现BV法更适用于噪音较低的有限跳跃现象的识别,TE在价格非连续下的不同跳跃现象有较为有效的识别作用[10]。
基于以上跳跃的理论研究,同时期出现大量利用理论模型对资产跳跃变化特征进行分析的运用性研究。覃邑龙和胡小军提出瞬时波动法和QQ检测法对跳跃现象进行检测,并对上证综指与其八只股票的跳跃情况进行了比较分析[11]。对于跳跃过程关系的研究,曾昭法和左杰对比上证综指和恒生指数跳跃现象发现,沪市的跳跃行为更容易引起港市的波动[12]。陈琳和乔志林于半鞅过程,结合非参数统计推断,利用幂变差的渐进性构造统计量,用以对跳跃现象的识别[13]。殷炼乾等对中国资产价格的跳跃现象进行研究,发现中国证券市场下跳现象多余上跳现象[14]。
本文根据高频杠杆交易策略的实施条件,从偏离性和稳定性两个角度比较分析了不同类型行业指数在综合指数跳跃状态下跟随变化的特点,筛选出理想的行业,最后利用样本外数据进行稳健性检验,进一步论证策略的可行性。
二、研究设计
(一)高频杠杆交易策略
如果指数和行业个股的收益率存在线性关系Δy=1.1Δx,那么在投资中可以构造一个配对交易策略,即通过做空指数借入一个单位的资金,然后拿该笔资金做多行业个股,持有一段时间以后多头获利了结,空头平仓止损。由于个股和指数涨幅存在非对称性,假设指数上涨1%,则个股上涨1.1%,平仓指数空头即可获得0.1%的无本金投入收益。现实中,基于该策略并利用卖空交易的杠杆可以放大最后的收益。
这一策略实现的关键在于必须找到与指数高度同步的个股配对,而方向错配或低同步性都会影响收益,甚至产生损失。低频交易条件下,指数和行业个股的收益率并不能满足高度线性,即单一事件下行业个股并不一定跟随指数同向变动,该策略不具备可操作性。但在高频交易环境下,情况就发生了变化。高频交易条件下市场存在不少脉冲式跳跃,指数一旦出现跳跃,短时之内行业个股往往会跟随跳跃。现有文献表明,跳跃状态下行业和指数的价格走势会出现瞬时同步性,也就是说在发生跳跃的时间窗口内两者之间存在高度线性的同向变动关系。意味着高频环境下具有实施以上配对交易策略的条件。
进一步考虑操作细节,配对资产跳回归系数的性质是整个策略运行的核心,跳回归系数的偏离性和稳定性是配对资产筛选的准则:
首先,跳跃幅度的偏离性。即跳回归系数偏离1的程度,如果偏离程度越大,两个资产变动幅度的非平衡也就越突出,那么杠杆交易的收益就越理想。此外,还需要考虑跳回归系数是大于1还是小于1,这关系着两个资产的交易方向选择。在上跳方向上,需要做空涨幅小的资产,做多涨幅大的资产;在下跳方向上,需要做多跌幅小的资产,做空跌幅大的资产。
其次,跳回归系数稳定性。即跳回归系数在一段时间性质变化不大,特别是不能出现跨越1的偏离。因为对于本文设计的杠杆交易策略,如果跳回归系数的预期大于1(小于1),而实际系数小于1(大于1),就会造成事前设定对两个资产做多做空的交易操作与实际要求的交易方向完全相反,产生亏损。
因此,有必要从跳回归系数的角度对资产配对进行研究,从而找出实施高频杠杆交易策略理想的资产配对。本文从沪深300指数和相关行业指数入手,通过对两者之间跳回归系数性质的研究,找出适用该杠杆交易策略最理想的行业。
(二)跳回归模型
跳回归系数是资产选择、策略实施的核心要素,因此首先定义基于跳扩散过程的跳回归模型。
金融市场中,扩散模型可以表示为:

(1)
(2)
其中,将Y和Z定义成概率空间(Ω,F,(Ft)t≥0,),表示为X=(Z,Y)T,2表示非零实数集。漂移系数bt∈2;扩散系数σ2∈M2,M2是2×2的矩阵空间;W是二维标准布朗运动;δ=(δZ,δY)T是一个可测函数:Ω=+×→2;μ是一个泊松随机测度;Jt=(JZ,t,JY,t)T,JZ和JY分别是Z和Y的跳跃分量;时间t上X的协方差矩阵定义为
高频数据允许对跳跃进行鲁棒的非参数估计。本文针对资产价格过程(Yt)t>0和总风险因素(Zt)t>0,研究两者之间的关系。具体来说,分析研究τ∈T(T是Z的跳跃时间集合)时的ΔYτ和ΔZτ之间的关系βτ:
ΔYt≡Yt-Yt-,t≥0
(3)
ΔZt≡Zt-Zt-,t≥0
(4)
(5)
在没有任何条件限制的情况下,βτ是随机的且随着跳跃的变化而变化。但是在许多情况下,Y和Z的跳跃之间的关系可以通过一个已知有限维参数的函数来获取。最常见的如下线性函数:
ΔYt=βΔZt+Δεt,ΔZtΔεt=0,t∈[0,T]
(6)
本文将此线性回归函数作为跳回归模型对问题进行分析研究。
(三)跳跃点识别
在实际运用中研究跳回归模型的跳回归系数,前提条件是对资产价格变动过程中跳跃点进行识别,这样才能筛选出跳跃样本。为了识别跳跃点需要设置一个阈值序列vn,本文考虑到ct矩阵的时变性,采用双幂变差估计构建vn:
(7)
(8)

(9)
对于每个p∈P,P可能是一个随机的集合,i(p)是唯一的随机指数,τp∈((i-1)Δn,iΔn],在此设置:

(10)
L(D)≡{i(p)∶p∈PD}
(11)

(四)跳与非跳状态的对置系数检验
由于跳跃非连续且稀疏,同时跳回归系数又存在时变问题,在实际运用中,利用跳跃样本数据估计当前状态跳回归系数的性质就可能面临一定的困难。一种解决方案就是使用非跳状态下的数据去进行推断。是否可行,就需要首先分析跳回归中ΔYt和ΔZt之间的跳回归系数是否与非跳状态下的回归系数存在差异,如果存在那么差异是否统计显著。
为了分析跳跃阶段中跳回归系数与其他情况下的差异性,我们构造对置检验,即我们计算出一段时间内非跳样本的回归系数,然后建立原假设,原假设认为跳状态下的回归系数与非跳样本下求得的回归系数无差异,运用Wald检验来进行有条件约束的检验。
对于n维随机变量x,如果x~N(μ,∑),∑为满秩的,则:
(x-μ)′∑-1(x-μ)~N(0,σ2)
(12)
考虑一般回归模型:
y=f(x,β)+u,u~N(0,σ2)
(13)
对参数的约束可以写为:
H0:g(β)=0
(14)
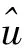
(15)
(16)
(五)跳回归系数稳定性检验
另一个重要问题就是跳回归系数的稳定性,即在多长的时间间隔区间内性质保持不变,这对策略的可靠性至关重要。对于跳回归系数稳定性的检验,本文基于方法,固定区域D对β的稳定性进行检验。在区域D中,Z至少有两个标记的跳跃点,即|PD|≥2。在形式上,检测问题取决于样本落在以下哪条路径:
(17)
由Cauchy-Schwarz不等式可知,f(ΔZτp)=βΔZτp等价于半正定矩阵Q(D)的奇异性。因此,本文通过对det[Q(D)]=0的单边检验来进行对跳回归系数稳定性检验。构造Q(D)的样本相似估计量:

(18)

(19)
(20)
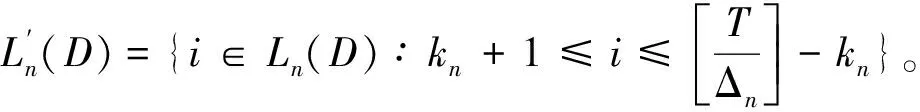
(21)
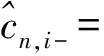
(22)
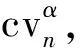
(23)
计算:

(24)

稳定性检验可以定义为已经实现的跳跃相关来等价给出:
(25)
可以观察到:
(26)
三、实证结果分析
(一)数据选取与说明
本文从wind数据库系统选取自2014年1月2日至2017年12月31日4年的5分钟高频数据。其中包括沪深300综合指数,以及能源、材料、工业、消费、医药、金融、公用等行业指数,总计340 288条收盘价数据,通过计算对数收益率把非平稳数据转换为平稳数据进行分析。利用R语言软件对高频数据预处理并对检验模型编写实现程序。
(二)实证结果
从年份和时频两个维度,基于阈值的方法检测跳跃点。在检测出跳跃点后,首先对跳回归系数的偏离性质进行分析,筛选出符合高频杠杆交易策略的理想标的。第二部分检验跳与非跳条件下回归系数差异性,研究非跳与跳条件下回归系数关联性的线索。第三部分研究跳回归系数时变的特点,找出跳回归系数的稳定性规律。
1.跳跃点统计特征概述。首先,我们利用跳跃点甄别函数分别搜索了2014年至2017年5分钟和10分钟两个频段沪深300指数的收益率,提取了全部的跳跃点,并对这些跳跃点进行描述性统计分析,如表1所示。

表1 沪深300指数收益率跳跃点统计特征
从均值的特征看,5分钟收益率的均值基本在0附近波动,其中2016年的均值为-0.431,相对其他年份偏离0值的程度最大,且四年中跳跃点最大值为1.697,最小值为-2.542,均出现在2016年。从标准差角度看,无论是在5分钟数据还是10分钟数据,跳跃点在2016年波动最为剧烈。所有这些现象从多个角度反映了2016年初中国证券市场因熔断引起股灾,股灾对整个市场的影响。也提示在研究过程中对异常年份2016年要区别对待。
5分钟数据和10分钟数据的偏度数值均为负值,说明跳跃发生的非对称性,下跳点的跳跃幅度普遍大于上跳点,这和发达国家市场的高频数据特征一致。
2.跳回归系数分析。本文在检测出沪深300指数收益率的跳跃点之后,将其作为自变量引入跳回归模型,并将证券市场的行业指数收益率作为因变量引入模型进行回归。按照整体数据、跳跃数据、上涨数据、上跳数据、下跌数据、下跳数据的顺序进行回归分析,得到表2。
首先分析不同行业的偏离系数。从表2最后两列历年平均的结果看,医药行业的偏离程度最大,为0.28。其次是公用和能源,大约为0.24。而且医药和公用的跳回归系数明显小于1。
进一步分析上跳情形下的偏离情况。从表2最后两列的结果看,依然是医药行业的偏离程度最大,为0.362。其次是公用和金融,大约为0.29。进一步分析这三个行业跳回归系数的平均值可以发现,医药和公用两个行业的跳回归系数小于1,而金融行业的跳回归系数则大于1。
下跳情形下结果略有不同。如表2所示,公用的偏离程度最大0.341,金融的偏离程度次之0.257,医药居于中等水平,大约是0.171。
综合来看,医药、公用、金融等三个行业的跳回归系数,4年的平均偏离度最高,是策略理想的备选。
进一步观察系数的时变特征。可以发现一个显著的规律是:如果特定行业在特定阶段受市场资金亲睐,存在持续买入预期,则高频下行业收益率对综合指数收益率向上变动的响应更为敏感,表现为上跳系数普遍大于上涨的系数,而下跳的系数小于下跌的系数。
此外还存在行业对指数反应敏感度反转的现象。2014年上跳比下跳敏感程度强的行业在2015年有所反转,而下跳比上跳敏感程度强的行业在2015年也有所变化。而在2016年,各行业上跳的敏感程度明显高于下跳的敏感程度。与之相反的是在2017年,行业普遍存在下跳敏感程度明显高于上跳的敏感程度。显然,这一现象与行业板块效应基本一致。对于强势行业板块,同一时期上跳的反应强于下跳;而弱势行业板块恰好相反。

表2 全样本跳回归系数偏差程度

表3 跳跃与非跳跃阶段的系数差异性Wald检验
3.跳与非跳状态下的比较分析。下面我们进一步比较跳过程下与非跳过程下回归系数是否存在差异,且这种差异在统计上是否显著。我们使用系数对置的思路对原假设进行Wald检验,据此进行分析。原假设分别为上涨(下跌)全体数据的回归系数与上跳(下跳)数据的回归系数没有差别,上涨(下跌)剔除跳跃点数据的回归系数与上跳(下跳)数据的回归系数没有差别。检验结果如表3所示。
根据表3的数据可以看出,上跳与上涨全样本数据的回归系数以及上跳与上涨无跳样本数据的回归系数并不是在各个行业和每年都有明显差异。在2014年材料、工业和医药行业的跳回归存在差异,到了2015年各行业的跳回归无明显差异,在2016年能源、医药和公用行业的跳回归存在差异,2017年能源、材料和消费行业的跳回归存在差异。
而下跳与下跌全样本数据的回归系数以及下跳与下跌无跳样本数据的回归系数相比上跳的各种情况则有明显变化,可以发现下跳的差异性更为显著。尤其在2015年和2016年,下跳的差异性在各个行业都存在,但是到了2017年下跳差异性显著的只有医药行业。
综上来看,各个行业跳与非跳不同年份的反应差异与板块强弱基本相关。需要特别指出的是,虽然跳与非跳状态下的反应强度会有一定区别,但基本是两者同向的,且非跳状态下行业指数对指数跳跃的反应包含着板块的强弱信息,这意味着一定时期非跳状态下的信息仍然可以为我们判断跳状态下的杠杆比例提供参考。

表4 不同时频下行业跳回归系数的稳定性检验
4.跳回归系数稳定性分析。为了确定跳回归系数的稳定性,本文按年度对不同行业的跳跃系数进行了不变常数检验。原假设为跳回归系数是稳定的,即回归系数为常数。表4列出了不同行业不同年份下回归系数稳定性检验的结果,其中Qn是稳定性检验的统计量,表4中对5分钟数据和10分钟数据都做了分析,便于比对判断结果是否稳定可靠。
根据表4的数据来看,各行业跳回归系数的稳定性在各年表现有所不同,其中医药行业5分钟数据的跳回归系数除在2016年外,都在5%显著性水平下接受原假设,即跳回归系数不随时间变化。分析其原因是医药行业作为防御性板块,对市场总体表现的反应较为稳定。
为了验证医药行业跳回归系数稳定性的趋势,做出10分钟数据跳回归系数稳定性检验。从表4的数据可以看出,医药行业在降低时频的情况下仍然具有稳定的特征。
由以上的综合分析,所有行业中最理想的投资选择是医药行业,不仅仅其偏离度较大,更重要的是跳回归系数最为稳定。其次是公用、金融行业。
5.稳健性检验。为了验证上述理论分析可靠性,即利用理想行业的标的资产构造高频杠杆交易策略是否能够确保获利最大化。我们先对不同行业进行了策略回测,然后又进行了样本外检验。在实施策略的时候,交易窗口是盈利大小的关键因素。参考以往的文献,大部分高频交易持有时间的经验设定在1、5分钟或10分钟。因此本文在实施回测时,采用经验时间5分钟的设定。虽然交易窗口会影响到策略的盈利,但如果交易标的的特性稳定,回测的结果不影响对有效性的定性判断。当然最优交易窗口的选择是实践运用的重要环节,这也将是本文后续研究的重要内容。
稳健性检验的回测和样本外检验,策略具体的操作设定为:首先,根据前一个季度的回归系数偏离方向,确定多头和空头的资产选择。一旦检测到5分钟出现跳跃,激活杠杆交易策略,构造一个投资组合,执行买入和卖出操作,开始短期投资。然后持有投资组合5分钟后,结束短期投资。最后计算投资期间的累计收益率。
结果如表5所示,如果在不同年份下实施高频杠杆交易策略,只有工业、医药和公用在样本期累计收益率都为正。其次,如果按照历年平均收益率排名,医药、公用、消费分列前三,这与我们研究行业指数跳回归性质得到的结果一致。
进一步,我们运用2018年1-6月的样本外数据进行样本外检验。结果如表5所示,我们以医药、金融、公用三个行业指数作为候选组,能源、材料、工业和消费行业指数作为对照组。在投资期间,共发生上跳5次,下跳2次,一共7次投资。就偏离系数看,医药、公用两个行业最大。可以看到医药的累计收益为0.599,在7个行业中最高,其次是公用,收益为0.441。样本外数据的回溯测试显示我们行业筛选是有效的。医药和公用两个行业,是比较理想的运用基于跳回归的高频杠杆交易策略的对象。

表5 策略回测及样本外检验
四、结论
本文基于高频交易跳跃现象中资产配对产生的瞬时同步性特征,提出基于跳回归的高频杠杆交易策略。针对策略实施的条件,研究配对资产跳回归系数的性质,通过考察综合指数与行业指数配对之间的偏离性和稳定性,提出有效实施策略的行业选择。
实证结果中,各个行业跳回归系数特征显示,医药、公用、金融等三个行业的跳回归系数,4年的平均偏离度最高,是策略理想的备选。此外不同时期行业的跳回归系数板块效应明显。即对于强势行业板块,高频下行业收益率对综合指数收益率向上变动的响应更为敏感,表现为上跳系数普遍大于上涨的系数,而下跳的系数小于下跌的系数。弱势行业的情况则恰好相反。
其次,跳与非跳状态下的回归系数的比较结果显示,跳与非跳状态下的反应强度会有一定区别,但基本是同向的,且非跳状态下行业指数对指数跳跃的反应包含着板块的强弱信息,这意味着一定时期非跳状态下的信息仍然可以为我们判断跳状态下的杠杆比例提供参考。
最后,进行了跳跃系数的稳定性检验,结果发现所有行业中最理想的投资选择是医药行业,不仅仅其偏离度较大,更重要的是跳回归系数最为稳定,公用、金融行业的稳定性仅次于医药行业。

