燃烧反应机理全局性简化及骨架机理优化

林圣强，谢 鸣，王佳星，周伟星，杨 斌

燃烧反应机理全局性简化及骨架机理优化

林圣强1，谢 鸣1，王佳星2，周伟星1，杨 斌2

(1. 哈尔滨工业大学能源科学与工程学院，哈尔滨 150001；2. 清华大学燃烧能源中心和热科学与动力工程教育部重点实验室，北京 100084)

燃烧基元反应速率系数存在着一定的不确定性，会影响各基元反应对燃烧特性参数的贡献，传统图解简化法统计基元反应中各组分贡献大小也会受此影响，使组分之间的耦合强度存在着一定的不确定性．为此拟开展基于燃烧反应动力学速率系数不确定性下的机理简化和优化．首先在速率系数不确定性参数空间内均匀采集1000个可能性详细机理样本，然后应用直接关系图解法(DRG)对机理样本进行简化，并对排除的组分进行统计和排序，最终根据概率大小削减模型；其次应用全局敏感性方法判断其重要反应机理，对其中较为灵敏的反应进一步优化，最终得到可以预测相对准确的简化机理．

全局敏感性分析；DRG方法；不确定性分析；最小二乘法

为了更加真实地掌握发动机燃烧过程中的释热规律和精细流场结构，也为了更好地设计发动机、组织燃烧、控制污染物的反应路径，数值计算的作用越来越重要．然而包含众多组分和基元反应的机理给数值计算带来巨大挑战，庞大的机理带来高度的非线性和多尺度性，不仅影响整体计算过程的收敛速度，也容易导致求解发散，很不利于研究的开展．在数值计算研究发动机燃烧过程中，可能不需要反应机理能在非常宽的范围下进行精确预测，也不关注那些质量分数低于10-5及以下的组分，此时机理的简化就变得非常必要，也是当今非常重要的研究领域[1]．

在机理简化方面，有许多简化手段被提出来缩减机理的尺寸，从简化的目标出发可简单分为两类：一种类型为简化基元反应的尺度，像SA、PCA等[2]；另一种类型为简化反应动力学模型的组分，像DRG、DRGEP、PFA等[3-5]．在简化大型燃烧详细机理时，这两类方法通常相互配合使用，第一阶段可先通过筛选组分的方法简化模型，后通过第二类方法消除一些冗余反应机理，以达到精简反应模型的目的．虽然上述的简化手段可以较大幅度简化机理，但所得到的简化机理对于数值计算模拟过程还存在两个问题：第一，目前的简化机理对于一般计算机模拟发动机燃烧过程来说还是比较困难，特别是对大组分的机理，因此迫切需要新的简化策略来缩减反应动力学机理模型；第二，这些方法都没考虑速率系数的不确定性对机理的影响，这可能导致不重要的反应和组分被强化，重要的反应和组分被弱化，并会严重影响表征燃烧过程中重要的基元反应和主要的反应路径，越是大幅度简化机理越会使得机理的不确定性加剧，越是容易得到错位的简化机理[6]．燃烧机理存在着很大的不确定性会对简化过程造成重要的影响，特别是重要组分和反应的鉴别，因此本文开展速率不确定性下的机理简化.

如果反应机理不需要在很宽的范围内准确预测燃烧特性参数，那么削减少量的反应机理可能不会对机理预测能力产生影响，但是如果机理进行较大幅度地削减，那么简化机理就很难能准确预测燃烧特性参数．因此，为了精简模型，通过优化速率系数来提高简化机理的预测能力受到越来越多的学者关注[7]．本文采用最小二乘法(LM)的优化算法对简化机理进行优化．不过优化众多参数会使优化算法效率低下，而且容易陷入局部最优解．为了减小所优化参数的量，本文先对燃烧机理进行全局敏感性分析，选择较为灵敏的基元反应进行优化．全局敏感性分析复杂模型的方法有很多，像傅里叶全局敏感性方法FAST[8]，Sobol[9]、RS-HDMR[10]等．这些方法都已经被证明是非常有效的手段去诊断反应动力学模型．但FAST方法可以在较小的样本数下评价不确定性参数对模型输出的影响，并可以得到分辨正负的全局敏感性系数．因此本文选择FAST方法来研究速率系数的不确定性对燃烧重要参数的影响，鉴别起重要作用的基元反应，为机理优化提供合理的参数量，以缩减模型优化过程的时间消耗．

为了得到可靠和精简的简化机理，本文开展了基于速率不确定性下的机理简化方法，指出目前传统DRG方法在简化过程中存在不精确地删除组分的现象，即不能精确地找到强耦合的组分．基于目前简化手段缺陷，本文开展一套方法得到预测能力高的简化机理，包括考虑速率系数不确定性的机理简化、应用全局敏感性方法判断重要的基元反应，以及应用优化算法优化模型[7]．

1 考虑速率系数不确定性下的机理简化和 优化

为获取精简和可靠的简化机理，本文主要思想如下：首先考察速率不确定性的机理简化的方法；其次应用全局敏感性分析方法筛选重要的基元反应；最后通过优化基元反应速率的方法提升简化机理的预测能力．

1.1 考虑速率系数不确定下的机理简化

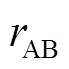
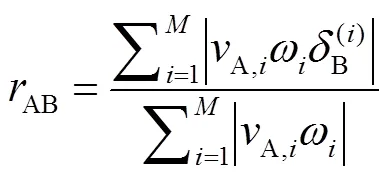
其中：

DRG方法应用比较巧妙的方式表达出组分B所参与所有的基元反应对A组分的贡献．通过公式(1)就可以知任意两个组分之间依赖程度，但还不能获取一类强耦合组分的集合．

DRG的第二个步骤是应用搜索算法查找强耦合组分的集合，所用的方法为深度优先算法(DFS). DFS是有方向性的搜索算法，它从目标组分(通常是指反应物和生成物)出发，沿着它相关联的组分逐一搜索下去，得到目标组分下的一个图形网络．DRG方法设定了一定阈值，组分之间是否耦合起来取决于阈值大小．通常情况下阈值越大，与目标组分所搜索得到的图形网络越小，简化机理模型也越小，但简化模型预测精度会变差．

由于基元反应速率系数很难精确获取，即使对于最简单的基元反应，其不确定性仍然保持在±10%到±30%之间．仅依赖名义上详细机理进行简化，并不总能获取最优的结果，而考察不确定性下的机理简化很有利于获取代表整个参数空间内最优的简化机理．

为了获取速率参数空间内最优简化机理，首先在参数空间内均匀采样1000个点，构成1000个详细机理；接着应用DRG方法对这些详细机理进行简化，得到1000个简化机理．通过概率统计方式统计被排除组分的概率，最终依据该概率数据对该模型进行削减．

1.2 傅里叶全局敏感性方法

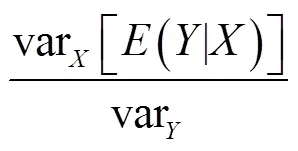
在积分公式(6)时，在输入参数曲线上取下采样点数N来近似整个曲线积分，采样点在曲线上按s＝2π/N(＝1，2，…，N)取点，但N大小是由最大采样频率和采用多少个高次谐波数决定的，N＝2max，那么公式(6)离散得：

第输入参数对第输出敏感性定义为S：

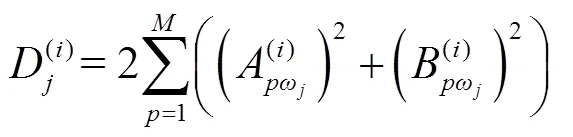
1.3 优化方法

燃烧模型包含众多的基元反应，这些基元反应的速率是通过阿累尼乌斯方程计算，但阿累尼乌斯中的指数项使得模型出口特性参数关于速率系数是强烈的非线性，精确模型或优化模型非常困难[11]．由于模型出口的特性参数与速率系数的特殊关系，本文选择最小二乘法的优化算法，在较小的参数空间内寻找最优值，保证重要组分和重要反应与原机理一致．本文给的目标函数如式(11)所示：

2 结果和结论

2.1 考虑速率不确定性下的机理简化

为了方便讨论和说明，本文所应用的燃烧机理为不考虑氮氧化物生成的GRI3.0燃烧机理，包含35个组分和217个反应[3]．应用DRG方法简化反应机理的目标是简化机理可准确预测点火延时时间，考虑的计算初始条件为：压力0＝0.1MPa，当量比＝1.0，温度范围为0＝1000～1600K．传统DRG方法得到的非强耦合组分如表1所示，以及不同阈值下简化机理所预测的点火延时时间如图1所示．

表1 不同阈值下DRG方法排除的组分

Tab.1 Removed species by the DRG method under different threshold values

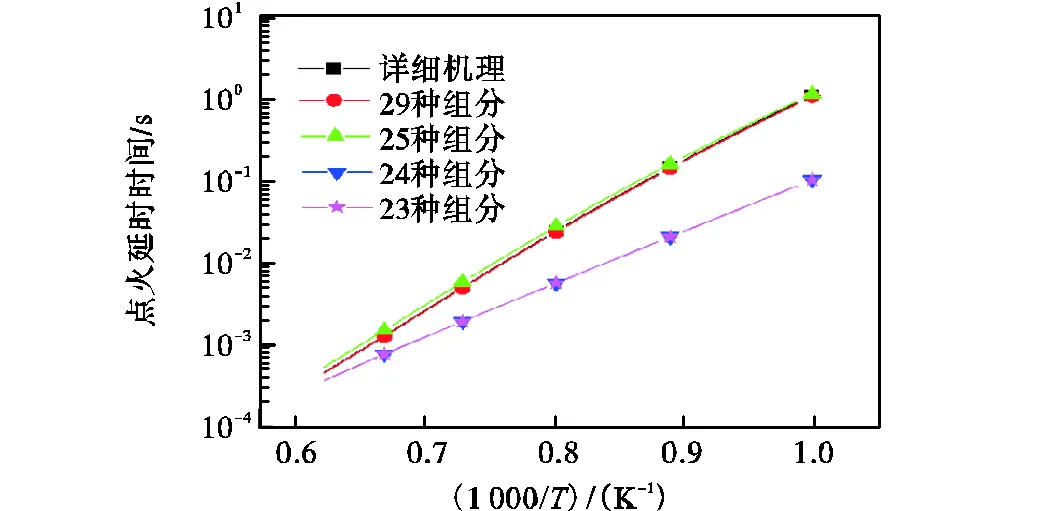
图1 传统DRG方法简化机理和详细机理下所预测点火延时时间

从表1和图1中可以看出，在DRG简化机理模型时，29组分和25组分的简化机理可以准确地预测点火延时时间．但增大削减规模后，24组分的简化机理就不能很好预测点火延时时间．从表1中还可看出，25组分的简化模型比24组分的简化模型多了C2H6组分，但C2H6影响着39个基元反应．如果删去C2H6组分，就会影响多达39个的基元反应速率，对模型影响巨大，所以24组分的模型预测能力会急剧下降．从图中还可看出，25组分的简化机理是传统DRG方法的极限．如果想继续删去组分，就必须依靠优化算法优化速率系数来提高简化机理的预测 能力．

上述简化过程是不考虑速率系数不确定性的影响，速率系数不确定性的存在使得燃烧机理具有比较大的敏感性，那么传统方法简化机理将会导致简化机理存在更大的不确定性，可能会出现非强耦合组分被强化、强耦合组分被弱化的现象．为了考察机理的不确定性对简化机理的影响，本文应用概率的方式来统计非耦合组分的概率，如图2所示．为了区分传统DRG方法，记此方法为全局DRG(GDRG)方法．GDRG方法分析过程的主要操作如下：首先在不确定性速率系数的参数空间内均匀采样1000个样本点；然后应用DRG方法对1000个燃烧机理模型进行简化，从而得到每个非强耦合组分概率，如图2所示．

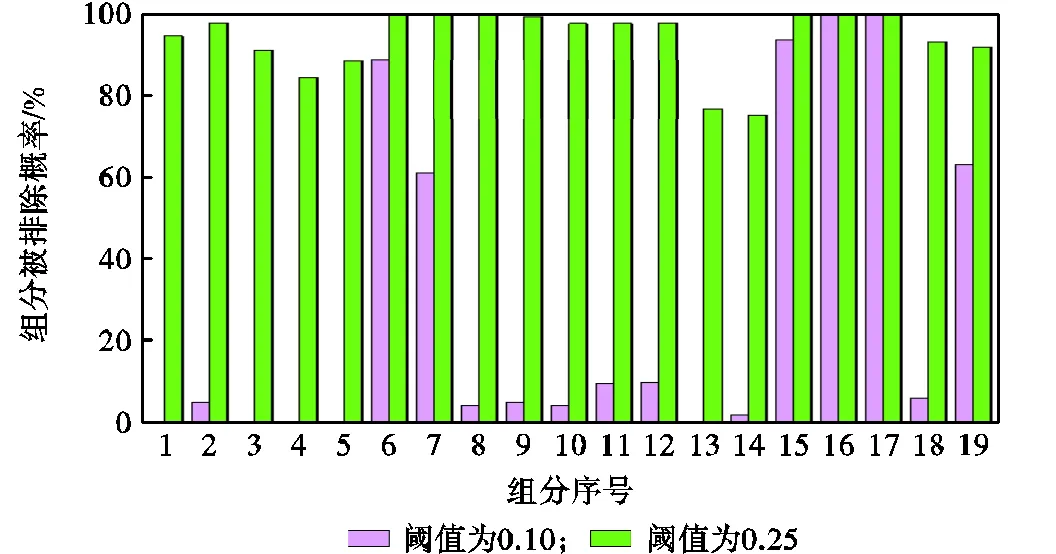
1—H2O2；2—C；3—CH；4—CH2；5—CH2(S)；6—CH3OH；7—C2H；8—C2H2；9—CH；10—C2H4；11—C2H5；12—C2H6；13—HCCO；14—CH2CO；15—HCCOH；16—C3H7；17—C3H8；18—CH2CHO；19—CH3CHO

从图2中可知，在阈值为0.1时，GDRG统计表明传统DRG方法排除的组分概率均达到60%以上，这与其他组分的排除概率形成鲜明对比．但在大阈值情况下，GDRG统计的被排除组分概率大小与DRG选择被排除组分并不一致，比如组分C在不确定分析下的排除概率接近100%，但DRG方法认为组分C是强耦合组分．为了表明组分C与模型的耦合性，在25组分的简化模型中删除C组分，其预测结果如图3所示．

从图3可知，相比于DRG方法得到24组分的简化机理，GDRG方法可得到预测能力更强的24组分的简化机理．这说明在大阈值下，首先DRG方法得到的简化机理是很不稳定的，容易出现非强耦合组分被强化的现象；其次，也说明在该大阈值情况下选择强耦合组分是非常困难的．了解传统DRG方法的局限性后，在选择排除组分时，把GDRG所统计出最高概率的12个非强耦合组分选择为排除对象，最终形成23个组分125个反应的简化机理．由于上述简化手段会删除很多组分，此时的机理很难有很强的预测能力，为了提高简化机理的实用性，本文应用最小二乘优化算法对简化机理进行优化．

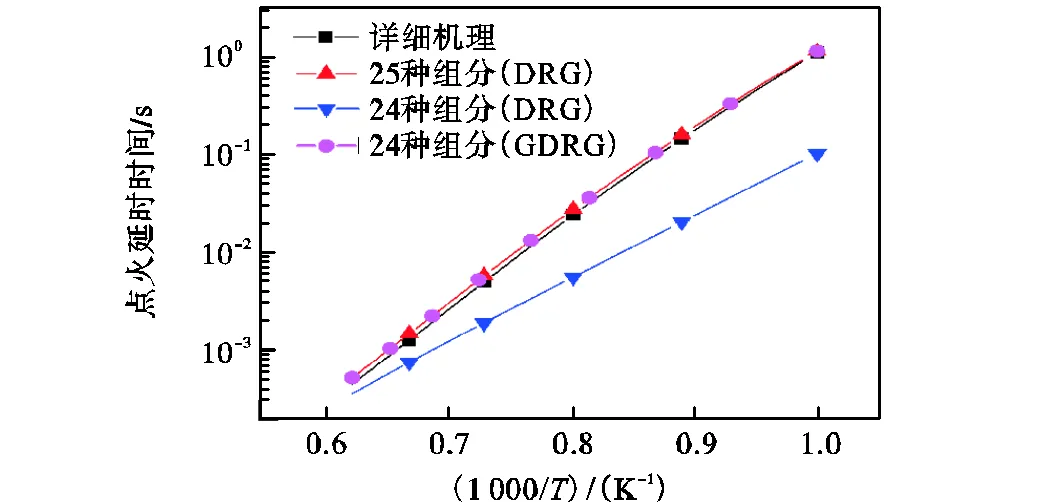
图3 比较不同简化机理和详细机理下所预测点火延时时间

2.2 骨架机理优化

在优化反应动力学机理之前，先运用FAST方法对简化机理进行全局敏感性分析，目的在于选择重要的基元反应供优化算法优化，由此降低优化参数的个数，缩减优化尺度和优化过程消耗的时间．全局敏感性分析简化机理模型各基元反应对点火延时的贡献如图4所示．从图中可以看出初始温度为1000K和1200K时，对点火延时时间起重要机理基本保持一致，但与初始温度在1400K和1600K时对点火延时起重要基元反应机理又相差很大．通过分析各初始条件下起重要的反应，考虑优化的目标数和优化能力，最终选择33个起重要作用的基元反应为优化对象.

图4 应用FAST方法分析简化模型所得到重要基元反应对点火延时时间的全局敏感性系数

当选择重要基元反应作为优化对象后，本文采用最小二乘法对33个反应机理进行优化，使简化机理预测结果向详细机理逼近，优化结果如图5所示．从图中可知，简化机理通过优化可以很明显提高机理的预测性能．此过程也验证了具有一定容差的简化机理可通过优化算法来弥补，也可以使简化手段发挥更加强大的作用．值得注意的是，如果拟合的目标为实验数据，会更加体现优化算法的性能．后续工作将继续开发此方法，使得优化的简化机理能进行更宽范围下的预测．

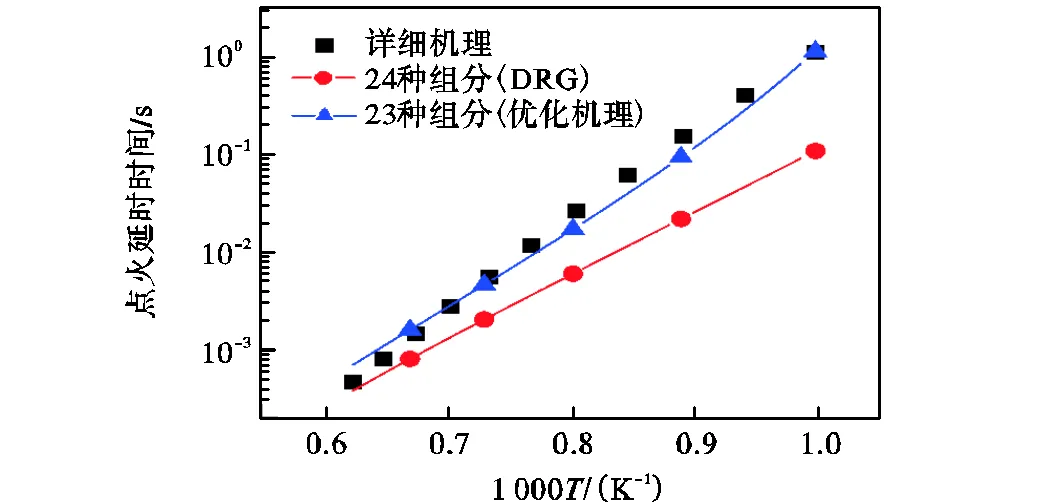
图5 比较简化机理和优化机理在点火延时时间上的预测能力

3 结 论

燃烧机理存在着很大的不确定性会导致传统简化手段所得到的简化机理也存在着很强的不确定性，大幅度反应动力学机理的削减容易导致强耦合组分被弱化或非强耦合组分被强化的现象．因此，本文基于不确定性分析方法讨论在机理速率不确定性下应用简化方法进行精简模型，并以DRG方法简化甲烷模型进行详细说明．为了在机理的不确定性下能应用DRG方法进行大幅度地削减反应动力学机理，并使得机理有很强的预测能力，首先运用概率的手段统计DRG方法所得到的非强耦合组分概率供简化模型准备，因为如果只应用传统方法简化会导致不重要的组分被强化；其次通过概率大小方式对燃烧机理进行有容差的简化，允许机理可以以一定误差的方式预测燃烧过程；最终通过全局敏感性方法辨别重要的机理，并应用优化算法对简化机理进行优化，弥补简化机理的预测能力．运用此系列方法最重要的目的在于简化手段可以有一定容差方法简化燃烧反应机理，以达到大幅度的削减模型的目的，为数值计算提供精简和预测性能强的简化机理．

［1］ Selle L，Lartigue G，Poinsot T，et al. Compressible large eddy simulation of turbulent combustion in complex geometry on unstructured meshes[J].，2004，137(4)：489-505.

［2］ Turányi T，Tomlin A S.[M]. Springer Berlin Heidelberg，2014：61-144.

［3］ Lu T，Law C K. A criterion based on computational singular perturbation for the identification of quasi steady state species：A reduced mechanism for methane oxidation with NO chemistry[J].，2008，154(4)：761-774.

［4］ Sun W，Chen Z，Gou X，et al. A path flux analysis method for the reduction of detailed chemical kinetic mechanisms[J].，2010，157(7)：1298-1307.

［5］ Gao X，Yang S，Sun W. A global pathway selection algorithm for the reduction of detailed chemical kinetic mechanisms[J].，2016，167：238-247.

［6］ Farrell N P C J T，Dryer F L，Friend D G，et al. Development of an experimental database and kinetic models for surrogate diesel fuels[C]//. 2007，2007-01-0201.

［7］ Elliott L，Ingham D B，Kyne A G，et al. Genetic algorithms for optimisation of chemical kinetics reaction mechanisms[J].，2004，30(3)：297-328.

［8］ Cukier R I，Fortuin C M，Shuler K E，et al. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory[J].，1973，59(8)：3873-3878.

［9］ Sobol I M. Sensitivity estimates for nonlinear mathematical models[J].，1993，1(4)：407-414.

［10］ Ziehn T，Tomlin A S. A global sensitivity study of sulfur chemistry in a premixed methane flame model using HDMR[J].，2008，40(11)：742-753.

［11］ Wang H，Sheen D A. Combustion kinetic model uncertainty quantification，propagation and minimization[J].，2014，47：1-31.

Global Reduction for Combustion Reaction Mechanism and Skeletal Mechanism Optimization

Lin Shengqiang1，Xie Ming1，Wang Jiaxing2，Zhou Weixing1，Yang Bin2

(1. School of Energy Science and Engineering，Harbin Institute of Technology，Harbin 150001，China；2. Center for Combustion Energy and Key Laboratory for Thermal Science and Power Engineering of MOE，Tsinghua University，Beijing 100084，China)

There exist uncertainties in the reaction rate coefficients of combustion mechanisms，which will affect the contribution of different reactions to the combustion characteristic parameters．Moreover，these uncertainties will also influence the statistics of contributions by different species in the reactions when the reduction method based on relation graph is employed，causing the coupling degree between species to be uncertain．In the present work，the combustion mechanism is simplified and optimized with the consideration of uncertainties in the reaction rate coefficients．First，1000 possible detailed mechanisms are obtained by uniform sampling in the uncertain parametric domain of rate coefficients．Then，the directed relation graph(DRG)method is applied to simplify these detailed mechanisms，and the removed species are counted and ranked．Finally，the model is reduced according to the probability．In addition，the global sensitivity analysis(GSA)method is applied to identify the key reaction in the skeletal mechanisms，and those with higher sensitivity are further optimized．In this way，the simplified mechanism with higher prediction accuracy can be obtained．

global sensitivity analysis(GSA)；directed relation graph(DRG)method；uncertainty analysis；least squares method

TK16

A

1006-8740(2019)05-0395-06

10.11715/rskxjs.R201901026

2019-01-26．

国家自然科学基金资助项目(91741204；91741109).

林圣强（1988—），男，博士，fujianlsq@163.com.

周伟星，女，博士，教授，zhouweixing@hit.edu.cn；杨 斌，男，博士，教授，byang@tsinghua.edu.cn．