基于WLLE和极坐标特征提取的叶片图像识别方法

丁 娇，张天飞，龙海燕，张 磊

(安徽信息工程学院 电气与电子工程学院，安徽 芜湖 241000)

0 引言

植物在人类生产和生活中都充当着必不可少的角色，是人类所依赖的生存基础条件.传统的叶片识别通过人工采集植物叶片，然后观测和测量植物的各种特征参数，从而判断叶片类别[1-5].该种方法不仅大量耗费人力物力和时间，且识别效率低.随着科学的不断进步，一些叶片智能识别系统应用而生[6-7]，这些系统结合了数据库技术以及模式识别技术，提高了叶片识别的准确率和识别时间.

传统的叶片识别系统在对从图像库中取出的叶片图像进行预处理后，大都是在直角坐标系下提取叶片的特征参数[8-9]，例如颜色矩特征提取、基于灰度共生矩阵的纹理特征提取等，它们利用的是图像像素点的底层特征.虽然计算简单，不具有易变性，但特征维数高，计算量大，而本文使用的特征参数是在极坐标下提取的，可缩短叶片特征提取的时间.

本文提出一种基于WLLE和极坐标特征提取的植物叶片识别方法，该方法首先对从图像库中选取的植物叶片图像进行预处理操作，然后将其从直角坐标变换到极坐标，提取高维极坐标特征参数，再利用降维算法WLLE对叶片高维极坐标特征进行维数约减，最后利用最近邻分类器实现叶片种类的识别.

1 叶片特征提取

1.1 图像预处理

首先从中科院合肥智能所建立的植物叶片数据库(http://www.intelengine.cn/data)[10]中选取实验所需要的叶片图像，该图像库中收纳了220种，共计16 846幅叶片图像.实验选取20幅金银花图像作为正类训练样本，再分别选取杜英、络石、含笑、夏枯草各20幅，共80幅图像作为负类训练样本.同时，从这5种植物叶片剩余的图像中各选取10幅，共50幅图像，作为实验的测试样本集.为了便于后期的分类实验，首先对从原图像库中选取的叶片图像进行大小处理，统一将实验图像调整为128*128[9]大小.

在对图像进行极坐标特征提取之前，需要对图像进行预处理操作，主要分为三步：1)彩色图像灰度化，目的是为了删去原始图像中的彩色信息；2)去噪：对图像进行滤波，去除噪声干扰[11-12]；3)图像二值化：突出图像中叶片有效区域，便于后期的叶片特征提取[13].

1.2 直角坐标到极坐标的变换

为了将图像从直角坐标(x,y)变换到极坐标(r,θ)，首先要计算得到二值化图像的质心[14]，计算公式为：

(1)

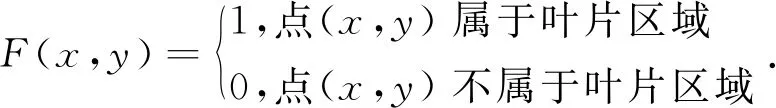
现选取二值图像的质心为直角坐标系的原点，则原直角坐标系下目标点(x,y)变换到极坐标下的坐标即为：

(2)

其中：r：直角坐标系中目标点(x,y)到质心的距离；θ：目标点与质心构成的向量(x,y)与向量(1,0)间夹角，且θ∈(0,2π).

1.3 叶片极坐标特征提取

将二值化图像从直角坐标转换到极坐标后，便可提取叶片图像的极坐标特征，所提取的特征参数包括：高度变化率、跨度比、圆饱和度和曲面面积比率，它们的计算公式分别为[14]：

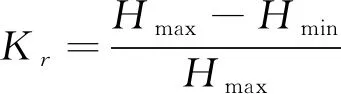
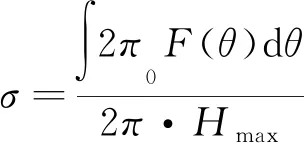
其中，Hmax：变换到极坐标下目标图像中的波峰；

Hmin：变换到极坐标下目标图像中的波谷；

S：波峰与波谷之间围成的面积；

SSum：目标图像整个矩形区域面积；

F(i):离散状态下，i角度在图像曲线中对应的高度值.

同时，这些极坐标特征经过证明，均具有旋转、缩放不变性[15].

2 加权局部线性嵌入算法(WLLE)

局部线性嵌入(LLE)[16]是一种最常用、最典型的流形学习算法，具有计算复杂度低、易于实现等优点，但是对高维样本降维的过程中极易受噪声的影响.为了改善这一缺陷，在LLE算法的代价函数中添加样本的重要性值，从而形成加权局部线性嵌入算法(WLLE).一般情况下，样本外点和样本噪声的重要性值均较小，因此，利用WLLE算法对高维样本进行降维的同时，能够有效抑制样本中噪声点和样本外点的干扰，降维效果较LLE算法好.

假设采样数据集X={x1,x2,…,xn}⊂RD，利用WLLE算法进行数据集X降维的具体过程[17]如下：

(a)对于数据集X中任一样本点xi，计算其与剩余所有样本点的欧式距离，并对欧式距离进行排序，找出与xi欧式距离较近的K个样本点，形成K邻域.K是预先给定的数值；

(b)对于数据集中每个样本点，利用其K邻域中各近邻点的线性组合来进行表示，并计算任一样本点xi与其近邻点xj的加权局部重构权值Wij.所计算的Wij应使式(3)的重构误差函数最小：

(3)

且Wij满足约束条件

(4)

(c) 根据式(5)计算样本点xi的重要性值Dii,

(5)

其中，

(6)

(d)计算原始数据集X的潜在低维流形Y，使得加权误差函数

(7)

最小，且低维流形Y应满足约束条件

(8)

(e)对对称矩阵M进行非稀疏对角化

M=D(I-W)T(I-W).

(9)

其中，D=[D11,D22,…,Dnn]，得到该矩阵较小的(d+1)个特征值及其对应的特征向量.由于第1个特征值几乎为0，因此低维流形Y即为第2～(d+1)个特征值对应的特征向量，d表示降维后空间的维数.

3 分类实验

本文通过四个实验来证明所提出方法的有效性，利用WLLE算法分别对从极坐标下提取的叶片特征、在直角坐标下提取的灰度统计特征和纹理边缘特征(面积凹凸度、矩形度、周长凹凸度、横纵轴比)进行降维，最后在低维空间利用最近邻分类器识别待测植物叶片图像.同时，本文还利用最近邻分类器直接对提取的多维极坐标特征进行分类，从而证明WLLE算法的有效聚类能力.

3.1 算法参数的选择

WLLE算法能够有效实现高维数据集的降维，同时也能够有效抑制样本中的噪声和样本外点，但是该算法包含了两个可调参数：近邻参数K和嵌入维数d，在算法运行的过程中，需要确定这两个参数的取值.通常选取的K值要比d值大，以此来提高算法的稳定性.根据实验所选取的训练样本的数目，同时便于低维空间中最近邻分类器识别待测样本，实验中K的取值确定为9，d的取值选为2.而算法中的β取经验值100[17].

3.2 实验结果

实验对从图像库中选取的正类、负类样本图像进行预处理后，将其全部从直角坐标系变换到极坐标系，在极坐标下每幅叶片图像提取的叶片特征参数构成一个4维的向量.利用WLLE分别对极坐标下提取的叶片特征、直角坐标下提取的灰度统计特征、纹理边缘特征进行降维，在低维空间利用最近邻分类器判别待测叶片图像的类别，每个实验重复10次，每次实验训练样本和测试样本在选定的植物叶片库中随机抽取，最终的分类结果取10次实验中最佳的分类率和平均分类率.表1所示为实验分类结果.

随机选取30幅叶片图像，将其在直角坐标下面积凹凸度、横纵轴比、矩形度、周长凹凸度4种特征提取时间与极坐标下曲面面积比率、高度变化率、跨度比、饱和度4种极坐标特征提取时间进行对比，对比结果如表2所示.由表2可知，极坐标特征提取时间较直角坐标特征短，因此，本文提取叶片极坐标特征可缩短叶片图像的分类时间.

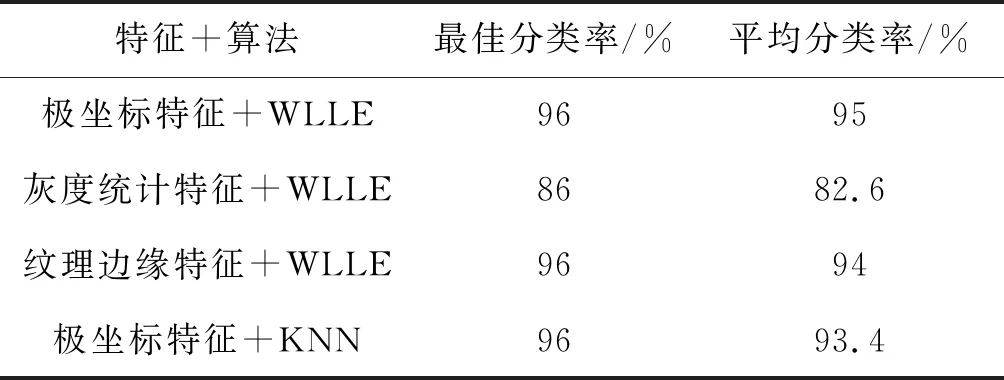
表1 叶片图像分类结果

表2 叶片特征提取时间对比

4 结束语

本文将维数约简算法WLLE与极坐标进行结合，提出一种新的植物叶片识别方法.首先将叶片图像从直角坐标系转换到极坐标系，在极坐标系下提取实验样本的特征参数；然后利用WLLE算法对叶片极坐标特征参数进行降维，实现叶片特征的有效聚类；最后利用最近邻分类器实现待测叶片图像的类别预测.由文中所给出的实验结果可知，本文所提方法不仅可以提高叶片图像的分类准确率，还能够有效缩短叶片的识别时间.