基于分类器学习算法的图像智能分类技术研究
吴海丽
(太原学院 计算机科学与工程系,山西 太原 030012)
0 引言
由于互联网多媒体和互联网等高科技的快速发展,以及近年来数字音频产品的出现,数字图像急剧增加[1].如何科学、高效、明智地管理这些海量数字图像并将其应用于社会生活的各个领域已经成为一个新的现代研究课题:如何正确地对这些科学图像进行分类?它已成为一个迫切需要社会解决的严重问题.过去,旧的图像分类方法通常是基于手工标注,但通常有两个难以解决的关键问题:首先,出于人为原因,人工标记的图像通常具有强烈的个人感觉,即主观性,第二,人工标记图像的数量相对较大,费力和耗时,并且其在大范围内的普及是困难的.基于内容的图像分类技术起源于20世纪80年代和90年代.该方法基本上使用了提取图像的基本特征,然后进行了一系列的操作和训练,最终达到了分类的目的.虽然基于分类器研究的图像分类方法现已获得一些重要的研究成果[2],但常用的方法是基于图像的特定特征,而图像中包括的内容普遍情况下是不仅仅一种,单一的某一特征并不能充分满足图像描述的需求,而基于分类器学习算法的图像智能分类技术因为其特别性能够最大化的处理这个问题.
伴随社会科学技术的发展和数码产品的大规模推广使用,图像已成为满足人们日常需求的必不可少的资源[3].根据相关社会调查的统计数据,人们大多使用视觉、听觉、嗅觉和触觉来获取有关环境的基本信息.通过视觉信息获得的信息约为60%,这也是人们所知道的.信息的关键.图像是视觉信息的重要来源之一:由于其内容丰富,存在形式丰富,叙事能力强,主题内涵深刻,远远超出了文本信息[4].图像描述的信息内容非常丰富,图像数量也呈指数快速增长,有明显的信息表明这种放大形式将持续很长时间.面对庞大的图像资源,实现完善,科学,有效管理,获取必要信息的方式已成为各界专业人士迫切需要的一个严峻的研究课题.图像分类是指自动完成给定图像集的智能分类或评估图像是否属于特定类别.今天,图像的具体描述基本上包括本世纪的两个非常复杂的问题.第一世纪的谜团指的是克服差距的语义边界的困难.国内外许多研究者对图像的主要特征进行了深刻的诠释,如颜色,形状,纹理和时空关系,并利用这些功能完成图像叙事.基于这些基本特征,计算机测量图像之间的相似性.然而,当人们测量图像相似度时,它们主要是基于对高级图像的语义边界的深刻理解,很难研究高级图像的基本特征和语义边界.复活节的巨大深渊.
第二个问题是图像受到许多因素的影响,例如亮度,移动幅度,大小和变形.识别标志的难度继续增加.同时,这些因素显着增加了解决差距语义边界的复杂性.在20世纪80年代早期,模式识别仅限于统计识别和结构模式识别[5]. 20世纪80年代末90年代初,快速发展的模糊数学逐渐渗透到模式识别中的一系列关系,出现了一种求解模糊模式识别的技术.这是因为不同实体的特征通常反映了事物的相反方面.通过匹配具有相同特征的不同分类器,它们可以在从不同角度收集结果时反映该特征.因此,对于不同的分类.组件的组合可能全面地反映相同的模式以实现最佳的分类结果,因此几个分类器的有机组合可以最大化整体接受度.
1 基于分类器学习算法的图像智能分类技术
图像智能分类重点需要解决三个重要性的问题:首先,应该怎样正确表示图像;其次,应该怎样正确标记样本;最后,应该怎样对小样本进行学习.为了解决以上这三大问题,本文提出了一种全新的分类器学习算法,称之为Classification learning algorithm算法[6].该算法以多样性密度算法探寻到的区域最大值MAX来建构出一个全新的属性空间,将线映射为属性空间中的具体某一点,最后通过分类器学习机(Classifier learning machine,CLM)技术在MIL 框架下对图像进行智能分类.
1.1 图像分割与特征提取
给定一幅具体的图像,采取分类器学习算法对其进行精准分割并提取到图像的具体特征.先把图像分割成大小一致的为3×3的无重叠图像小块,提取到每一个小块的颜色特征以及纹理、空间特征.其中:颜色特征表现为将小块由红黄绿的基准空间(RGB空间)转换为LPV空间( L表示颜色亮度,PV则表示图像色度) ,取LPV三个分量的平均值作为颜色特征,由此可获知三维立体颜色的特征向量[7].纹理特征则是采取Daubichy-3对3×3的图像小块进行次一级小波频率转换得到最少3个频率带,一个低频LP和三个高频LH,HL,HH,每一个频率带均包含2×2 个系数.不失普遍性,假设HH频率带的系数是{∂k,l,∂k,l+1,∂k+1,l,∂k+1,l+1},那么HH频率带的小波特征具体表示为:
(1)
LH,HL的小波特征具体可以参照HH 获取,由此能够求到三维立体纹理颜色特征向量.采用L-means 方法把分割以后的图像小块结合成若干个类,每一类对应图像的某一具体纹理颜色区域,那么区域Ri就可以表示为Δfi. 形状特征具体是指对图像的任何一个区域Ri,利用阶数为1,2,3的归一化惯性因子去叙述其具体的形状特征.惯性因子λ的公式表示见下式:
(2)
其中,Δr为区域Ri的中心质点;r为区域Ri中每一个像素的具体坐标;V为区域Ri的像素总和.在三维立体空间内,分割区域的最小外接圆的惯性因子最小,假设最小外接圆的第γ个惯性因子是Iλ,区域Ri的立体三维形状特征可根据下式计算获取:
(3)
如此一来,一幅图像就被分成n个区域的图像B,具体可以表示为:
(4)
对应着图像区域Ri的10维的特征向量.
1.2 关键点精确定位
由于DoG值对图像噪声和周围边缘敏感[8],因此有必要对在DoG标度空间中检测到的区域的极值点的函数进行三维立方比较,以便精确地确定关键点的位置和比例. 相应的图像边缘值不稳定的点和像素对比度相对低的点被去除,从而增加了特征点的稳定性和降低噪声水平的可能性.
(5)
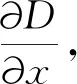
(6)
2 实验与效果分析
为了更加清楚、具体地看出次技术方法的实际应用效果,特与传统算法的图像智能分类技术进行对比,对其分类速度和精确度进行比较.
2.1 实验准备
为保证试验的准确性,将两种技术设计置于相同的试验参数之中,进行分类速度和精确度试验.实验采取的Corel-1K图像数据集,一共分成8组,分别为:African people,villages,Historical building,Dinosaurs,Elephants,Flowers,Mountains以及Food.每一组包含150副格式为JPEG的彩色图像,图片分辨率均设置为380×256或256×380.运用两种算法的图像分类技术对图像进行分类处理,提取底层特征形成包(图片)与示例(K域).最终的结果是,示例为一个10维的列向量三维LUP特征、3维纹理颜色特征以及3维形状特征,包为若干个示例组建的矩阵图.
2.2 实验结果与分析
为了测试基于分类器学习算法的智能图像分类技术的有效性,将其与经典算法DD-SVM和MILES进行了比较.在基于分类器学习算法的图像智能分类技术的实验中,为每种类型的图像随机选择100个图像并将其添加到训练集中,将剩余的50个图像作为测试样本添加到测试集中,并将20个图像标记添加到实验集中.正数,30未标记,在其他类别的图像中随机选择100个图像,其余50个图像被添加到测试集.在添加到实验组中的其他类图像中,20个是负的,30个不标记.每个实验重复5次,取平均精度.最终结果如图1所示.
基于分类器学习算法的智能图像分类技术可以充分利用被识别对象的各种特征空间,很好地结合分类器之间的信息互补性,有效地改善分类过程,但是分类器采用的组合结构另外,组合分类算法也不同用户很难理解他们的决策过程.提高组合分类的可理解性对其推广和应用具有一定的推动作用.
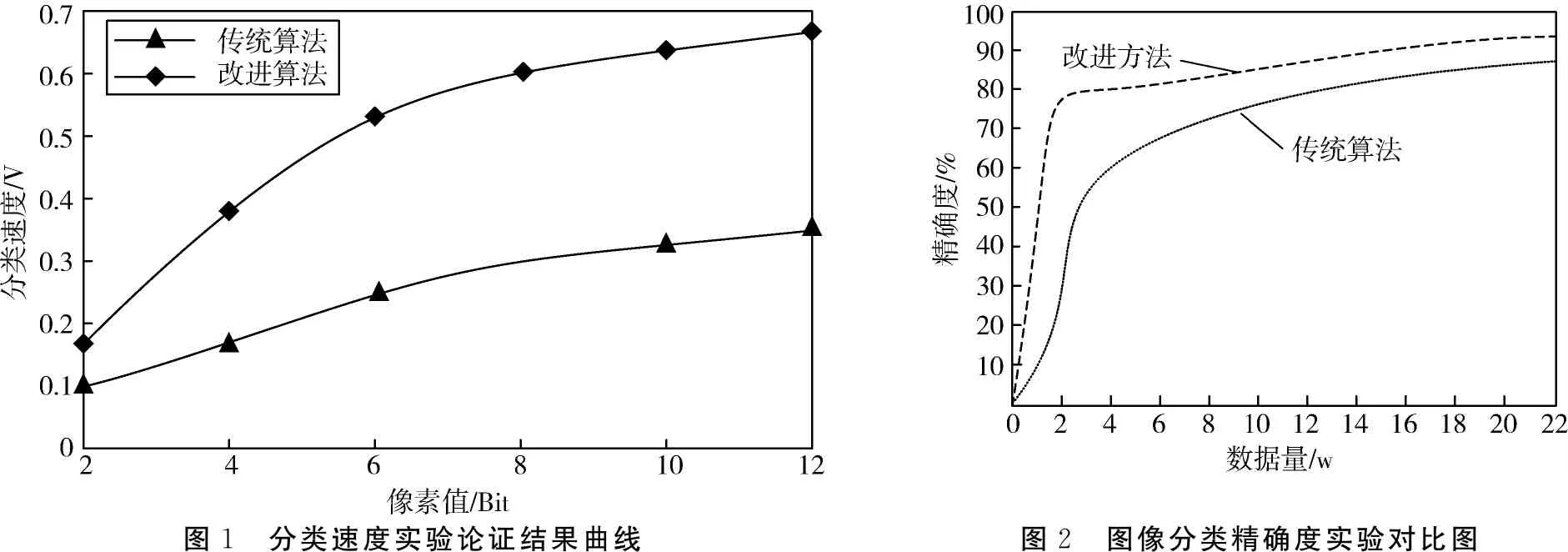
图1 分类速度实验论证结果曲线图2 图像分类精确度实验对比图
通过实验结果的显示,在分类速度上,两种算法下的图像分类速度差别较大,但是本文设计的基于分类器学习算法的图像智能分类技术在后续上比较具有优势.在图像精确度上,本文设计的基于分类器学习算法的图像智能分类技术相比于传统算法的分类技术,精确度要更高,且一直居高不下.
3 结束语
本文对基于分类器学习算法的图像智能分类技术进行分析,依托分类器学习算法与数学模型技术的双向结合,根据图像分类技术遇见的技术难题,对图像智能分类进行的调整,实现本文设计.实验论证表明,本文设计的方法具备极高的有效性.在今后的工作中,不断完善本论文的研究工作,包括进一步测试,分析和改进智能图像分类技术在实际应用中的性能,以实现更高性能的组合分类系统,继续研究分类器的组合,为深入研究图像分类奠定基础,为大规模且不断更新的数据分类问题做好最佳解决方案.希望本文的研究能够为基于分类器学习算法的图像智能分类技术的发展提供理论依据.

