基于胶凝原油可压缩性的含蜡原油管道停输再启动模型研究*
王健 杨天雪 翟宇佳 孙云鹏 陈夏欢
华北油田公司第四采油厂
含蜡原油含有大量的石蜡基质,当原油管道出现意外停输或计算停输工况时,随管道内部温度的降低石蜡会形成凝胶,从而在管道内部形成一段胶凝原油塞,可对管道的再启动过程造成严重的影响[1-4]。国内外诸多学者进行含蜡原油管道的停输再启动研究时,常将管道内的胶凝原油看作不可压缩流体[5-10],以简化停输再启动模型的建立和计算过程。然而,在实际过程中,由于胶凝原油可压缩性的影响,其屈服过程是一个渐变的过程,并且在屈服过程中存在较为明显的屈服面移动现象。因此将胶凝原油简单地视作一种不可压缩流体不能准确地描述含蜡原油管道的停输再启动过程。
因此,在考虑胶凝原油压缩性前提条件下,采用双流体驱替方程,建立基于胶凝原油压缩性的停输再启动模型,模拟胶状含蜡原油管道停输后的再启动过程,并通过对方程的求解,获得含蜡原油管道在停输再启动过程中的流动特性,对比不可压缩模型与可压缩模型的计算结果,得出了管道内部的流动规律,揭示了胶凝原油压缩性对停输再启动过程的影响规律。
1 停输再启动模型
1.1 模型假设
在进行停输再启动作业时,管道内原油的流变性和密度将随时间的变化而变化,同时注入流体可以是水或具有与胶凝原油相同性质的原油,但本文为更好地进行双流体驱替数学模型的建立以及简化模型求解和计算过程,做出以下假设:
(1)假设管道内的胶凝原油(OGF)的初始物理性质是均匀的(即原油的非均匀性是在管道重新启动后才产生的)。
(2)假设注入的流体(ICF)为与时间无关的宾汉流体。
(3)ICF和OGF之间的交界面平行于管径方向。
(4)当管道内壁面的剪切应力高于流体的静屈服应力时,凝胶结构开始破裂,同时流动开始,OGF被ICF所取代。
1.2 启动过程模拟
在实际进行停输再启动作业时,管道内胶凝原油的屈服过程是一个渐变的过程,如图1所示。当在管道入口处施加一定的压力时,管道入口处的一段原油(Lf)将会在应力的作用下发生屈服形变,如果应力大小超过胶凝油塞的静态屈服压力,已发生形变的胶凝原油将会在压力的驱动下向前移动。与此同时,ICF进入管道内部,当屈服前沿到达胶凝油塞的末端时(t =t0),整个胶凝油塞将同ICF以相同的速度一起运动。图2显示了整个过程中的压力变化过程。
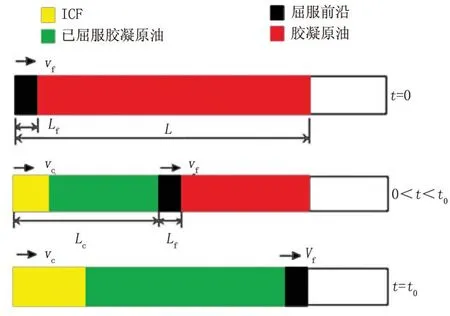
图1 管道内原油的屈服过程Fig.1 Yield process of crude oil in pipeline
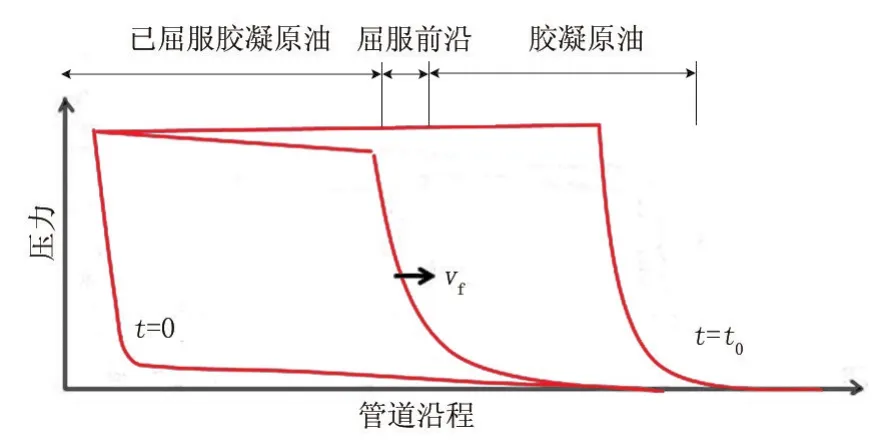
图2 管道沿程的压力变化过程Fig.2 Pressure change process along the pipeline
由图2可知,管道进行停输再启动作业时,管道内部压降的变化由两部分组成,即已屈服的压缩流体区域的压降和屈服前沿的压降。
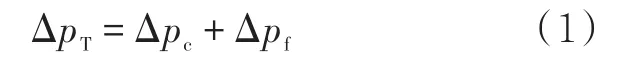
如果忽略流体在压力条件的物理性质变化,则其压降可用公式(2)计算。

式中:τc表示与压缩段流体流动有关的壁面剪切应力,Pa; D为管道内径,m; Lc为压缩段流体长度,m。
由于屈服前沿在压降的作用下会发生微小的扰动,因此其压降由两部分组成,即无黏流动压降和克服静态屈服应力所需压降。
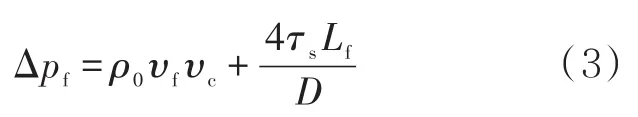
式中: ρ0为原油在大气压条件下的初始密度,kg/m3;υf为屈服前沿的移动速度,m/s; υc为ICF流体的流速,m/s; Lf为屈服前沿的长度,m;τs为静态屈服压力,Pa。
由于受胶凝原油压缩性的影响,导致在压力条件下其密度会发生改变,其密度和压力之间的关系式为

式中: β为压缩因子,为常数; p为压力,Pa。
当屈服前沿的长度Lf足够小,并且入口压力足够大时,屈服前沿穿过胶凝原油的速度近似于声速,因此屈服前沿的移动速度可以用公式(5)计算。
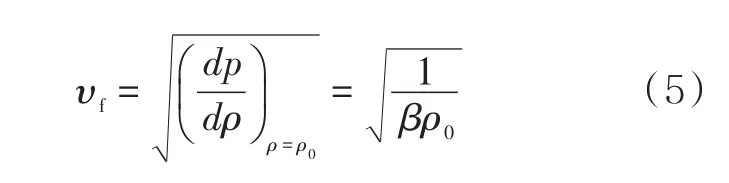
由此得到屈服前沿通过胶凝原油塞长度L所需的时间为

式中:L为胶凝油塞的长度,m。
1.3 剪切时间模型
如果施加的入口压力足够大,使胶凝原油塞在t0时发生整体移动。为确定原油受到剪切应力作用时的变化情况,将t=0时的胶凝油塞划分为长度为ΔL0的M段(Δ L0=L/M ) ,且段长足够短。因此在各段内原油可视为不可压缩的,在各段内具有均匀的性质。
在t=0时,每一段将具有相同的性质,但随着时间的推移,在压力和胶凝原油可压缩性的作用下,每一段的长度和所经历的剪切时间会发生明显变化,每一段的长度变化过程如图3所示。

图3 每段长度随时间的变化过程Fig.3 Changing process of each segment over time
当t=t0时,胶凝原油的每一段经历了不同的剪切时间,剪切时间的长短取决于它的位置,每段剪切时间随管长的变化过程如图4所示,OGF流体中第k段所经历的剪切时间为

式中:M为胶凝油塞的段数。
当t≥t0时,当屈服前沿通过胶凝原油塞后,ICF和OGF会以相同的流速一起流动,OGF流体中第k段所经历的剪切时间为


图4 每段剪切时间随管长的变化过程Fig.4 Shearing time of each segment changing over the pipeline length
1.4 压缩位移模型
随时间的推移,OGF不断地被清除出管道,与此同时ICF进入管道内,在时间t(t ≥t0)时,管道内的ICF段长度为

式中:ΔLk,OGK表示第k段胶凝原油的长度,m;m为停留在管道中的OGF段数;K为在t=t0时管道中ICF流体的段数。
在时间t(t ≥t0)时,管道内的OGF段长度可由公式(10)计算。

式中:ΔL0为胶凝原油分段的初始长度,m;ΔLk,OGK为第k段胶凝原油的长度,m;Δpk表示第k段压降,Pa;
将管道内部的动量方程简化为准稳态条件下的力学平衡式(壁面切应力和管道内压降之间的平衡),因此在任一段中的壁面剪切应力计算公式为

式中:ΔLk表示第k段长度,m。
1.5 OGF和ICF的流变模型
胶凝原油的流变学特性是以北海含蜡原油[11]为基础建立的,屈服应力和时间的关系为
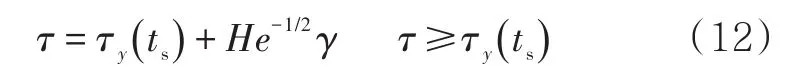
其中,

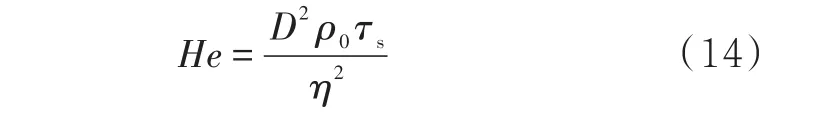
填入的ICF流体为与时间无关的宾汉流体,剪切应力关系式为

式中:τB为宾汉流体屈服应力,Pa; HeB为宾汉流体的海兹特鲁姆数,无量纲。
1.6 摩擦系数模型
将公式(11)中剪切应力的表达式用流速表示,可以转化为
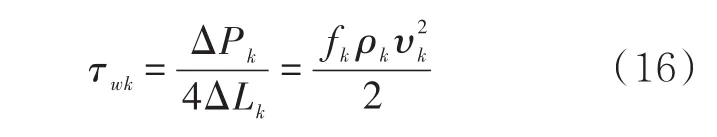
式中: fk为摩擦因数; ρk为第k段的密度,kg/m3;υk为第k段的速度,m/s。
当流动是层流时,ICF的摩擦因数可以用公式(17)计算。
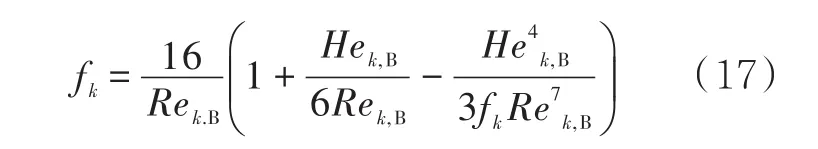
其中,
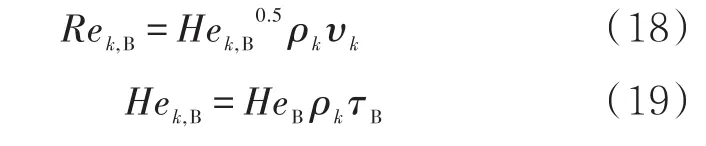
式中:Hek,B为第k段宾汉流体的海兹特鲁姆数,无量纲;Rek,B为第k段宾汉流体的雷诺数,无量纲。
OGF的摩擦系数可以用公式(20)计算。
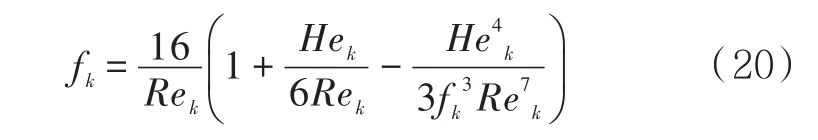
其中,

式中: Hek为第k段的海兹特鲁姆数,无量纲;Rek第k段的雷诺数,无量纲。
随管道重启过程的不断进行,管道内流量不断增加,原油的表观黏度随流量的增加呈逐渐降低的趋势,因此,若施加的压力足够大,管道内的流动状态将会从层流变为湍流。
对于湍流,ICF流体和OGF流体的表达式相同,DARBY等[12]在分析HANKS等人的文献[13]基础上,建立了摩擦因数的经验表达式
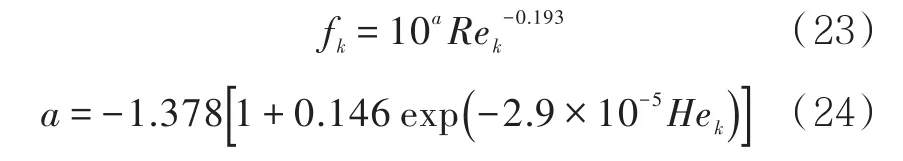
为了方便模型的建立和求解,使用了由DARBY[12]提出的摩擦因数的统一表达式

式中: fkL为层流摩擦因数,由公式(17)~公式(22)计算得出; fkT为湍流摩擦因数,由公式(23)~公式(24)计算得出。
2 结果与讨论
为了验证本文所建立的含蜡原油停输再启动模型的准确性,采用与CNR模型[9]相同的计算参数进行计算验证与对比,其中OGF为来自北海的含蜡原油,其流变性可用公式(12)~公式(14)来表示。相应的参数取值为:0.172, λ=0.004 06, He=5.16×105,同时假定ICF是一种与时间无关的宾汉流体τB()∞=0.172,He=5.16×105;大气压下的ICF/OGF密度比为1,并假定管道内全部为胶凝原油填充,环境温度为-18℃,压缩系数 β=3.606×10-6。为了作图的方便性,对结论图标的坐标轴进行无量纲处理,其中 :,与CNR模型相同,本文计算的管道沿长L/D=32787。
2.1 可压缩模型与不可压缩模型的对比分析
图5为在相同压降条件下(ΔpT/τs=1.375×10-5),建立的模型与CNR模型的计算结果对比,其中,纵坐标为质量流量G/(ρ0D2vref)、横坐标为时间t/tref,均为无量纲(下同)。从图中可以发现CNR模型在施加压差后立即开始流动,并且流型由层流向湍流的过渡十分突然[14]。而当考虑了胶凝原油的压缩系数之后,管道内胶凝原油的流动发生在一定压差之后,并且较好地实现了流型变化的平稳过渡。若将本文所建立的模型的压缩性值取为0,则计算结果与CNR模型相一致。当 β=3.606×10-6时,管道完成重启需要的质量流量比CNR模型高17.6%。
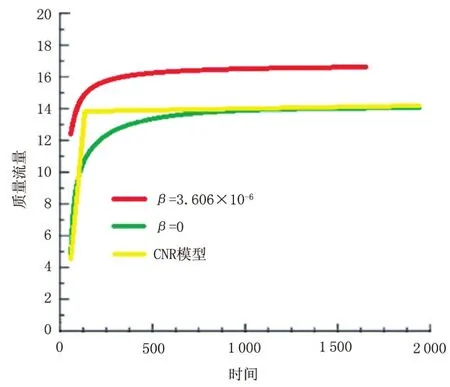
图5 不同模型间的质量流量计算结果对比Fig.5 Comparison of mass flow calculation results among different models
图6为在相同压降条件下(ΔpT/τs=1.375×10-5),ICF与OGF交界面距离入口处的距离随时间的变化关系,其中,纵坐标为交界面距离入口处的距离LICF/D,横坐标为时间t/tref,均为无量纲。从图中可以发现当假设胶凝原油为不可压缩时(CNR模型和 β=0),施加压力后,胶凝原油塞立即开始移动,但对于考虑了胶凝油塞压缩性的模型( β=3.606×10-6),只有施加压差一定时间后才开始移动[15-16],开始移动的时间即为屈服前沿到达管道末端所需的时间t0。

图6 交界面距离入口处的距离随时间的变化关系Fig.6 Distance from the interface to the entrance changing over time
2.2 不同压缩性的影响分析
图7为不同胶凝原油压缩系数条件下质量流量的模拟计算结果,当 β=0时,由于原油密度不受压力的影响,因此不存在因压缩性引起的位移。

图7 不同压缩性条件下的质量流量计算结果对比Fig.7 Comparison of mass flow calculation results under different compressibility conditions
当 β 由3.606×10-7提高到3.606×10-6时,最终质量流量增加11%,整个重启动作业时间减少12%。随着压缩性的增加,再启动的时间减少。
2.3 管道内部压力分布规律分析
图8为在相同压降条件下(ΔpT/τs=1.375×10-5),启动3个不同时间节点后管道沿线的压力分布。其中,纵坐标为交界面距离入口处的压力 p/τs、横坐标为管道沿程L/D,均无量纲。从图中可以发现,在ICF区域压力分布的斜率随着时间的增加而逐渐增大,而在OGF区域,由于随时间变化的屈服应力衰减,压力分布的斜率随着时间的增加而逐渐减小[17-19]。

图8 不同时间点管道沿线的压力分布Fig.9 Pressure distribution along the pipeline at different time points
3 结论
(1)本文建立的含蜡原油管道停输再启动的双流体驱替模型合理考虑了胶凝原油的可压缩性因素,相较之不可压缩模型能更准确地预测含蜡原油管道的停输再启动过程。
(2)胶凝原油的可压缩性对管道停输再启动过程的影响作用不可忽略。当 β=3.606×10-6时,管道完成重启需要的质量流量比CNR模型高17.6%,管道完成重启所需的时间缩短了12%。
(3)在ICF区域,管道内压力分布的斜率随着时间的增加而逐渐增大,而在OGF区域,由于随时间变化的屈服应力衰减,压力分布的斜率随着时间的增加而逐渐减小。

