基于LSTM循环神经网络的核电设备状态预测
龚 安,马光明,郭文婷,陈 臣
(中国石油大学(华东) 计算机与通信工程学院,山东 青岛 266580)
0 引 言
随着中国经济的迅速发展,核电站的发展规模日益扩大[1],为保证对核电系统安全状态的及时掌控,核电设备运行状态的预测变得越来越重要。然而,基于核电数据的保密性等原因,通过核电数据对核电设备运行状态进行预测,还未发现相关的研究,因此研究核电设备运行状态的预测方法很有意义。
核电系统属于复杂结构系统,结构越复杂,系统数据的复杂性越大。普通的预测方法如灰色预测模型[2]、比例风险模型[3]、非线性滤波器模型[4]都局限于因果回归,并不能有效反映时序数据和设备运行状态之间的关系。
近年来,深度学习模型在时序数据的研究越来越深入[5],其中LSTM神经网络[6]通过设备产生的时序数据预测其运行状态已经取得了不少成功的案例。例如,Noriaki Hirose等提出基于LSTM的滚动摩擦预测模型[7],对机械系统的滚动摩擦进行研究,实验结果精确预测了设备的滚动摩擦系数;Chen Zaifa等将LSTM模型和经验模式分解算法相结合,用LSTM模型处理轴承数据的本征模函数分量,并将实验结果与支持向量机相对比,更好地实现了机械状态的单步预测[8];AbdElRahman ElSaid等使用LSTM模型实现了飞机发动机振动值的预测[9],并由此建立了飞机发动机状态预警系统,避免了过渡振动对飞机的不利影响;Zhao Rui等使用LSTM获取磨损数据的依赖关系,提出基于LSTM评估的生活工具健康检测系统[10],并通过对比实验展示了LSTM模型的优越性。
在上述研究的基础上,文中采用LSTM神经网络对核电设备运行状态进行预测,选择某核电站数据中的主泵绕组温度作为实验数据进行对比实验,包括数据预处理、网络结构设计、神经网络的训练和预测等算法的实现。实验结果表明该方法对核电设备运行状态有更高的预测精度。
1 相关理论
1.1 数据预处理
数据预处理是数据挖掘的重要步骤,同时也是必不可少的一环。为了更有效地挖掘出知识,必须为数据挖掘模型提供简洁、干净、有效的数据。然而,实际应用系统中获得的原始数据通常含有脏数据,存在杂乱性、重复性、不完整性等方面的问题。
通过数据预处理对应的模块,以领域知识作为指导,对原始数据进行处理,摈弃与数据挖掘目标无关的属性,为数据挖掘的核心算法模型提供更准确和更有针对性的数据,以提高数据挖掘的效率和准确度。
数据预处理相关理论与方法很多,然而,对于复杂设备时序数据的预处理,目前还没有相关理论方法的深入研究。为了提高实验精度,除了手动除去噪点之外,实验采用z-score标准化方法对实验数据进行预处理,其公式可表示为:
z=(x-μ)/σ
(1)
x为具体的实验数值;μ为平均数;σ为标准差。
1.2 LSTM神经网络的相关理论
循环神经网络在网络结构设计中引入时序数据的概念,使其在时序数据处理中具有更强的适应性。RNN (recurrent neural network)虽然能够有效处理时间序列数据,但仍存在以下两个问题:(1)RNN存在梯度消失和梯度爆炸问题,无法有效处理时间维度过长的时间序列数据;(2)RNN模型的训练过程中需要预先设定延迟窗口的长度,但是这一参数的最优值难以获取。
LSTM神经网络是众多RNN的变体之一,在普通RNN的基础上,在各隐藏层神经单元中加入记忆单元,实现时间序列上的记忆信息可控。每次序列数据在隐藏层各单元之间传递时会通过遗忘门、输入门、输出门等可控门,控制时序数据中之前数据和当前数据的记忆和遗忘程度,从而使神经网络具有长期记忆功能。通过这种方式,LSTM神经网络有效改善了循环神经网络梯度消失、长期记忆力不足等缺点[11-12],能够有效地利用长距离的时序数据。

图1 RNN隐藏层细胞结构
ht=f(Wxhxt+Whhht-1+bh)
(2)
yt=Whyht+by
(3)
其中,W表示权重系数矩阵;b表示偏置向量;f表示激活函数。
LSTM神经网络的神经元细胞结构如图2所示[13],计算公式可表示为:

图2 LSTM隐藏层细胞结构
it=σ(Wxixt+Whiht-1+Wcict-1+bi)
(4)
ft=σ(Wxfxt+Whfht-1+Wcfct-1+bf)
(5)
ct=ftct-1+ittanh(Wxcxt+Whcht-1+bc)
(6)
ot=σ(Wxoxt+Whoht-1+Wcoct+bo)
(7)
ht=ottanh(ct)
(8)
其中,i,f,c,o分别表示输入门、遗忘门、细胞状态、输出门;W和b分别对应权重系数矩阵和偏执系数;σ和tanh分别对应sigmod和双曲正切激活函数。
训练过程可分为四个步骤:
(1)由式4~式8计算LSTM细胞的输出值;
(2)计算每个LSTM细胞的误差;
(3)根据误差计算每个权重的梯度;
(4)应用基于梯度的优化算法更新权重。
LSTM有许多变体,最成功的是门限循环单元(gated recurrent unit,GRU)。GRU模型保留了LSTM的长期记忆能力,将LSTM细胞中的输入门、遗忘门、输出门替换为更新门和重置门,并将细胞状态和输出两个向量合二为一。GRU结构相对简单,参数数量少,训练效率较高,在实际应用中,两者的可比性很强。
1.3 梯度下降算法
梯度下降算法是机器学习领域使用最广泛的优化算法,在许多流行的深度学习库中都包含了不同版本的梯度下降算法的实现。基于梯度下降的优化算法有多种,比如Adam[14-15]、AdaGrad[16]、RMSProp[17]等。文中选用随机梯度下降算法(stochastic gradient descent,SGD)[18]。SGD算法的优化过程为:在给定的样本M中,随机取出副本N代替原始样本M来作为全集,对模型进行训练。这种训练方式优势明显,如果样本抽取在合适范围内,既会求出结果,并且速度更快。
SGD算法能够有效解决训练过程随实验样本数量加大而变得异常缓慢的问题,有效提高收敛速度并减少占用的设备资源。
2 构建LSTM神经网络的预测模型
根据设备运行数据的特点,结合第一节提到的相关理论,给出基于LSTM模型的核电设备运行状态预测方法,包括模型的搭建、训练和预测。
2.1 预测模型框架的搭建
考虑到实验数据是单变量时间序列数据,构建的LSTM神经网络预测模型如图3所示。该模型由五个功能模块组成,包括输入层、隐藏层、输出层、网络训练和网络数据预测。输入层对实验数据集进行初步处理:划分数据集,数据标准化,数据分割等以满足LSTM神经网络的输入要求;隐藏层用LSTM细胞搭建循环神经网络:遗忘门决定保留多少上一时刻的神经元状态到当前时刻神经元状态,输入门决定保留多少当前时刻的输入到当前时刻的神经元状态,输出门决定当前时刻的神经元状态输出的多少;输出层提供预测结果。网络训练使用SGD算法更新权重,在保证精度的前提下提高了优化效率。网络数据预测使用迭代的方法进行数据预测。

图3 LSTM模型框架
2.2 LSTM模型的训练和预测
首先,定义原始的设备状态时间序列数据为:
f={f1,f2,…,fn}
(9)
为了适应隐藏层输入的特点,应用数据分割方法对数据集f进行处理。设定分割窗口长度(数据步长)为L,分割后的数据集为:
F={F0,F1,…,Fn}
(10)
Fp={fp*L+1,fp*L+2,…,fp*L+L},0≤p≤t
(11)
然后,将实验划分为训练集train_x,train_y和测试集test_x,test_y两部分。
训练集可表示为:
Ftrain_x={fp*L+1,fp*L+2,…,fp*L+m}
(12)
Ftrain_y={fp*L+m+1,fp*L+m+2,…,fp*L+L},1 (13) 测试集可表示为: (14) (15) train_y,test_y分别为train_x,test_x的理论输出。 接下来将训练集train-x,train-y输入到隐藏层训练神经网络。实验设定训练集与测试集的大小比值为9∶1,则模型隐藏层输出C和train-y均为(0.9*t,L-m)的二维数组。选择均方误差作为误差计算公式,训练过程的损失函数可表示为: (16) 把损失函数最小化作为实验的优化目标,选择不同的学习率和训练步长,应用SGD优化算法不断更新权重,得到最终的预测模型。 应用训练好的LSTM模型进行预测,将测试集test_x输入到模型,利用测试集test_y作为理论输出和模型的实际输出来计算模型的预测精度。 本节使用核电数据作为实验数据集,应用第一节的相关理论和第二节的模型构建方法展开实验验证,具体包括数据准备、实验结果、对比实验分析三部分。 实验采用主泵绕组温度作为实验对象。主泵绕组温度是反映核电设备运行状态的重要参数,主泵绕组温度的高低决定着核电设备实时的运行状态。数据时间范围:从2010年1月17日13点56分到2017年02月16日15点0分,数据量:采样频率为1分钟1条数据,总数据量为3 725 343。 部分时间序列数据如图4所示。 图4 主泵电机绕组温度 误差度量方式的选择对模型误差的计算有很大影响。常见的误差度量方式有:均方误差(mean squared error,MSE),计算参数估计值与参数真值之差平方的期望值;均方根误差(root mean squared error,RMSE),计算均方误差的算术平方根;平均绝对误差(mean absolute error,MAE),计算绝对误差的平均值。对于预测模型精度的计算,通常选择平均绝对误差作为度量标准。MAE的计算公式可表示为: (17) 其中,ft和yt分别为设备运行状态时间序列数据在t时刻的实际值和模型的输出值;T为数据点个数。通过对测试集计算MAE值来评估模型的预测精度。 实验所使用的计算机配置如下:处理器为(英特尔)Intel(R) Core(TM) i7-4720HQ CPU @ 2.60 GHz(2601 MHz);内存为8.00 GB;操作系统为Ubuntu 16.04;程序设计语言为Python3.5.2;集成开发环境为PyCharm Community Edition 2016.3;实验程序中所用到的RNN,LSTM和GRU模型由Python的TensorFlow程序包实现。 3.4.1 获取精度较高的模型参数 根据经验确定模型参数。分别选用5、10、15和20作为数据步长,选用不同的学习率(η=0.001,0.002,0.005,0.01,0.02,0.05,0.1)来训练LSTM模型。通过测试数据来检验模型精度,实验结果如表1所示。 表1 不同参数下LSTM模型的MAE 由表1可看出,当数据步长为15、学习率η=0.02时,LSTM模型的预测精度最高,MAE为0.030 5。 3.4.2 LSTM模型与RNN模型和GRU模型的对比 为了验证LSTM模型在不同类型的循环神经网络中的优势,实验中改变模型的隐藏层神经单元,构建RNN和GRU网络模型,并采用相同的多组参数对RNN模型和GRU模型进行训练,得到预测精度最高的RNN模型和GRU模型。实验结果表明,RNN模型预测精度最高时MAE=0.034 5,GRU模型预测精度最高时MAE=0.032 6。 LSTM与RNN对比结果如图5所示。 LSTM与GRU对比结果如图6所示。 实验结果表明,LSTM模型的预测精度明显高于RNN模型,略高于GRU模型。 文中深入探究了设备状态预测的主要方法,针对所获得的核电数据的特点和核电设备运行状态预测的需求,提出了基于LSTM神经网络的核电设备运行状态预测方法。对比实验结果表明:基于LSTM模型的预测方法与RNN模型和GRU模型相比,有更高的预测精度;LSTM模型在训练过程中模型精度对学习率的取值较为敏感,过高和过低都会影响模型的预测性能;与其他循环神经网络(RNN和GRU)相比,LSTM的预测精度更高,但训练过程耗时更多。 图5 LSTM与RNN对比结果 图6 LSTM与GRU对比结果 总的来说,验证了LSTM模型在核电数据分析领域的适用性,扩展了深度学习的应用范畴。基于当前的工作,后续将从以下方面继续研究:扩展隐藏层的数目,检验多隐藏层的实验结果;寻找有效的参数优化方法,提高参数优化效率和预测精度。3 实验验证
3.1 实验数据集
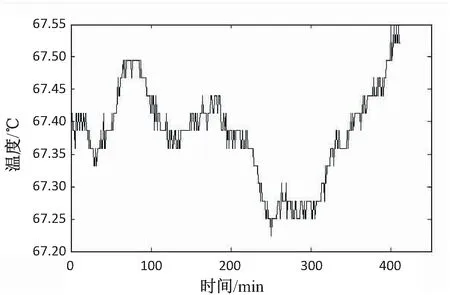
3.2 度量指标
3.3 实验平台和环境
3.4 实验结果

4 结束语



