基于SolTrace的线性菲涅尔式聚光器建模与仿真

马 军，王成龙，夏养君

(1.兰州交通大学 国家绿色镀膜技术与装备工程技术研究中心，甘肃 兰州 730070；2.兰州交通大学 光电技术与智能控制教育部重点实验室，甘肃 兰州 730070)

引言

太阳能作为一种理想的可再生能源已备受关注，但是能流密度低，提高利用效率的关键是先聚光再利用[1]。根据聚光形式，太阳能聚光系统主要有槽式、线性菲涅尔式、塔式和碟式等[2-5]。线性菲涅尔式聚光器主要由反射镜场、接收器、太阳跟踪控制装置三部分构成，具有结构简单、风阻小、成本低、土地利用率高等优点，正逐渐在大规模电站中得到应用[6-8]。

Sharma V等[9]推导出了线性菲涅尔式聚光器在任意时刻的余弦效率、末端损失效率和阴影与遮挡效率的表达式。杜春旭等[10]通过矢量分析，给出了线性菲涅尔式聚光器东西场和南北场镜场末端损失、大气衰减、余弦系数等光学效率。赵金龙等[11]利用光线追迹的方法建立了线性菲涅尔式聚光器的三维光学几何模型并给出其光斑能流密度分布的计算式。上述研究主要针对聚光器反射镜场的效率，对于光斑能流密度是基于接受器为平面进行分析的。但是线性菲涅尔式聚光太阳热能高温高压系统需要复合抛物面聚光器(CPC)和真空集热管构成的接收器[6]，分析真空集热管表面能流密度分布对传热效率分析至关重要。

本文利用几何光学原理推导了线性菲涅尔式聚光器在SolTrace软件中建模所需参数的计算公式，利用Matlab软件编程计算并建模。对集热管表面能流密度分布进行了分析，并给出了优化设计的建议，对线性菲涅尔式聚光器的推广应用具有指导意义。

1 线性菲涅尔式聚光器模型

线性菲涅尔式聚光器的接收器放置在距反射镜所在平面的高H处，第n列反射镜(平面镜)与水平面的夹角为βn(倾斜角)，其中心与镜场中心的距离为Qn。由文献[12]可知Qn和任意时刻的βn可计算求得。线性菲涅尔式聚光器的布置原理如图1所示。

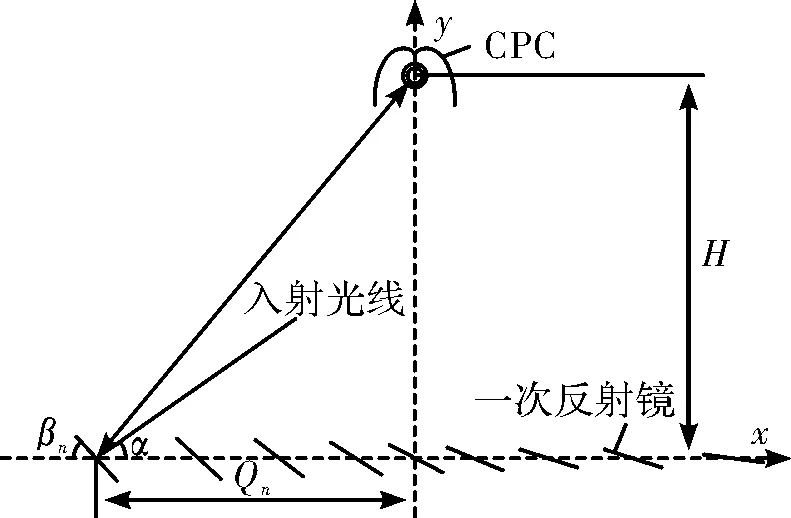
图1 线性菲涅尔式聚光器原理图

1.1 反射镜场模型

线性菲涅尔式聚光器的反射镜从西向东依次编号为1至N，第n列反射镜在SolTrace软件中的坐标参数可由几何关系得：

(1)

Y_Coordn=Z_Coordn=0

(2)

令Z_AimPtn=1，则

(3)

Y_AimPtn=0

(4)

“孔径”选择“矩形”,“表面”选择“平面”。

1.2 接收器模型

线性菲涅尔式聚光太阳热能高温高压系统需要复合抛物面聚光器(CPC)和真空集热管构成的接收器。

1.2.1 CPC模型

CPC剖面轮廓曲线主要有两种形式，分别为渐开线+抛物线和渐开线+cusp reflector曲线[13]。前者的单边是抛物线的一段，因此有焦点；后者是由Winston提出，Ortabasi等[14]推导出方程式并称为cusp reflector曲线方程，该曲线没有焦点。两种形式的CPC都关于中心轴对称，因此对其建模只需考虑截面的某一侧即可，本文建立左侧的CPC模型。CPC开口到真空集热管圆心的间距为d。

1) 基于SolTrace软件的渐开线部分坐标参数

X_Coordinv=Y_Coordinv=0

(5)

Z_Coordinv=H-d

(6)

此时

X_AimPtinv=Y_AimPtinv=0

(7)

Z_AimPtinv=Z_Coordinv+1

(8)

“孔径”选择“单轴式曲率部件”,“表面”选择“旋转对称三次样条”，数据格式为

(9)

其中:N是点数，(x1，y1)是渐开线与抛物线的切点坐标;(xN，yN)是渐开线坐标方程导数为零的点坐标。

求得CPC左半段渐开线的单调递增部分，对于单调递减部分，可由与其关于y轴对称的单调递增部分旋转求得，数据格式与(9)式相同。

2) 基于SolTrace软件的曲线部分坐标参数

CPC曲线部分若为cusp reflector曲线，则

X_Coordcus=Y_Coordcus=0

(10)

Z_Coordcus=H-d

(11)

此时

X_AimPtcus=Y_AimPtcus=0

(12)

Z_AimPtcus=Z_Coordcus+1

(13)

“孔径”和“表面”选择与渐开线部分相同。

CPC曲线部分若为抛物线，则

X_Coordpara=Δx

(14)

Y_Coordpara=0

(15)

Z_Coordpara=H-Δy

(16)

此时

X_AimPtpara=1+Δx

(17)

Y_AimPtpara=0

(18)

(19)

式中:θc为CPC最大接受半角;Δx和Δy分别为CPC抛物线在x轴和y轴方向的移动量。

“孔径”选择“单轴式曲率部件”，“表面”选择“抛物线”。

1.2.2 真空集热管模型

基于SolTrace软件的真空集热管坐标参数如下：

X_Coordtub=Y_Coordtub=0

(20)

Z_Coordtub=H-r

(21)

此时

X_AimPttub=Y_AimPttub=0

(22)

Z_AimPttub=Z_Coordtub+1

(23)

“孔径”选择“单轴式曲率部件”，“表面”选择“圆柱”。

2 算例分析

本文算例采用文献[12]中线性菲涅尔式聚光器镜场参数，反射镜列数为21列、宽度为0.38 m、长度为4 m，CPC最大接受半角为45°，接收器距反射镜所在平面5.3 m(集热管圆心与反射镜所在平面的距离)。CPC分别选用渐开线+抛物线和渐开线+cusp reflector曲线两种类型。利用Matlab软件编程计算用于SolTrace软件的线性菲涅尔式聚光器光学几何参数并建模。CPC为渐开线+cusp reflector，太阳垂直照射时线性菲涅尔式聚光器光路如图2所示。

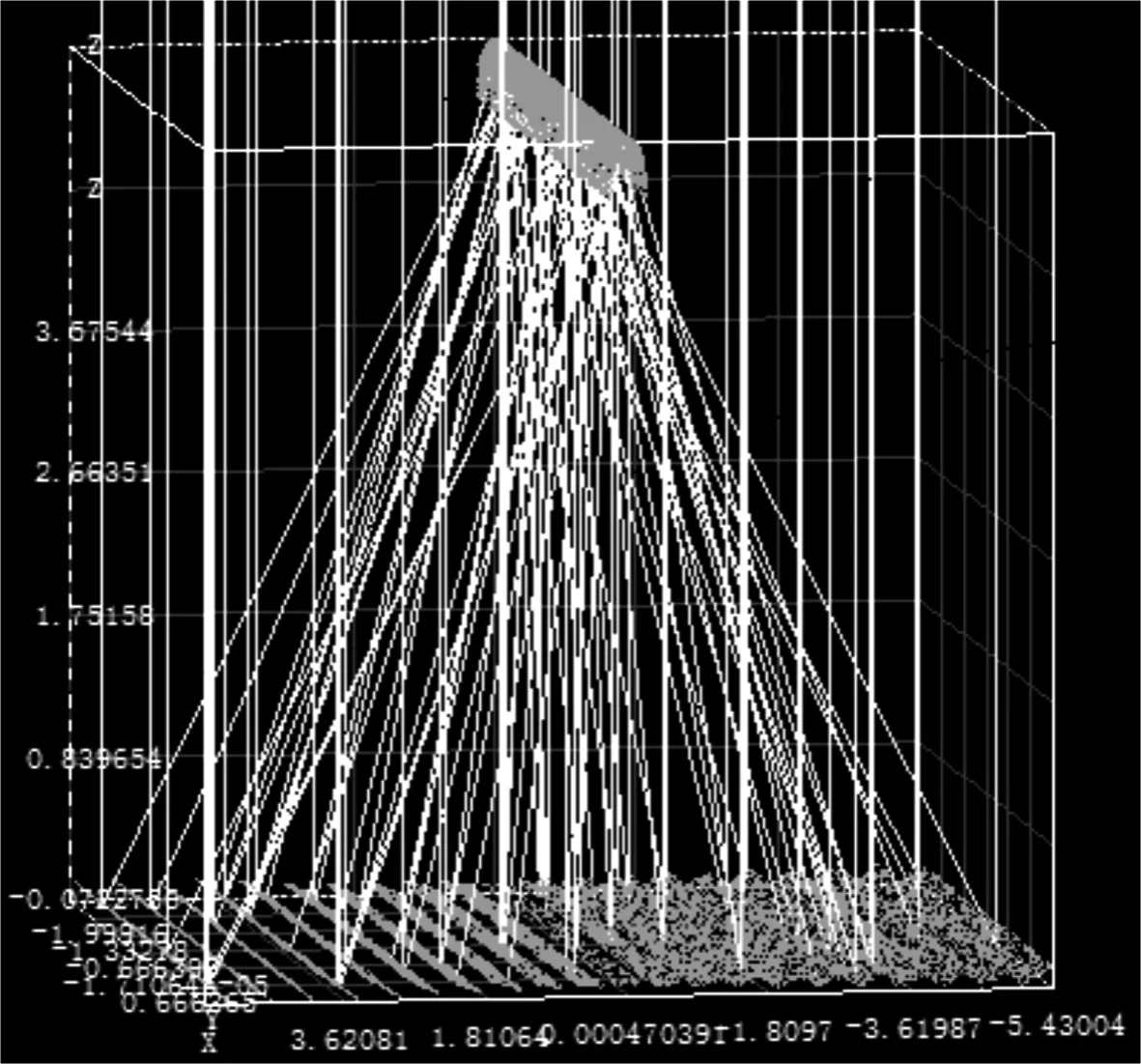
图2 太阳垂直照射时线性菲涅尔式聚光器光路图

在直射辐照度(DNI)为1 000 W/m2的条件下，CPC分别为渐开线+抛物线和渐开线+cusp reflector曲线的集热管表面的能流密度分布如图3所示。

图3 集热管表面的能流密度分布

能流均匀度定义为能流标准差与均值的比值。集热管表面能流密度和能流均匀度随太阳入射角度的变化情况分别如图4和图5所示。

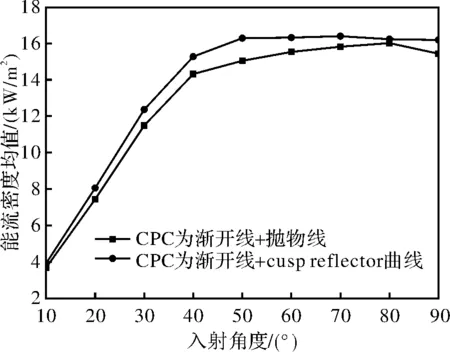
图4 集热管表面能流密度

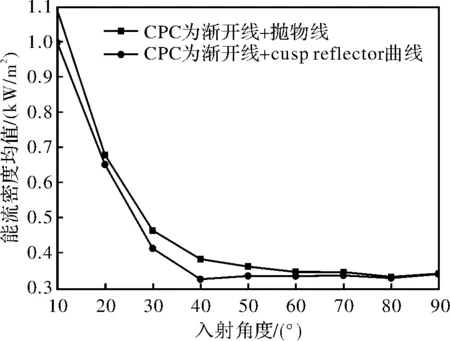
图5 集热管表面能流密度均匀度

由图4和图5可知，随着太阳入射角度的增大，集热管表面能流密度逐渐增大且分布更均匀；当太阳入射角大于40°后，能流密度和能流均匀度趋于稳定；CPC为渐开线+cusp reflector曲线比渐开线+抛物线的集热管表面能流密度更大且分布更均匀。

CPC为渐开线+cusp reflector曲线，当太阳入射角由10°增大到90°时，集热管表面能流密度从3.92 kW/m2增大至16.18 kW/m2。当太阳入射角为20°时，集热管表面能流密度为8.06 kW/m2；当太阳入射角为60°时，集热管表面能流密度为16.31 kW/m2。太阳入射角为40°～90°的集热管表面能流密度的平均值为16.11 kW/m2，聚光器光学效率为57.05%。

文献[12]选择聚光器无阴影工作时间为6 h，即太阳入射角度大于45°后工作，本文仿真结果与其吻合。

3 结论

本文建立了基于SolTrace软件的线性菲涅尔式聚光器的模型。仿真结果表明，对于反射镜列数为21列、宽度为0.38 m、长度为4 m，CPC最大接受半角为45°，接收器距反射镜所在平面5.3 m的线性菲涅式聚光器，随着太阳入射角度的增大，集热管表面能流密度逐渐增大且分布更均匀；当太阳入射角大于40°后，能流密度均值和均匀度趋于稳定；CPC为渐开线+cusp reflector曲线比渐开线+抛物线的集热管表面能流密度更大且分布更均匀。