结合神经网络和Q（λ）-learning 的路径规划方法

王 健，张平陆，赵忠英，程晓鹏

（1.沈阳新松机器人自动化股份有限公司 特种机器人BG，沈阳110169；2.沈阳科技学院 机械与交通工程系，沈阳110167）

路径规划是移动机器人的一项重要功能，用于引导移动机器人在地图中自主运动。 路径规划的优劣直接影响移动机器人的运动效率、机器损耗和工作效率。 与其它机器学习方法不同，增强学习方法无需监督信号，而是通过智能体与环境之间的信息交互进行“试错”，以极大化评价反馈信号为目标，通过学习得到最优或次优的搜索策略。 总体来说，增强学习的主要目标就是将状态映射到动作的同时，最大化期望回报。

随着增强学习理论和算法的不断发展与成熟，应用增强学习方法解决移动机器人路径规划问题正成为路径规划的研究热点[1]。 文献[2]提出了改进的Q-learning 方法用于解决单个机器人的路径规划问题， 通过引入标志位减少了学习过程的收敛时间，提高了算法的效率；文献[3]提出用神经网络模型来解决最短路径规划问题；文献[4]提出基于分层强化学习的路径规划方法；文献[5]对基于神经网络和POS 的机器人路径规划方法做了较为深入的研究。 强化学习是目前机器学习中富有挑战性和广泛应用前景的研究领域之一[6]。

目前，传统的强化学习方法在移动机器人路径规划应用中，由于其学习初始阶段对环境没有先验知识，往往存在收敛速度慢、学习时间长等问题。 故在此通过引入神经网络方法， 对传统Q-learning 算法进行改进，优化设计奖励函数，提出了基于神经网络的改进Q-learning 学习算法。

1 Q（λ）-learning 算法

Q-learning 是一种与模型无关的强化学习方法，在环境未知条件下，通过不断试错和探索，对所有可能的状态和动作进行多次尝试，采用数值迭代方法逼近最优解。

它以状态-动作对应的Q（s，a）为估计函数，逐渐减小相邻状态间Q 值估计的差异达到收敛条件，即

式中：S 为状态集；A 为动作集；T（s，a，a′）为状态s下执行动作a 后转换到状态s′的概率；R（s，a）为状态s 下执行动作a 的奖励；γ 为折扣因子。 寻找最优Q 值Q*（s，a）的搜索策略为

更新公式为

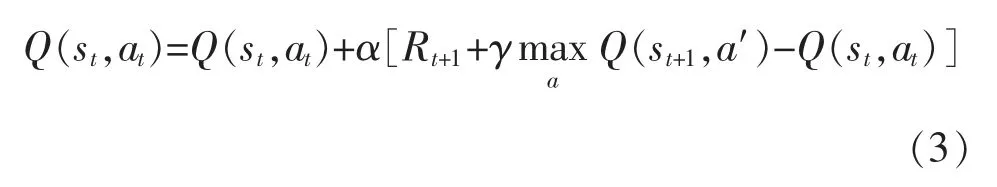
在Q-learning 算法中引入迹的思想， 能够记录状态被访问的次数，在更新前一时刻的状态值函数时， 也能对之前的状态值函数进行更新， 即Q（λ）-learning 算法。 其更新公式为

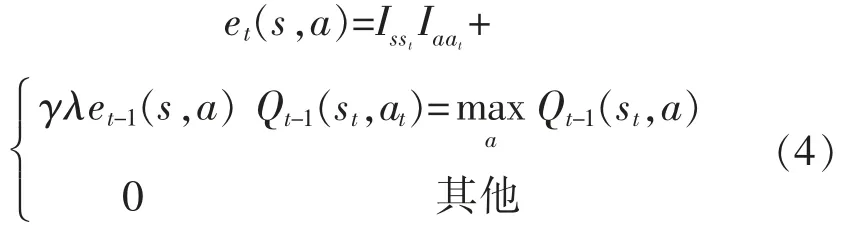
式中：Isst和Iaat为指数函数，如果s=st则值为1，反之为0。 误差项为

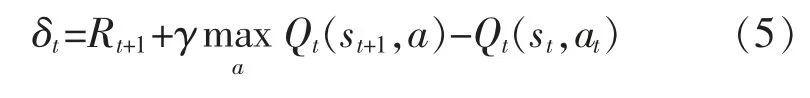
更新动作公式为

搜索函数为

式中：σ 为0～1 之间的随机数；ε 为探索因子，为0～1 之间的数。

2 受生物启发的神经网络方法

受生物神经系统中Hodgkin 和Huxley 细胞膜模型[7]与Grossberg 分流细胞模型[8]的启发，文献[9]提出了受生物启发的神经网络方法，用于解决移动机器人路径规划问题。 该神经网络方法状态方程为

其中

式中：xi为第i 个神经元的神经活动 （神经元细胞膜的电势）；A，B，D 分别为被动衰减率、神经活动的上限和下限， 均为非负常数；和[Ii]-为第i 个神经元的刺激性、抑制性输入；Ii为第i 个神经元内部输入；E 为正整数，且E＞＞B；[]-，[]+分别为取正、取负函数。该取正、取负函数的功能为

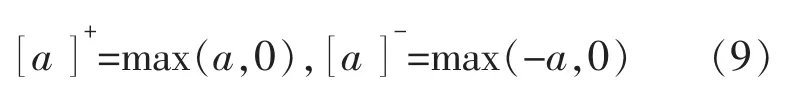
状态方程（8）中，第i 个神经元与第j 个神经元之间的权值连接ωij为一个距离函数。 其表达式为

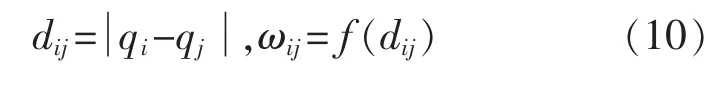
其中

式中：dij为状态qi和qj之间的欧氏距离；μ 和r0为正整数。

该神经网络方法不需要学习过程，根据神经元细胞之间的信息传递，可以求出神经元细胞所在状态的势值函数。 通过实时更新势值函数，移动机器人从初始位置沿着势值增大的方向到达目标位置，从而得到规划路径。

3 结合神经网络和Q（λ）-learning 算法

3.1 优化设计奖励函数

在Q-learning 算法中，奖励R（s，a）表示状态s下执行动作a 得到的奖励。 奖励值的大小直接影响动作选择的正确性和误差传递的效率。 因此，奖励函数设计的好坏，直接影响算法的收敛速度和最优解的质量。

传统的Q-learning 算法， 一般将目标状态的奖励设为很大的正整数，障碍物状态设为很小的负整数，其余状态处的回报值均为0。这种方式的奖励函数没有启发性，机器人在初期学习阶段很难到达目标，导致收敛速度很慢。

在此，奖励函数的设计采用文献[9]所提神经网络方法。 令状态方程（8）中，A=10，B=D=1，E=100，μ=1，r0=2，则状态方程转化为

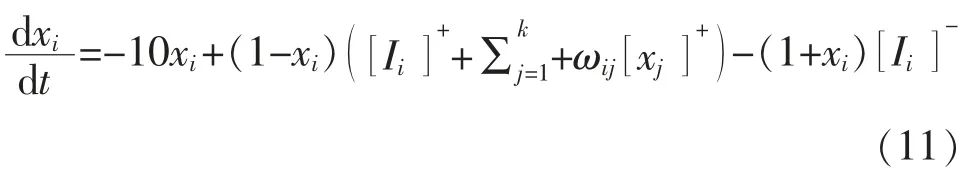
该神经网络模型可以确保从目标状态发出的刺激性信息，通过神经元之间的横向连接，传递给该工作空间的所有状态，而从障碍物传出的抑制性信息只在有限的范围内传播。

通过状态方程（11）可以得到每个状态势值，势值矩阵为X。 将奖励函数定义为

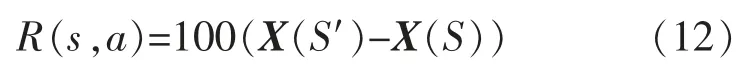
式中：X（S′）为执行下一个动作的状态势值；X（S）为当前状态势值。

3.2 算法实现流程

结合神经网络和Q（λ）-learning 算法，具体的实现步骤如下：

步骤1利用状态方程（11），经过k 次迭代，求出状态势值矩阵；

步骤2根据式（12），计算出奖励函数R（s，a）；

步骤3进行第i 次迭代计算， 最大迭代次数为n；

步骤4生成随机数σ，执行式（7）搜索策略π（s）；

步骤5执行动作a，得到奖励R（s，a），转移到新状态s′；

步骤6判断s′是否为终止状态， 如果是则跳到步骤3 进行下一次迭代（i=i+1），不是则跳到步骤7；

步骤7根据式（5），计算误差；

步骤8根据式（4），更新动作状态迹，并更新其他动作状态迹；

步骤9根据式（6），更新动作值函数；

步骤10s←s′，跳到步骤3，搜索下一个状态。

算法完成一次训练的流程如图1 所示。 该算法在迭代学习之前对根据环境地图信息进行状态势值计算，获得先验知识，以指导奖励函数设计，从而提高算法的收敛速度和最优解的质量。

4 仿真试验与结果分析

通过仿真试验来验证改进方法的有效性，试验环境采用20×20 栅格地图（如图2 所示），以图中左上角S 为移动机器人的起点， 以右下角E 为目标。图中， 白色部分为移动机器人的自由运动区间；黑色部分为障碍物，移动机器人无法穿越该区域。

图1 结合神经网络和Q（λ）-learning 算法流程Fig.1 Algorithm based on neural network and Q（λ）-learning flow chart

图2 最优策略示意图Fig.2 Optimal strategy schematic diagram

移动机器人动作集A 包括上移、右上、右移、右下、下移、左下、左移、左上等8 个动作；状态集包括400 个位置，障碍物和目标状态为终止状态。当移动机器人移动到终止状态， 则本次训练循环结束，重新进行下一次训练。

采用神经网络方法经过1000 次迭代计算得到的势值分布如图3 所示。 根据式（12）处理状态势值可以得到奖励函数R（s，a）。

图3 状态势值分布Fig.3 State potential value distribution

算法中几个重要的参数会直接影响收敛速度。仿真试验中，折扣因子γ 初始化为0.8，学习速率α初始化为0.05，探索因子ε 初始化为0.5，最大探索步数初始化为400。当搜索步数超过最大步数时，仍未到达终止状态，则认为此次训练失败，重新进入下一次训练。

采用经典Q-learning 方法， 在训练32000 次时收敛， 而本文方法仅需15000 次训练达到收敛状态，可见收敛速度有很大的提升。 训练完成的最优策略如图2 所示， 从起点到终点的最优路径如图4所示。

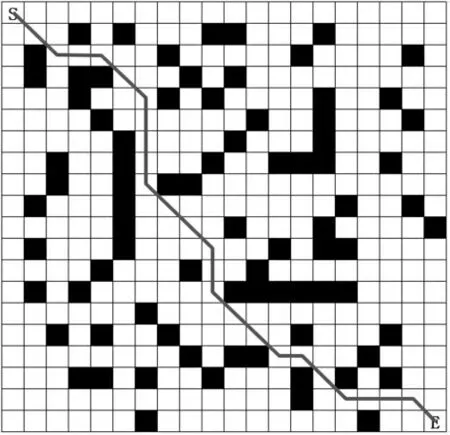
图4 从起点到终点最优路径Fig.4 Optimal path from start to end

采用同样的方法，生成另外3 个障碍物分布不同的栅格地图，使用同样参数完成训练。 统计移动机器人在地图所有状态下到达目标状态的平均步数，见表1。

表1 两种方法平均步数的对比Tab.1 Comparison of average steps between the two methods

移动机器人在所有状态移动到终点的平均步数越少，说明策略越优。 由表可知，本文方法在5 次试验中，平均次数均明显低于经典Q-learning 方法。

5 结语

所提出的结合神经网络和Q（λ）-learning 算法的移动机器人路径规划算法，通过优化设计奖励函数，为增强学习提供了先验知识，解决了强化学习中存在的收敛速度慢和解的局部最优问题。通过仿真试验，本文方法与经典学习方法相比较，验证了该方法的有效性。