基于混合算法的涡轴发动机稳态性能仿真模型

滕怀亮，李本威，钱仁军，董 庆

（海军航空大学，山东烟台264001）

建立发动机稳态性能仿真模型是航空发动机性能分析、故障诊断和控制系统设计等技术的前提，对于涡喷、涡扇发动机，已有大量文献对其性能仿真模型进行了研究[1]，但在结构和使用上，自由涡轮式发动机与涡喷、涡扇发动机存在较大差异[2]，自由涡轮直接连接输出轴带动直升机旋翼工作，所以对于选取共同工作方程和确定稳定状态参数的问题，涡轴发动机具有自身特点[3-4]。求解发动机模型本质上属于隐式非线性方程组的求解问题，发动机模型的非线性复杂度较高导致模型求解困难，将共同工作方程组的残差转化目标函数值，就将发动机模型的求解问题转换为最优化问题，而求解最优化问题的算法分为基于迭代的经典优化算法和基于随机搜索的现代智能优化算法[5]。

部分学者[5-7]使用N+1 点残量法、Newton-Raphson 算法或Broyden 秩1 法等经典算法对发动机模型进行求解，但经典算法对模型初猜值的准确度有较高要求，在设计点某些参数的值不完全明确的情况下，初猜值不准确会导致计算中断；而以粒子群算法[8-9]为代表的基于随机搜索的智能算法[10-13]，对初始解具有很好的包容性，只要初猜值没有超过热力计算时部件特性的范围，则模型一般不会出现计算中断导致的不收敛情况，可以得到一个较为合理的近似解，但智能算法求解得到的近似解往往比通过经典算法求解得到的解的精度低，且计算耗时较长。所以，部分学者研究了经典算法与智能算法结合的混合算法，骆广琦[14]等研究了PSO-N+1 点残量法的混合算法，王军[15]等研究了PSO-NR 融合算法，但粒子群算法计算耗时较长，要达到理想精度，对最大迭代次数和种群数量都有一定要求，须对算法参数进行精细调整。2017 年，Jiang[16]等考虑天牛使用2 个触须搜索的气味源的行为模式，将气味浓度与目标函数关联起来从而得到了新的优化算法——天牛须算法（BAS）。相比于粒子群算法需要大量粒子进行随机搜索，天牛须搜索只需要一只天牛个体，运算量大大降低。所以，为解决发动机模型非线性复杂度高，快速精确求解较为困难的问题，研究一种能够快速高精度收敛的混合求解算法，成为求解发动机模型的重要问题。本文建立了某型涡轴发动机稳态仿真模型，并提出了一种基于天牛须算法和N+1点残量法的混合求解算法。

1 气动热力仿真计算

根据该型自由涡轮式涡轴发动机的气路结构，定义发动机各计算截面，按顺序依次建立各计算截面之间的气动热力关系，分析梳理气动热力仿真计算过程。

1.1 发动机截面定义

根据该型自由涡轮式涡轴发动机的气路结构，定义发动机截面如图1所示，图1中各截面含义如表1所示。

图1 涡轴发动机截面示意图Fig.1 Sectional view of the turboshaft engine

表1 截面编号及含义Tab.1 Section number and meaning

1.2 稳态模型建立过程

涡轴发动机部件级模型的建立思路如下。

1）确定建模对象。即摸清发动机结构，定义各部件截面。本文建立的涡轴发动机模型由进气道、压气机、燃烧室、燃气涡轮、自由涡轮和尾喷管组成，如图1所示。

2）获取数据及数据预处理。获取包括各部件的特性数据、发动机设计数据、控制规律等。其中，压气机、燃气涡轮和自由涡轮的特性线尤为重要；在计算压气机、燃气涡轮、自由涡轮的流量和效率时需要对已知的部件特性曲面进行二维插值，为减小误差、提高模型的收敛性能，需要对特性线数据进行预处理[5，17]。

3）建立各部件的计算模型。根据各部件的气动热力学特征，采用变比热法建立各部件进出口参数的相关方程，完成从进气道进口到尾喷管出口的一次完整热力计算[17-18]。在建立各部件模型时，需要描述气体的压缩和膨胀过程，可以采用定比热或变比热法的2种方式进行计算。实际流动过程中气体比热容cp会随着压力和温度的改变而改变，因为发动机内部温度和压力变化较大，所以采用变比热法可以更精确地计算各截面参数。根据焓、熵、比热容和温度之间的经验公式建立气体流动过程中进出口参数之间的关系。

4）建立共同工作方程。根据完成一次热力计算所需的未知参数和控制规律建立发动机共同工作方程[6]。本文选取发动机台架试车数据验证模型，只计算空慢以上稳定状态，根据该型涡轴发动机的控制规律（自由涡轮转速不变），减少了一个未知参数，即减少了一个共同工作方程——自由涡轮和旋翼的功率平衡，降低了模型的非线性复杂度，提高了收敛性。

选定压气机增压比πc、燃气涡轮前温度T*4、燃气涡轮落压比πgt和自由涡轮落压比πft这4个未知参数为模型的待解参数，确定4个共同工作方程：燃气涡轮和压气机功率平衡，燃气涡轮进口流量平衡，自由涡轮进口流量平衡，尾喷管出口压力平衡。其方程为：

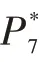
5）发动机稳态模型的求解。选定稳定工作状态（一般通过燃气涡轮转速或燃油流量确定），对未知参数试给初猜值，然后完成一次热力计算，通过共同工作方程检验试给的初猜值是否满足该稳定状态下的共同工作条件，当试给参数不符合共同工作方程的误差需求时，采用求解算法对初猜值进行更新，使其靠近各未知参数的真实解，进而使得残差方程组的误差满足精度要求[17-18]。

发动机模型的主要参数传递及迭代更新初猜值的过程如图2 所示，图2 中：Ma 为马赫数，H 为飞行高度，Wc为压气机流量。采用不同的求解方法即采用不同的初猜值更新方法。

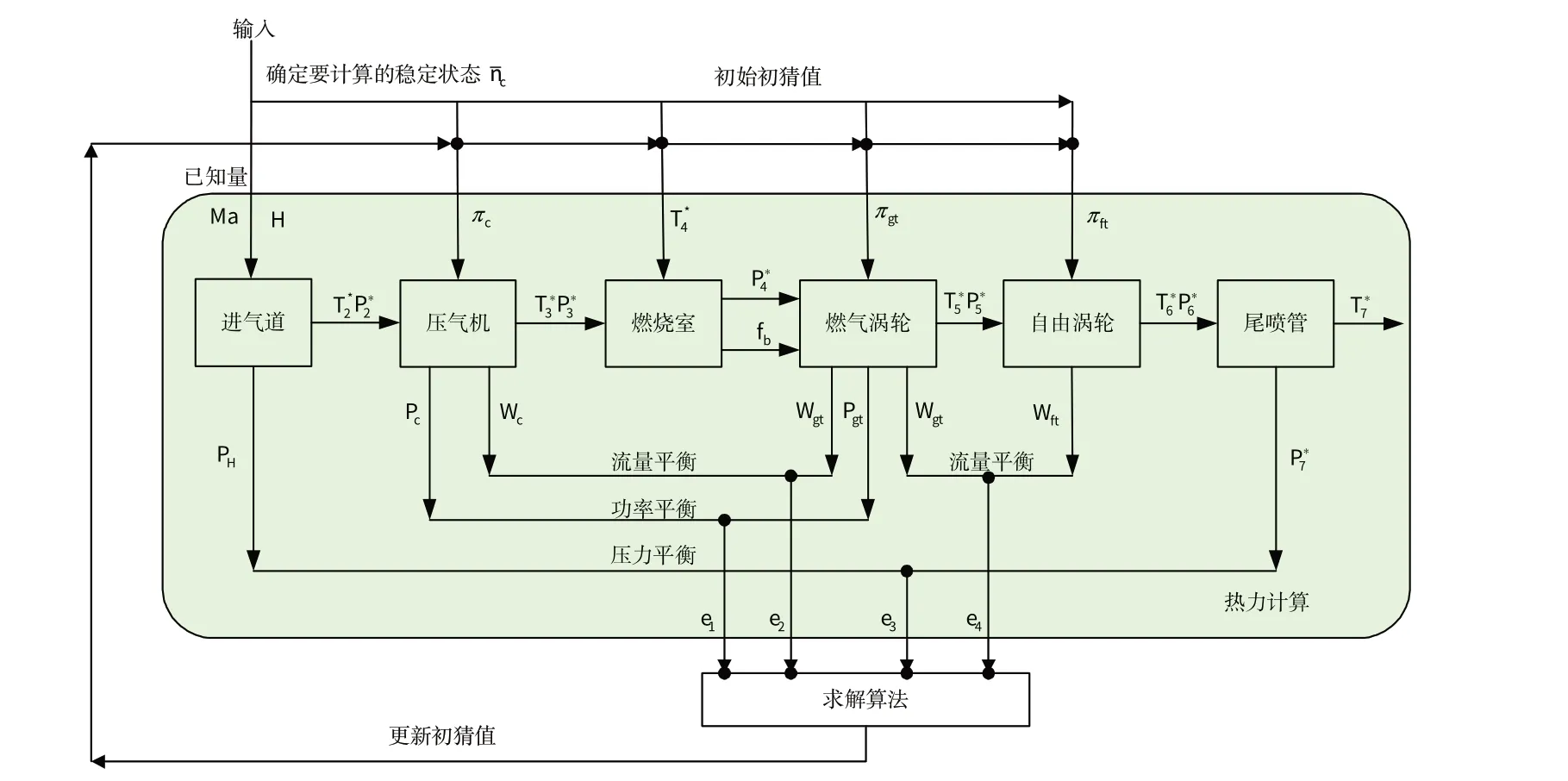
图2 涡轴发动机稳态模型求解示意图Fig.2 Schematic diagram of steady-state model calculation of turboshaft engine

2 混合算法的建立

2.1 N+1点残量法

有n（n=4）个变量的非线性方程组：

记 x=( x1,x2,…,xn)，则 式（2）可 以 写 为fi( x )=0( i =1,2,…,n )。

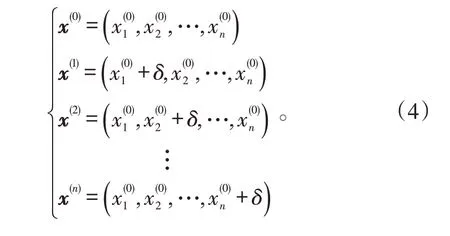
2.2 天牛须算法

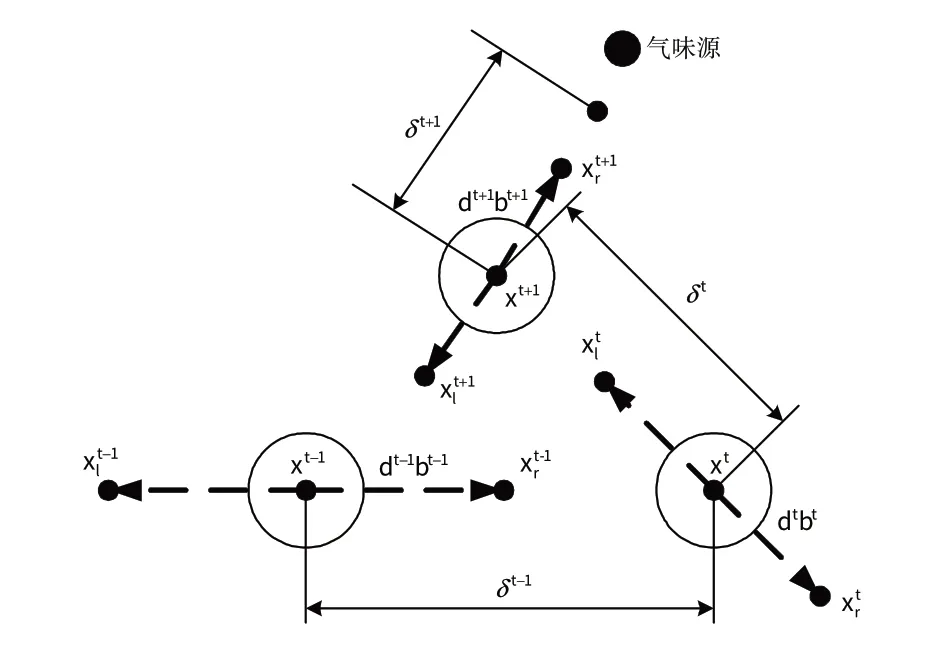
图3 二维空间中的天牛搜索模型示意图Fig.3 Schematic diagram of the beetle antennae search algorithm in two-dimensional space

f( xt)即为发动机模型共同工作方程组的总均方误差ε( xt)，函数的最大值对应的位置即为发动机稳态模型的数值解。为简单描述BAS算法，使用2个规则描述天牛的搜索行为和检测行为。因为天牛会进行随机搜索以探索未知环境，所以定义天牛的搜索方向为一随机方向，用单位向量b 表示：

式（8）中：rand(.)表示随机函数；k 表示天牛位置的维数，真实天牛的位置为3维，本文涡轴发动机模型的维数k=4。

建立天牛左、右触须模型来模仿天牛的搜索过程：

式（9）中：xr、xl分别为右侧、左侧触须的位置；dt为t时刻触须的探测长度，代表该时刻触须的探测能力。

d 的初始值需要足够大小来覆盖适当的搜索区域，从而能够在开始搜索时跳出局部最优点，然后d的值随着时间逐渐减小，以便寻找到最优值。

其次，为了模仿天牛搜索过程中向气味源进行移动的行为，即天牛往左右触须位置中气味浓度高的方向进行移动，建立迭代模型：

式（10）中：δt为t 时刻的移动步长，δ 是关于t 的减函数，δ 的初始值应根据搜索区域确定；sign()· 为符号函数，函数值为1，0或-1。

天牛往气味浓度高的随机触须方向移动一个步长。关于搜索参数的设置，即触须长度d 和移动步长δ，在需要时也可以将这2个参数设为常量，更新规则设计如下：

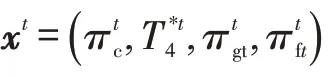
当( t ＜Tmax)或者达到停止条件前执行步骤1）～5）：

1）根据式（8）生成方向向量b；

2）根据式（9）用2种触须在可变空间中搜索；

3）根据式（10）更新状态变量xt；

4）如果f( xt)＜fbest，那么fbest=f( xt)，xbest=xt；

5）根据式（11）、（12）更新探索半径d 和步长δ。

循环终止后返回：xbest、fbest。

2.3 混合算法设计

将基于天牛须算法与N+1 点残量法的求解发动机模型的方法称为BAS-N+1 混合算法，求解流程图如图4所示。

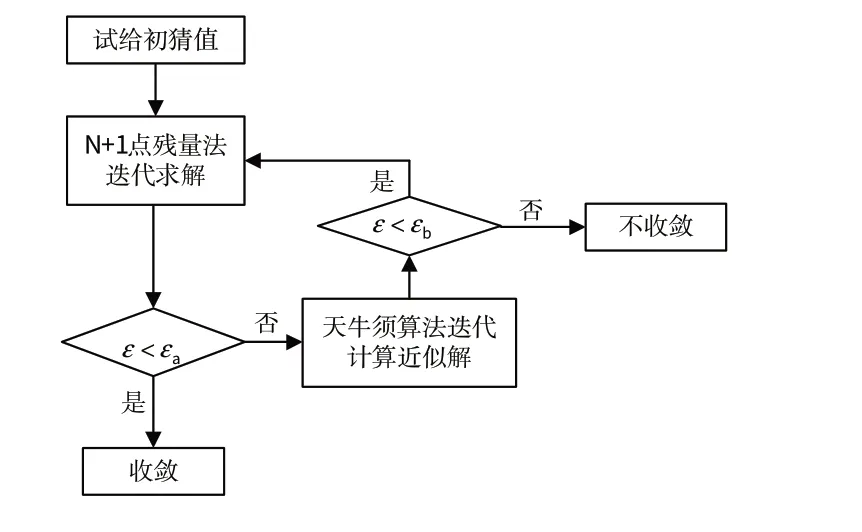
图4 混合算法流程图Fig.4 Flow diagram of the hybrid algorithm

首先，利用N+1 点残量法进行试解，若不收敛则利用BAS 算法得到更接近真实解的近似解；再次，将该近似解代入N+1 点残量法计算。其中，ε 为通过气动热力计算得到共同工作方程组（非线性方程组）总误差，εa为N+1 点残量法的迭代终止误差限制值，εb为BAS算法的误差限制值。

3 仿真和结果分析

求解前，需要合理设置参数变化范围，即4个初猜参数的搜索范围不能过大，过大则会导致特性线插值时超出范围，进而导致程序不收敛。根据已知设计点各参数值和特性线参数范围估计4个未知量的大体范围[19]，如归一化后燃气涡轮前温度的范围一般设置为[0.3,1.02]，其余参数与此类似。在编程处理的过程中，特性线插值的程序需要重点关注并采用一定的技巧[20]，可以采用对插值结果进行边界检测的方式以提高模型的收敛性，将超出边界的插值结果赋予特性线的边界值。

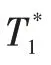
将压气机压比，燃气涡轮前温度，燃气涡轮落压比，自由涡轮落压比的猜值输入模型，BAS 算法主要参数设置如下：总迭代终止误差εa=10-6，迭代误差εb=10-2，步长初始值δ0=2，步长衰减系数0.9，触须长度初始值d0=2，触须衰减系数0.92，PSO算法主要参数设置：粒子数为20，初始惯性权重0.9，最终惯性权重0.6，迭代误差εp=10-2，2种混合算法的求解误差随迭代步数的下降过程如图5所示。

PSO- N+1 混合算法共迭代62 步，终止误差1.828×10-7，平均计算耗时188.275 s，BAS-N+1 混合算法共迭代54 步，终止误差2.751×10-9，平均计算耗时23.901 s。由此可见，BAS-N+1 混合算法拥有比PSO- N+1 混合算法更快的计算速度，这是因为PSO算法粒子数量较多，所以每次迭代的耗时也较长。单纯PSO 算法和BAS 算法要达到所需精度的计算耗时过长，计算量较大。

为验证联合算法求解该型涡轴发动机气动热力学稳态仿真模型的仿真结果，选取试车数据中的燃气涡轮前温度、轴功率、压气机增压比、换算流量作为验证参数（各参数均经归一化），选取最大连续（=0.97）、中间应急（=0.985）和起飞（=1）3个典型状态进行验证。通过已有的7 台发动机的22 次试车数据，选取4 个稳定状态的数据求取平均值对仿真计算结果进行验证，结果见表2所示。

从表2 中可以看出，仿真模型各参数的求解结果与台架试车数据较为接近，3 个状态的各参数仿真结果与台架试车数据的误差保持在3%以内，所以模型是准确可靠的。

不同算法对各参数的计算误差情况如图6 所示，每个算法对发动机不同截面参数的计算误差精度各有高低，但整体误差较为接近。从图5的迭代过程看，BAS-N+1 混合算法具有更好的非线性方程组总误差计算精度，并且其收敛速度也是最快的。

图6 各算法计算误差的对比图Fig.6 Comparison of calculation errors of each algorithm

4 结论

分析仿真结果，并与试车数据对比验证情况后，可以得出以下结论：

1）使用BAS-N+1混合算法求解该涡轴发动机稳态仿真模型能够实现74.85%转速到102%转速范围内收敛，且各参数的求解误差在3%以内。

2）BAS- N+1 算法理论较为简单，容易编程实现。与PSO算法需要超过20个搜索粒子相比，该算法的搜索个体仅有一个，运算量小，收敛速度较快。

3）与PSO- N+1 混合算法相比，BAS- N+1 混合算法求解涡轴发动机稳态模型各参数的计算精度相近，但平均计算时间仅为PSO-N+1混合算法的1/8 左右。