基于MIMU的FastICA算法钻头故障振动信号分析

杨金显 范耀辉

摘  要： 为了解决钻头在钻进过程中由于采集到的信息存在信噪比低和钻头与钻柱振动信号互相混叠而难以对钻头故障振动状态进行有效识别的问题。提出一种基于MIMU的FastICA算法来对钻头与钻柱振动数据进行处理分析，从而放大了钻头振动信号特征（正常、松动），提高了钻头振动信号的识别度。首先对经MIMU采集而来的原始数据进行误差分析和预处理，接着使用FastICA算法进行仿真实验，最后采用预处理后的松动状态下钻头与钻柱的振动信号进行实例实验验证。经验证，此方法有效放大了钻头的振动信号特征，有一定的实际意义。

关键词： 微型惯性测量单元;FastICA算法;钻头;振动信号分析;故障诊断

中图分类号： TM751;TP391.9    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.05.028

本文著录格式：杨金显，范耀辉. 基于MIMU的FastICA算法钻头故障振动信号分析[J]. 软件，2019，40（5）：147153

【Abstract】： In order to solve the problem that the drill bit has low signal-to-noise ratio and the vibration signal of the drill bit and the drill string overlap during the drilling process， it is difficult to effectively identify the fault vibration state of the drill bit. A FastMU algorithm based on MIMU is proposed to process and analyze the vibration data of the drill bit and the drill string， thereby amplifying the vibration signal characteristics of the drill bit （normal and loose） and improving the recognition degree of the vibration signal of the drill bit. Firstly， the error analysis and preprocessing of the original data collected by MIMU are carried out， and then the simulation experiment is carried out by using FastICA algorithm. Finally， the experimental results of the drill bit and the drill string vibration signal under different conditions （normal and loose） are preliminarily verified. It is verified that this algorithm effectively amplifies the vibration signal characteristics of the drill bit and improves the recognition degree of the drill fault vibration signal.

【Key words】： Miniature inertial measurement unit; FastICA algorithm; drill bit; Vibration signal analysis; Fault diagnosis

0  引言

由于在钻井作业时，钻井系统处于复杂的工作环境之中，钻进过程中钻头与钻柱等都会受到各种外界环境因素的影响产生振动，而二者振动的测量信号往往是经过互相混叠互相影响而显现出来的，呈现较为复杂的非线性关系，因此单独有效地提取出能够表现钻头在钻进过程中（正常、松动等）的振动信号就显得犹为必要。

文献[1]使用希尔伯特变换的方法对故障特征进行提取，但却只针对冲击信号有较好的效果，当出现其他故障时，并不能分离得到真实频率。文献[2]通过形态滤波算法进行故障特征提取，但是这种算法在提取故障特征的同时也会过滤低频谐波信号，从而导致提取的故障特征并不完整。文献[3]使用经验模态分解算法进行振动特征信号的提取，但这种算法容易造成模态混叠，分离出的模态物理意义不明确，有可能造成误判或者漏判。独立成分分析（Independent Component Analysis，ICA）是近年来提出的非常有效的数据分析工具，主要用来从混合数据中提取出原始的独立信号，作为信号分离的一种有效方法而受到广泛的关注。这种盲源多通道的信号分析处理技术，对于处理此种多源信号经非线性叠加的情况有着很大的优势。因此本文将以钻井系统中安装在近钻头处与钻柱处的两组微惯性测量器件为研究对象，进行独立成分分析与处理实验，以期实现对钻头处振动信号的分离与提取。而FastICA算法不仅可以对钻头振动混合信号中具有独立性的信号进行有效分离，且运算速度快。故将此算法应用到对钻头故障振动信号的分析中来。

1  數据误差分析

惯性器件的误差包含了常值误差与随机性误差两种不同的误差类型，这里的常值误差通常能够通过建模、测试标定与旋转调制等方式进行误差的补偿，而在经过误差补偿后，无法补偿的确定性误差可以一起归到随机性误差之中。随机误差有着时变性特点，通常是在静态条件下进行测试与分析，然后通过滤波等方式进行消除。在惯性技术领域中，惯性器件的精度通常情况下是指静态条件下的随机性误差，也就是指在最理想条件下，惯性器件所能达到的最高精度[5-10]。

（1）常值误差：常值误差是指在传感器的加速度计输出数据为零时，所得到的数据信息。因此常值误差的多少与传感器的运动情况并无关系，故称其为与陀螺仪和加速度计无关的一种误差。常值误差包括零偏误差、标度因数误差和安装误差等。

（2）随机误差：随机误差是指无法确定的因素所导致的随机漂移，通常有温度漂移、速率随机游走、角度随机游走与偏差不稳定性等。

由上述誤差分析可知，随机性的干扰信号是测量系统的主要误差源之一。因为惯性器件传感器在工作时很容易产生低频的周期性信号，由于这些长周期趋势项的存在，将会造成在二次积分中所得出的位移偏离实际振动轨迹，甚至会产生信号的畸变与失真。因此，通过选用合适的方法消除趋势项与噪声来减少信号中的干扰量是对后续数据进行准确处理的前提与保证。本文主要采用最小二乘法与五点三次平滑法来对采集到的原始钻头振动信号进行降噪处理。

数据经最小二乘法处理可以在一定程度上消除趋势项，主要解决了部分数据偏离基准线的问题，然后再用五点三次平滑法对数据做进一步平滑处理[10-15]。

2  数据预处理

由前面的误差分析得知，随机干扰信号的影响是系统的主要误差源之一。传感器在工作中极易产生低频周期性信号，由于这些长周期趋势项的存在，造成二次积分中得到的位移可能偏离实际运动轨迹较大，甚至产生畸变或失真，因此，减少信号中的干扰成分，采取合适的方法消除趋势项和各种噪声是保证后续数据处理准确的前提。这里主要采用最小二乘法、五点三次平滑法。

2.1  最小二乘法

由图1、图2和图3可看出，数据经最小二乘法处理可以在一定程度上消除趋势项，主要解决了部分数据偏离基准线的问题。但该方法对周期性的干扰信号或不规则的随机干扰信号所引起的尖峰，毛刺现象，处理效果不明显[15-20]。

2.2  五点三次平滑法

下面采用五点三次平滑法对数据做进一步平滑处理。五点三次平滑法是利用最小二乘法的原理，用三次多项式逐次逼近，其计算公式为：

五点三次平滑法适用于时域信号和频域信号，在时域信号处理中，其优点是减小信号中的高频随机噪声，而对频域信号则可以使频谱曲线变得光滑。本文是对时域数据进行处理。

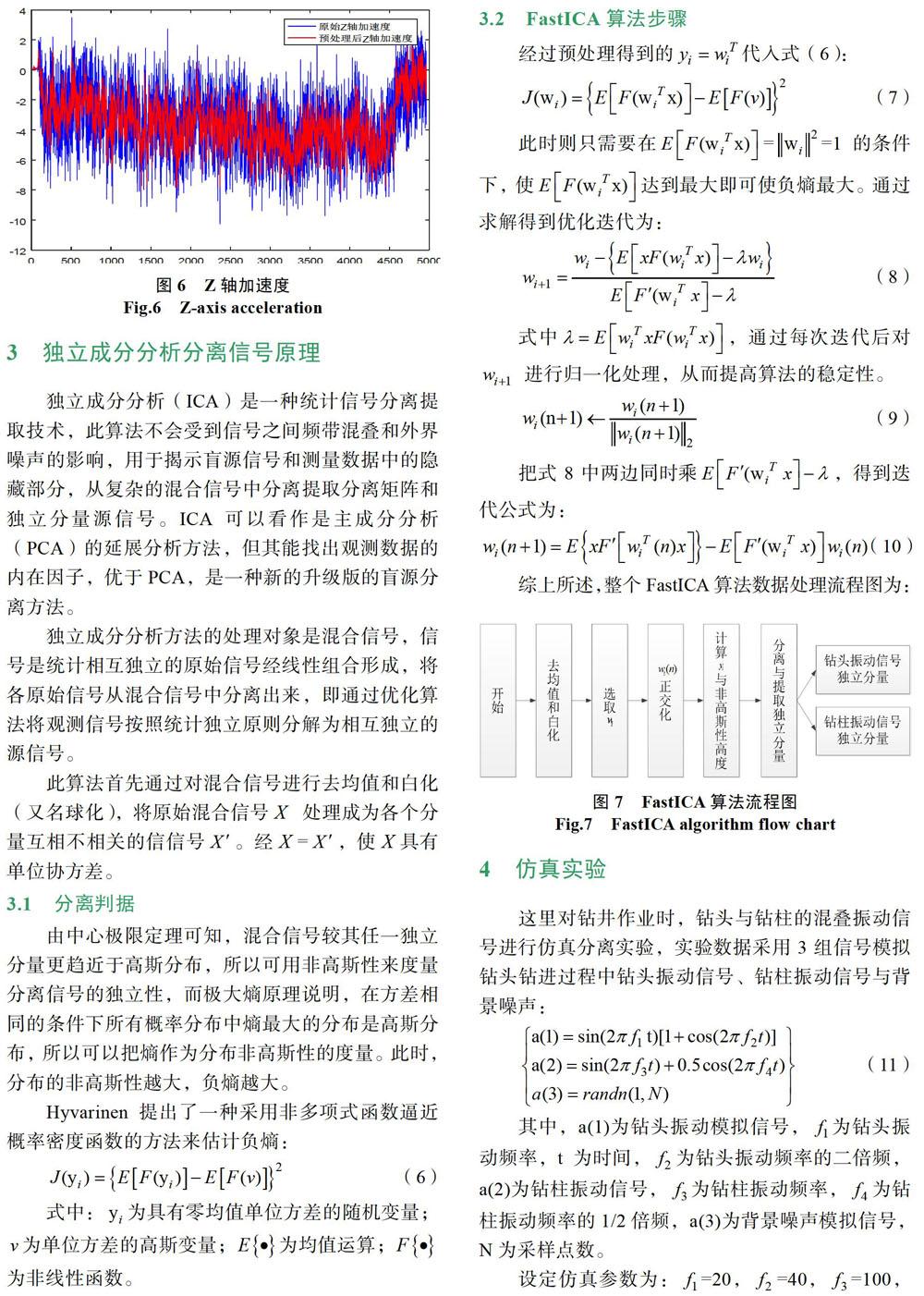
图3、图4与图5分别给出了采用五点三次平滑法滤波前后各轴加速度数据对比情况。

可以看出，经过平滑处理后，周期性的干扰信号或不规则的随机干扰信号所引起的尖峰，毛刺现象的处理效果明显，数据情况得到了很好的改善。

3  独立成分分析分离信号原理

独立成分分析（ICA）是一种统计信号分离提取技术，此算法不会受到信号之间频带混叠和外界噪声的影响，用于揭示盲源信号和测量数据中的隐藏部分，从复杂的混合信号中分离提取分离矩阵和独立分量源信号。ICA可以看作是主成分分析（PCA）的延展分析方法，但其能找出观测数据的内在因子，优于PCA，是一种新的升级版的盲源分离方法。

独立成分分析方法的处理对象是混合信号，信号是统计相互独立的原始信号经线性组合形成，将各原始信号从混合信号中分离出来，即通过优化算法将观测信号按照统计独立原则分解为相互独立的源信号。

此算法首先通过对混合信号进行去均值和白化（又名球化），将原始混合信号  处理成为各个分量互相不相关的信信号 。经 = ，使 具有单位协方差。

3.1  分离判据

由中心极限定理可知，混合信号较其任一独立分量更趋近于高斯分布，所以可用非高斯性来度量分离信号的独立性，而极大熵原理说明，在方差相同的条件下所有概率分布中熵最大的分布是高斯分布，所以可以把熵作为分布非高斯性的度量。此时，分布的非高斯性越大，负熵越大。

接着使用FastICA算法对得到的三组混合信号进行分离，得到各个分离信号如图10示。

对比图8和图10我们不难看出，经Fast ICA算法解混后的三组波形与源信号波形特征除幅值和相位有些许不同，但是其波形特征基本吻合。信号所表达出的物理意义主要体现在其形状上，所以说上述变化不影响对信号的分析，也就是说FastICA算法从混合信号中分离出了具有实际物理意义的特征信号。可知FastICA算法在对钻头故障信号的盲源分离中是可行的。

5  应用实例

以在钻井作业中分别采集的钻头松动运行时钻头、钻柱的横向X轴加速度信号为例。使用第2章预处理方法进行数据的预处理，在进行去均值、白化处理后得到其时域、频域图如图11、图12、图13与图14所示。

经FastICA算法处理前的图11、图12、图13与图14中我们难以在钻头或钻柱的时、频域图中分辨出钻头松动运行时的振动信息，这二者的信号特征互相混叠，并在噪声的影响下几乎难以被发现。经过FastICA算法处理分离后得到的钻头加速度时域、频域图为图15与图16。

对比图8、图12与图9、图13可以清楚得看出，在分离后钻头松动情况下的横向X轴振动信号中，其加速度振动信号时域波形分布较为杂乱，呈现出幅值上的明显上升，且有明显的冲击信号响应。在与此对应的频域图中，波形也显示出了明显的与分离前的不同，频率分布范围更广且特征频率也更加突出、明显。通过对比可以清晰看出在钻井作业中，与钻柱振动加速度信号互相影响混叠的钻头振动加速度信号得到了很好的分离，钻头松动时的振动特征信息在分离后得到了很好的放大与展现。

6  结论

（1）使用最小二乘法和五点三次平滑法对MIMU采集的钻头振动加速度和角速度数据有着很好滤波效果，提高了采集信号的精度。

（2）通过对钻头松动情况下的模拟仿真实验和应用实例，FastICA算法可以很好的分离出钻头的，并且效果显著。很好的验证了在实际工况现场中使用此方法对钻头故障振动信号进行提取的可行性，有一定的实际意义。

（3）在实际应用中，实际采集的复合故障（松动、磨损等并存）情况下的钻头加速度与角速度信号经FastICA方法处理后，并未取得很好的提取效果，此时该算法受到了一定限制，也是今后需要对此算法进行改进的方向。

参考文献

[1] 唐先广， 郭瑜， 丁彦春. 基于独立分量分析与希尔伯特-黄变换的轴承故障特征提取[J]. 振动与冲击， 2011， 15（10）： 45-49.

[2] 李兵， 高敏， 張旭光， 等. 用形态梯度法与非负矩阵分解的齿轮故障诊断[J]. 振动?测试与诊断， 2014， 20（2）： 295-300.

[3] 牛杰， 刘永祥， 秦玉亮， 等. 一种基于经验模态分解的锥体目标雷达微动特征提取新方法[J]. 电子学报， 2011， 20（7）： 1712-1715.

[4] 许德新， 何昆鹏， 梁海波. MEMS惯性测量组件的温度误差补偿模型研究[J]. 哈尔滨工程大学学报， 2010， 31（5）： 607-613.

[5] 刘婷婷， 任兴民， 康召辉. FastICA算法在机械振动信号分离中的应用[J]. 西安工业大学学报， 2008， 14（01）： 27-31.

[6] 查春青， 柳贡慧， 李军， 席岩， 张涛. PDC钻头扭转振动特性分析及减振工具设计[J]. 石油机械， 2017， 45（03）： 1-5.

[7] 张睿， 郑文帅， 黄彬城， 钱坤. 基于FASTICA与PNN的齿轮箱故障诊断研究[J]. 煤矿机械， 2013， 34（06）： 278-280.

[8] 刘刚， 王航， 穆文军. 基于独立成分分析的钻头振动信号识别方法[J]. 科学技术与工程， 2018， 18（16）： 33-37.

[9] 肖国益， 徐进， 祝效华， 胡大梁， 朱礼平， 贾彦杰. 钻头-钻柱系统振动特性分析[J]. 中外能源， 2011， 16（08）： 53-57.

[10] 周云龙， 王锁斌. 高斯矩Fast ICA算法在风机振动信号去噪中的应用[J]. 动力工程学报， 2011， 31（03）： 187-191.

[11] 马斐， 宋淑芳. 钻柱振动诊断方法的研究[J]. 华南理工大学学报（自然科学版）， 1996（12）.

[12] 刘刚， 张家林， 刘闯， 等. 钻头钻进不同介质时的振动信号特征识别研究[J]. 振动与冲击， 2017， 37（8）： 71-78.

[13] 汪攀. 时间序列趋势分析及其在预防性维修中的应用[D]. 武汉科技大学， 2015

[14] 李东文， 熊晓燕， 李博. 振动加速度信号处理探讨[J]. 机电工程技术， 2008， 37（9）： 50-52.

[15] 基于负熵准则盲分离方法的剖析与研究[J]. 丁志中， 叶中付. 系统仿真学报. 2007， 22（13）： 60-63.

[16] PCA与ICA相结合的语音信号盲分离[J]. 王玉静， 于凤芹. 计算机工程与应用. 2012， 16（10）： 31-46

[17] 独立分量分析的原理与应用[M]. 清华大学出版社， 杨福生， 洪波著， 2006

[18] Independent Component Analysis Using an Extended In-fomax Algorithm for Mixed Subgaussian and Supergau-ssian Sources[J] . Te-WonLee， Mark Girolami， Terrence J. Sejnowski. Neural Computation . 1999， 36 （2）： 45-46.

[19] Independent Component Analysis. Hyvarinen A， Karhunen J， Oja E. . 2001， 44（3）： 16-20.

[20] Applica-tion of the Blind Source Separation in Machine FaultDiagnosis： A Review and Prospect. LI Zhi-nong， ， HE Yong-yong， CHU Fu-lei. MechanicalSystems and Signal Processing . 2005， 13（2）： 8-11.

[21] Blind Separation of Sources， Part1： An Adaptive Algorithm Based on Neuromime-tic Architecture. Jutten C， Herault J. Signal Processing . 1991， 27（2）： 13-16.

[22] 张翠平， 苏光大， 人脸识别技术综述[J]， 中国图像图形学报（A版）， 2000， 5 （11）： 885-894.

[23] 张铮， 王艳平， 薛桂香. 数字图像处理与机器视觉[M]. 北京： 人民邮电出版社， 2010.

[24] Javed A. Face Recognition Based on Principal Component Analysis[J]. International Journal of Image， Graphics and Signal Processing （IJIGSP）， 2013， 5（2）： 38.

[25] He Lianghua. Multi-Dimension Principal Component Analysis based on face recognition[J]. The Journal of New Industrialization， 2012， 2（1）： 59-65.

[26] 朱剑， 张锦， 成奋华， 等. 基于支持向量机的人脸识别研究[J]. 计算技术与自动化， 2008， 26（4）： 79-81.

[27] 钟彩. 边缘检测算法在图像预处理中的应用[J]. 软件， 2013， 34（1）： 158-159.

[28] 冯杰， 屈志毅， 李志辉. 基于分类稀疏表示的人脸表情识别[J]. 软件， 2013， 34（11）： 59-61.