协同进化策略的粒子群优化算法

杨蕾 梁永全

摘  要： 为了进一步提高粒子群优化算法的寻优精度，并改善收敛速度慢的问题，本文基于传统的粒子群优化算法，借鉴协同进化的思想和共生机制，提出了将协同进化算法和粒子群算法相结合的算法模型（CEA-PSO）。群体内部采用精英保留策略保留精英个体，将个体的进化和群体之间发生信息交换，达到优势互补的效果。实验结果表明，协同进化策略的粒子群优化算法精度更高，优化性能更佳。

關键词： 协同进化;粒子群优化算法;精英保留策略

中图分类号： TP301.6    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.08.036

本文著录格式：杨蕾，梁永全. 协同进化策略的粒子群优化算法[J]. 软件，2019，40（8）：152155

【Abstract】： In order to further improve the optimization precision of the particle swarm optimization algorithm and improve the convergence speed. Based on the traditional particle swarm optimization algorithm， this paper proposes an algorithm model （CEA-PSO） combining co-evolution algorithm and particle swarm optimization algorithm with reference to the idea of co-evolution and symbiosis. Elite retention strategies are used within the group to retain elite individuals， information exchange occurs between the evolution of individuals and groups to achieve complementary effects. The experimental results show that the particle swarm optimization algorithm base on co-evolution strategy has higher precision and better optimization performance.

【Key words】： Co-evolution; Particle swarm optimization; Elite retention strategy

0  引言

随着社会经济和信息技术的快速发展，各个领域中的问题都可以通过将待决解决问题转化为优化问题来处理，目前存在的优化算法大致可以分为两类：传统优化算法和智能优化算法。传统优化算法一般是针对结构化的问题，有较为明确的问题和条件描述，如线性规划，二次规划，整数规划，混合规划，带约束和不带约束条件等，即有清晰的结构信息;现代智能优化算法主要包括差分进化算法 （Differential evolutionary， DE）[1]、粒子群算法（Particle swarm optimization， PSO）[2，3]、遗传算法（Genetic algorithm， GA）[4]、蚁群算法（Ant colony optimization， ACO）[5]、人工蜂群算法（Arti?cial bee colony， ABC）[6]等。协同进化算法[7]（Co-Evolutionary Algorithm， CEA）是研宄者在协同进化理论基础上提出的一类新算法。这类算法强调了在进化过程中种群内部的相互影响和种群之间的相互协调。这些年来，许多专家学者提出了多种多样的CEA，较主流的划分[8]：竞争型协同进化算法（Competitive Co-Evolutionary Algorithm， Com-CEA）[9]和合作型协同进化算法（Cooperative Co-Evolutionary Algorithm， Coo-CEA）[10]两类。

粒子群优化算法基于迭代策略，粒子在解空间中对最优解进行搜索，计算简单，已经广泛应用在工程优化、神经网络训练、图像处理等领域[11-13]。但是在寻优精度和收敛速度上有待提高，为解决上述问题，专家学者们进行了各种实验研究。Asmara 等[14]法的基提出了一种快速的粒子群协同进化优化算法，提高了算法的收敛速度。Zhang等[15]提出一种多粒子协同进化算法解决多目标优化问题。寻优精度和收敛有了很大提升，但还是有改进空间。

针对这两个问题，本文在粒子群算法的基础上，借鉴合作型协同进化的思想和共生机制，提出了将协同进化算法和粒子群算法相结合的算法模型。用实验结果证明本文算法能改善基本PSO算法中收敛速度慢的问题。

1  概述

1.1  协同进化算法

在协同进化理论中，协同模型的主要思想是直接将群体中的个体划分为若干子群体，每一子群体代表解空间中的一个子区域（子空间），其中的每一个体均代表问题的一个解。所有子群体并行展开局部搜索，所搜索到的优良个体将在不同子群体间进行迁移，作为共享信息指导进化的进行，从而有效提高算法的全局收敛效率。

在传统进化算法中[16-18]，个体的适应度由个体的染色体决定，是一种绝对适应度，没有考虑到个体之间的协同影响以及种群之间的复杂关系;而在协同进化算法中，考虑了种群内部中个体之间的相互影响以及种群之间在进化过程中的相互协调，个体的适应度由个体与周围个体发生协同关系时的表现决定，是一种相对适应度。协同进化算法具有更的自适应性，能够克服传统的进化算法中常见的早熟收敛等现象，具有广阔的应用前景。合作型协同进化流程图如图1所示。

1.2  粒子群优化算法

PSO算法通过种群中个体的相互协作搜索寻优空间，确定最优目标，实现问题优化。PSO算法中，粒子群体包含的任意无质量粒子 的运动状态由位置向量 和速度向量   表示。其中，D表示决策变量的个数; ，N是种群的粒子个数。 搜索时，根据更新粒子的速度和位置。

其中：k表示粒子的搜索迭代次数; 表示搜索的惯性权重系数; ，表示学习因子; 和 是均匀分布在区间[0，1]内的随机数; 是粒子 的个体最优解，称为个体极值; 是目前种群搜索到的最优解，称为全局极值[19-20]。

粒子群算法步骤如下：

（1）设置种群规模N、变量范围R、惯性权重系数ω、学习因子 和 ，在给定搜索空间内随机初始化包含速度和位置信息的粒子;

（2）计算每个粒子的适应度，设置粒子 的适应度值为其当前的个体极值 ，最好粒子为全局极值 ;

（3）根据式（2）更新每个粒子的速度和位置;

（4）更新后，比较每个粒子 的函数值与其个体极值 ，若函数值较优，则设置该函数值为个体极值;再比较全局极值与全部个体极值，获得最新全局极值 ;

（5）判断是否满足给定的终止条件，若满足，则终止搜索，输出优化结果;否則，返回步骤（3）继续搜索。

2  基于协同进化策略的粒子群优化算法

2.1  算法的基本思想

协同进化策略的粒子群优化算法在基于传统粒子群算法的基础上，借鉴协同进化的思想和共生机制，提出了将协同进化算法和粒子群算法相结合的算法模型，将个体的进化与群体联系起来。

2.2  协同进化策略的粒子群优化算法描述

在协同进化粒子群优化算法中，多个种群有相同的搜索空间，群体内部采用精英保留策略来保留精英个体，进化机制采用传统的进化算法，协同进化粒子群优化算法主要在于个体的进化与群体之间有一定的关联，将个体的进化和群体之间发生信息交换，达到优势互补的效果。

协同进化粒子群优化算法的实现步骤如下：

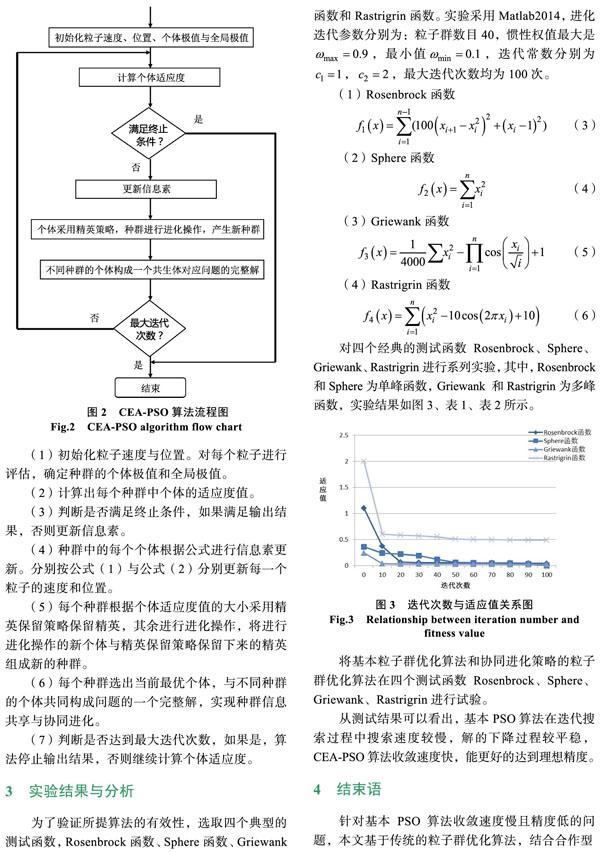
（1）初始化粒子速度与位置。对每个粒子进行评估，确定种群的个体极值和全局极值。

（2）计算出每个种群中个体的适应度值。

（3）判断是否满足终止条件，如果满足输出结果，否则更新信息素。

（4）种群中的每个个体根据公式进行信息素更新。分别按公式（1）与公式（2）分别更新每一个粒子的速度和位置。

（5）每个种群根据个体适应度值的大小采用精英保留策略保留精英，其余进行进化操作，将进行进化操作的新个体与精英保留策略保留下来的精英组成新的种群。

（6）每个种群选出当前最优个体，与不同种群的个体共同构成问题的一个完整解，实现种群信息共享与协同进化。

（7）判断是否达到最大迭代次数，如果是，算法停止输出结果，否则继续计算个体适应度。

3  实验结果与分析

为了验证所提算法的有效性，选取四个典型的测试函数，Rosenbrock函数、Sphere函数、Griewank 函数和Rastrigrin函数。实验采用Matlab2014，进化迭代参数分别为：粒子群数目40，惯性权值最大是 ，最小值 ，迭代常数分别为 ， ，最大迭代次数均为100次。

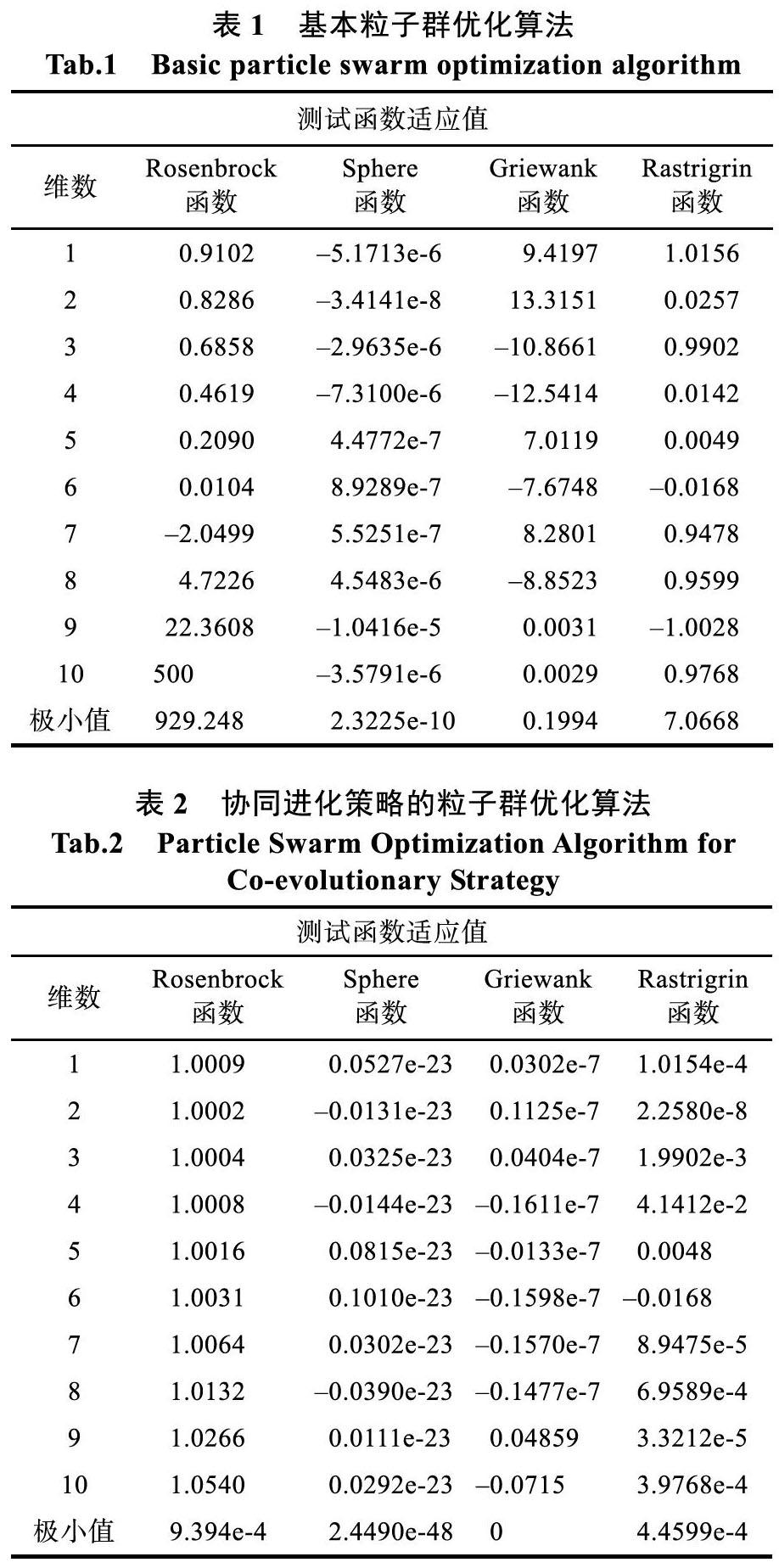
对四个经典的测试函数Rosenbrock、Sphere、Griewank、Rastrigrin进行系列实验，其中，Rosenbrock和Sphere为单峰函数，Griewank 和Rastrigrin为多峰函数，实验结果如图3、表1、表2所示。

将基本粒子群优化算法和协同进化策略的粒子群优化算法在四个测试函数Rosenbrock、Sphere、Griewank、Rastrigrin进行试验。

从测试结果可以看出，基本PSO算法在迭代搜索过程中搜索速度较慢，解的下降过程较平稳，CEA-PSO算法收敛速度快，能更好的达到理想精度。

4  结束语

针对基本PSO算法收敛速度慢且精度低的问题，本文基于传统的粒子群优化算法，结合合作型协同进化理论，对算法进行改进，并与基本粒子群优化算法进行比较，提出了一种基于协同策略的粒子群优化算法，该算法采用精英保留策略，将个体的进化和群体之间发生信息交换。几组经典的基准测试函数表明，本文所提出的优化算法在优化性能和收敛速度方面有很好的效果。

参考文献

[1] Das S， Mullick S S， Suganthan P N. Recent advances in differential evolution-An updated survey. Swarm & Evolu- tionary Computation， 2016， 27： 1-30.

[2] Duan H B， Li P， Yu Y X. A predator-prey particle swarm op-timization approach to multiple UCAV air combat modeled by dynamic game theory. IEEE/CAA Journal of Automat- ica Sinica， 2015， 2（1）： 11-18.

[3] Pan Feng， Chen Jie， Gan Ming-Gang， Cai Tao， Tu Xu-Yan. Model analysis of particle swarm optimizer. Acta Automat- ica Sinica， 2006， 32（3）： 368-377.

[4] Long Q， Wu C Z. A hybrid method combining genetic algo-rithm and Hooke-Jeeves method for constrained global op-timization. Journal of Industrial & Management Optimiza-tion， 2017， 10（4）： 1279-1296.

[5] Prakasam A， Savarimuthu N. Metaheuristic algorithms and probabilistic behaviour： a comprehensive analysis of Ant Colony Optimization and its variants. Arti?cial Intelligence Review， 2016， 45（1）： 97-130.

[6] Ma L B， Zhu Y L， Zhang D Y， Niu B. A hybrid approach to arti?cial bee colony algorithm. Neural Computing and Applications， 2016， 27（2）： 387-409.

[7] 李碧， 林土胜. 协同进化在遗传算法中的应用述评[J]. 计算机科学， 2009， 36（04）： 34-37+63.

[8] 慕彩红. 协同进化数值优化算法及其应用研究[D]. 西安电子科技大学， 2010

[9] 聂敬云， 李春青， 李威威， 等. 关于遗传算法优化的最小二乘支持向量机在MBR仿真预测中的研究[J]. 软件， 2015， 36（5）： 40-44.

[10] Zhou H， Wang J. A Cooperative Coevolutionary Algorithm with Application to Job Shop Scheduling Problem[C]. IEEE International Conference on Service Operations and Logistics， and Informatics. IEEE， 2007： 746-751.

[11] 丁知平. 量子混沌自适应粒子群优化算法的研究[J]. 软件， 2018， 39（4）： 09-14.

[12] Wang GL， Zhao GQ， Li HP. Research on optimization design of  the heating/cooling channels for rapid heat cycle moldingbased on response surface methodology and constrained particle swarm optimization. Expert Systems with Applications， 2011， 38（6）： 6705-6719.

[13] Gorai A， Ghosh A. Hue-preserving color image enhancement using particle swarm optimization. 2011 IEEE Recent Advances in Intelligent Computational Systems. Piscataway. IEEE. 2011. 563-568.

[14] Asmara A， Krohling RA， Hoffmann F. Parameter tuning of a computed-torque controller for a 5 degree of freedom robot arm using co-evolutionary particle swarm optimization. Proc. IEEE Conference on Swarm Intelligence Symposium. Pasadena， USA. June. 8-10， 2005. 162-168.

[15] Zhang Y， Gong DW， Ding ZH. Handling multi-objective optimization problems with a multi-swarm  cooperative particle swarm optimizer. Expert Systems with Applications. 2011， 38（11）： 13933-13941.

[16] 刘露萍， 贾文生. 基于方体剖分和量子免疫粒子群算法的Nash均衡求解[J]. 软件， 2018 ， 39（6）： 01-03.

[17] 陈骁睿. 基于改进粒子群算法的机位分配问题研究[J]. 軟件， 2015， 36（1）： 72-76.

[18] 肖根福， 刘欢， 李东洋， 欧阳春娟. 一种求解大规模问题的自学习协同粒子群算法[J]. 井冈山大学学报（自然科学版）， 2018， 39（03）： 32-37.

[19] 李俊， 汪冲， 李波， 方国康. 基于多策略协同作用的粒子群优化算法[J]. 计算机应用， 2016， 36（03）： 681-686.

[20] 李垒， 岳小冰. 一种多粒子群协同进化算法[J]. 计算机系统应用， 2015， 24（09）： 156-159.