基于Matlab的分形理论在医学中的应用研究

俞凯君 李春

摘  要： 分形几何已经在各种领域得到广泛应用，分形分析是一种功能强大但仍未充分利用的数学工具。分形理论与医学的实际应用之间的联系是分形维数（FD）。本文介绍了分形和分形维的概念，基于Matlab以心图形为例说明盒维数的计算过程。在此基础上，就分形理论在心血管系统、肺部肿瘤、胎儿监护、中医等医学领域的近期研究进展作一回顾。结论：分形理论对于描述生物系统在任何水平的非常复杂的结构和行为非常有用，它也为非侵入性定量医学诊断提供了一种实用的工具。

关键词： 分形理论;医学;分形维;研究进展

中图分类号： R-1;TP39    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.08.027

本文著录格式：俞凯君，李春. 基于Matlab的分形理论在医学中的应用研究[J]. 软件，2019，40（8）：111116

【Abstract】： Fractal analysis is a powerful but still underutilized mathematical tool that has been widely used in various fields. The link between fractal theory and the practical application of medicine is the fractal dimension （FD）. This paper introduces the concept of fractal and fractal dimension， taking the ECG as an example to illustrate the calculation process of box dimension based on Matlab. In this paper， the recent research progress of fractal theory in the medical fields such as cardiovascular system， lung tumor， fetal monitoring， and traditional Chinese medicine were reviewed. Fractal theory is useful for describing very complex structures and behaviors of biological systems at any level， and it also provides a practical tool for non-invasive quantitative medical diagnosis.

【Key words】： Fractal theory; Medical; Fractal dimension

0  引言

上世纪70年代由Benoit Mandelbrot创立的分形（fractal）理论是当今非线性科学的前沿课题，并被广泛应用于自然科学和社会科学的诸多领域。作为“大自然的几何学”[1]，分形的特征在于三个属性：首先，自相似性，其中任何一小部分對象都是整体的精确复制品;其次，缩放分形在多个尺度上看起来是相同的（例如，在微观和宏观层面），这个属性通常被称为“尺度不变性”;第三，它们具有分数（非整数）维度。Weibel认为分形是生物有机体的设计原则，分形设计在结构和功能上都是很有效的，因为它需要很少的能量来维持自身[2]。因此，在自然界中随处可见分形结构并不奇怪。天然分形的例子包括云，河网，断层线，山脉，雪花，水晶，闪电，花椰菜，西兰花和海浪[3]。分形模式也无处不在：数学[4]，工业[5]，股票市场[6]，气候科学[7]，星系[8]，甚至我们观看的电影和玩的游戏[9，10]。

人体结构是复杂的，包括呼吸道和支气管分枝、部分心脏、肾脏系统、血管树、毛细血管网、DNA、心跳、步态模式、心肌电传导网[11]等……这些结构和生理系统具有几何和功能的复杂性，具有分形特征。表征这些器官的一个精确的方法是通过数学建模，然而，只适用于光滑和规则形状情况的欧氏几何学无法解决这些问题， 因为在平直的欧式空间中维数是自然数[12]。在分形研究中，分形维数是定量描述分形的基本参量，它是标度变换下的不变量[13]。对于非线性系统，其分形维数通常是一个介于整数之间的分数或小数，并且超过它的拓扑维数。正是分形的这种特异性，所以它才在医学领域中具有巨大的作用[14]。

1  分形与分形维

一般把在形态（结构）、功能和信息等方面具有自相似的研究对象统称为“广义分形”，把研究分形性质及其应用的科学统称为“分形理论”[15]。

关于分形的准确定义，至今仍没有得到统一。Mandelbrot在1986年提出了一个比较实用的定义[16]，即：组成部分以某种方式与整体相似的形，称为分形。目前使用较多的是K. Falconner对分形的描述[17]（Kenneth Falconer，）：

（1）分形具有精细的结构和细节;

（2）分形极不规则，无法用欧式几何理论进行描述;

（3）分形具有统计意义上的自相似性，局部与整体之间呈现出高度的一致性;

（4）以特定的方式定义的分形，通常其分形维数大于其拓扑维;

（5）在许多情况下，分形可以通过迭代、递归等方式生成。

分形理论与实际医学应用之间的联系是分形维数（FD）。维数是几何对象的一个重要特征量，直观地说，维数是为了确定几何对象中一个点的位置所需的独立坐标的数目，也即独立方向的数目。在分形研究中，分形维数通常是一个介于整数之间的分数或小数。曲线的拓扑维为1，而随着复杂程度增加，不同类型曲线的分形维的大小也不同，如下图1。

分形维数以数值形式描述复杂事物的分形特征，既可以通过数值对事物的分形特征做定量判断和区分，也可以通过具体数值对不同的事物进行分形特征分析[18]，因此其特点是方便、简洁且直观。这为分形的应用提供了十分有效的途径及非常广阔的空间。

分形维数的定义有很多种：盒维数、关联维数、自相似维数、豪斯道夫（Hausdoeff）维数、信息维数及李雅普诺夫（Lyapunov）维数等[19]。在医学应用方面，以盒维数的应用最为普遍。

1994年，基于Mandelbort的分形几何理论，Sarkar与Chaudhuri提出了盒维数定义及算法这为包括医学研究在内的非线性科学提供了新的思路，盒维数的基本定义是[20]：假设P是二维平面内任意一个非空有界子集，对于任意一个 ， 表示用来覆盖P所需边长为 的盒子数。若存在一个参数 ，使得当 时：

盒维数的出现，使得医学研究中的非线性复杂问题的定量研究成为可能。经过短短几十年的发展，分形在心脏病学、肺部肿瘤医学、中医学及胎儿脐血流多普勒信号等复杂的非线性醫学领域得到了很好的应用。

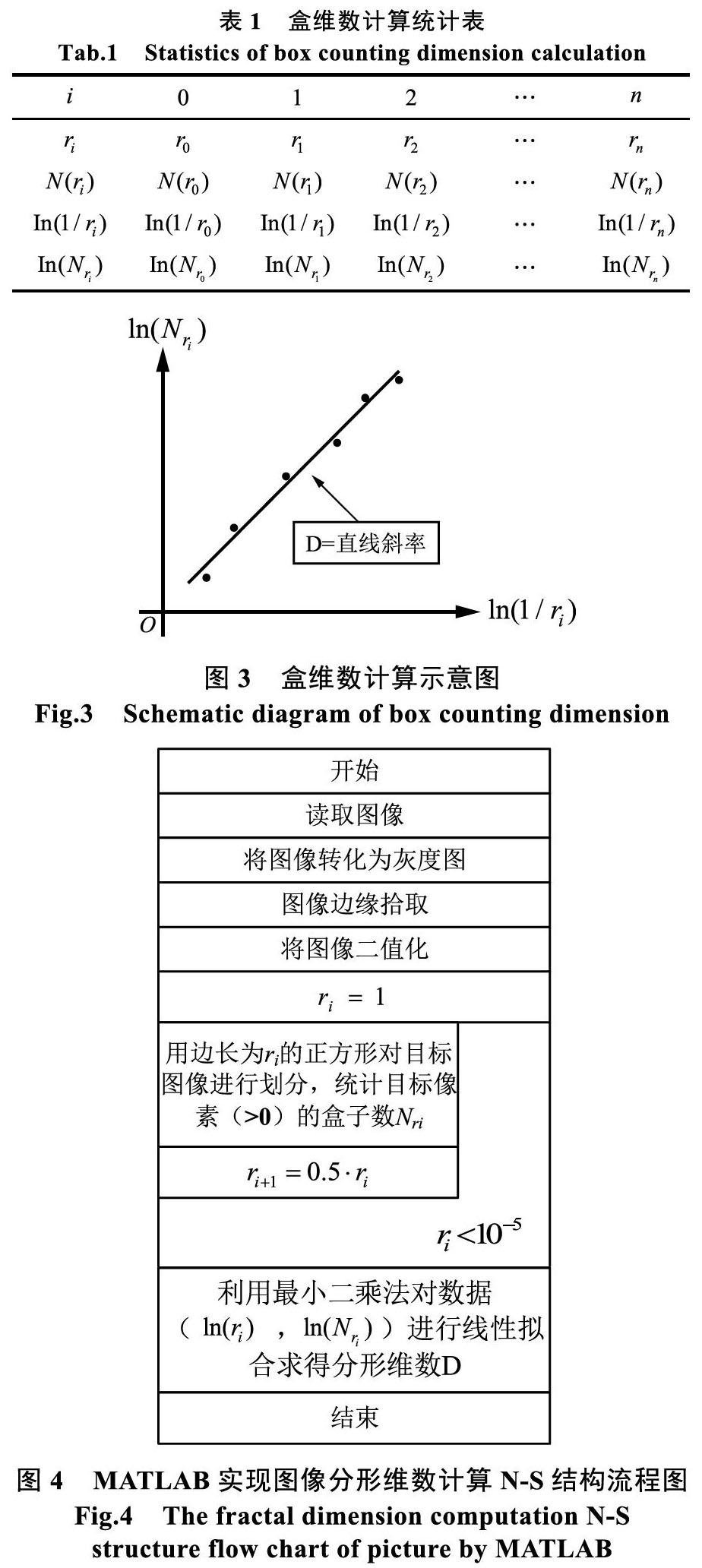
如图2，以心图形为例说明计算实现分形维数计算过程：用尺度 的逐渐缩小的正方形网格覆盖心电图。具体算法为：先选择一系列边长大小为 盒子对图形进行覆盖，计算出覆盖住分形体的盒子数目 ，不断缩小尺度 ，得出一系列不同尺度 对应的 和 ，如表1所示。

然后，根据数据组（ ， ），采用最小二乘法线性拟合并在双对数坐标中画出直线，其斜率即为分形维数 ，如图3所示。

根据盒子计数算法，基于matlab软件编写程序计算程序，其算法逻辑的N-S结构流程如图4。

2  分形与心脏病学

用于研究心脏生理信号的主分形方法（两种单分形和一种多重分形）主要有以下三种，分别是：（1）使用傅里叶方法的幂律分析，该分析方法可以评估心跳间隔以产生功率谱密度（PSD）提取心律中的频率谐波;（2）去趋势波动分析（DFA），它测量嵌入在心跳间隔内的时间尺度之间的相关程度，即：它表征时域中的幂律缩放;（3）多重分形分析，其假设异质心率信号的不同子部分由局部特征表征，每个子部分具有不同的分形维FD（它还表征时域中的幂律缩放）。虽然这些方法的操作域（频率与时间）不同，但它们的分形测量确实相互关联，并且以简单的方式与总体FD相关[21]。

在心脏电生理学中，需要将体内成像技术与计算机建模相结合以精确地重建复杂人体Purkinje网络的3D几何结构，这些技术可以支持单心室或双心室起搏，射频消融和心脏除颤的个性化策略的设计。Purkinje网络的手动生成相当复杂，并且十分耗时，因此电生理学家和生物工程师已经合作开发分形树算法，以更真实地模拟人类心脏博动序列[22]。

最新研究表明分形维（FD）可能在临床超声心动图中发挥作用，分形分析已经应用于经胸超声心动图图像。例如，一项研究使用基于纹理特征提取来自动检测心肌梗死区域[23]，“Texton”指的是自然图像中的基本微观结构或与人类视觉感知相关的图像纹理的微妙结构[24]。该研究使用的算法检查了心脏的单个超声心动图视图中的微小像素变化，它总共使用了八个特征，其中一个特征基于分形分析，将表面粗糙度测量为分形维（FD）[25]。160名患者（50%患有梗死）的结果特别有希望，因为该方法是自动化的，需要操作员手动定义要评估的图像部分。

心脏生理学分析方面，嵌入健康人体心率和血压功率谱的信号是随着时间的推移具有三个功率分量的特征频率状态：反映呼吸波动的高频分量，低频分量和非常低频分量。这些复杂信号中的不规则性可以用分形测量定量描述，它们在多个水平上可以自主调制[26]。通常，心率变异性的丧失预示着更高的死亡率[27]，结果有助于心脏病的诊断、表征和分类，了解患者的不良事件风险（恶性和非恶性心律失常，心源性猝死）。

3  分形在肺部肿瘤的应用

肿瘤是以细胞异常增殖为特点的一大类疾病，常在机体局部形成肿块。肿瘤生长的随机性使其呈现出不规则的形状[28]，用分形理论对肿瘤进行描述，成为医生判断肿瘤恶变程度的一个有效指标[29]。更为重要的是，使用分形分析能够在整体肿瘤大小或体积发生任何可检测的变化之前检测分形维（FD）的变化，对肿瘤内部微血管和外部轮廓分形维（FD）值的测定可作为肿瘤发生发展的临床指标之一，对肿瘤的预测和治疗评价有重要的意义[30-32]。

Al-Kadi[33]提出了一种计算机辅助决策支持系统，用于分析脑肿瘤的组织病理学图像。该分析方法首先将图像分解成小波包，每个小包表示不同的长度尺度。小波分解是一种类似于更常见的傅里叶变换的数学表示：在后者中，“信号”根据不同空间频率（长度尺度）的正弦和余弦进行分解;在前者中，使用小波代替，小波是更广义的振荡函数，可以形成完整的正交集（包），并可用于表示数据。然后可以使用分形分析来选择表示最佳图像的区别特征的一组分组。图像的傅立叶变换的结果本身是图像，但是在傅立叶空间中，也称为k空间。以类似的方式，图像的小波分解产生进一步的图像，每个小波包产生不同的图像，然后使用分形几何来分析这些第二代图像，以确定哪个包更完整和准确地描述原始医学图像。这种方法强调分形分析不仅可以应用于原始图像或最小处理图像，而且可以应用于从它们派生的高阶数据集。此外，该方法消除了对二值图像的需要并保留了关于组织纹理的更多信息。上述方法可以很容易地应用于未来肺肿瘤组织病理学样本的研究。实际上，基于与多种癌症类型相关的这些报告，分形分析在肺癌组织病理学中的应用有可能提供关于癌症的多个方面的临床相关信息，包括血管形成，恶性肿瘤，甚至患者预后。

4  分形在中医的应用

人们所看到的系统尤其是生命系统的复杂性可想而知，现代医学中简单的线性思维并不能解读这一问题，而中医却具有分线性思维的分形特点[34]。

黄雁南[34]探讨了分形几何学、分形生理学和人体穴位分布的分形结构。汪慧敏[36]对人体穴位皮肤电的分维研究。

徐天成等[37-38]使用分形理论实现经络数字化方法对经络内涵的另一种方法，其做法是：基于传统经络腧穴学，引入混沌理论，应用分形几何学，提出数字经络的概念;以临床常用的心经、脾经等经络穴位为基本单元，遵循自相似法则构建数学公式，以C++语言编写程序，绘制6条经络主干的分形化经络循行线，创建数字经络;并提出检验的实验方法，实验得到部分传统经络的体表循行路径可用数学方法表达，基于这种表达的计算机程序实现了 6条经络的数字化，数字化的经络呈现出传统经络未表达的细节。可见：混沌及相关理论技术是构建数字经络的重要途径之一，传统经络理论可实现数字化。

周德生等[39]利用分形理论将脑藏象理论分为脑髓脑室-脑脏腑系统、脑脉脑络-脑经脉系统、官窍神窍-脑窍系统、泥丸九宫-脑神机系统、脑气脑血脑脊液-脑精气系统等5个方面。这种区别于功能神经学及神经生理学的脑藏象理论，从整体观和分形观角度阐释脑功能的复杂性和实用性，形成一个中医药一体化语言系统平台，能够为中医脑科临床应用提供中医特有的思维策略，开拓新的治疗思路。

张季等[40]以分形理论为基础设计实现计算数字化舌图分形维数的算法，并运用这一算法计算标准环境下采集的431例数字化舌图样本数据分形维数。研究得出验证结论：分形维数可作为数字化舌象纹理分析的有效参考参数，因其对舌苔的厚薄、腐腻等数字化舌图图像特征敏感，在增加样本量的基础上有望实现分类标准的制定。

5  分形在胎儿监护的应用

采用分形理论对胎儿心率和脐动脉血流多普勒信号进行分析，对于实时监测孕妇及胎儿健康状态具有十分重要的理论意义和应用价值[41-43]。

通过胎儿监测获得的心率模式的解释依赖于基线的定义，该基线被认为是胎儿休息期间缺乏外部刺激时的连续平均心率。J.C. Echeverriaa[44]提出了基线波动的妊娠研究，涉及分形和非线性特性，以根据成熟的监护机制引入的时变基线水平来评估这些波动。晚上长时间记录（>6 h）时，每周从17至38周检查一次低危妊娠。胎兒平均心率样本和相应的基线系列从原始腹部ECG非卧床数据获得。应用去趋势波动分析对这些系列数据进行分形特征评价。还可通过应用缩放量和符号分析来探索基线系列以评估非线性特征和时间序列。研究的主要发现是：基线显示分形特征甚至非线性反相关波动特性，妊娠中期出现这种情况（甚至更早期这种情况尤其如此）。妊娠30周后变得明显更复杂，结构化（即非随机）波动和特定的非线性变化表明，基线提供了有关心脏调节机制功能整合的信息。

Spilka，等[45]利用分形理论对胎儿心率进行非线性特征分类，将常规方法和非线性特征方法对217个胎儿心率记录信号进行分析。研究结果表明：非线性特征的增加提高了分类的准确性。进一步评估了常规胎心率特征，并将其与非线性特征进行了比较，以、以此分析出产时胎儿心率（FHR）分类的重要性。研究证明，增加非线性特征可以提高胎心率分类的准确性。使用常规和非线性特征的组合来实现最佳分类结果，灵敏度为73.4%，特异性为76.3%，F-测量为71.9%。选择最佳的非线性特征是：Lempel Ziv复杂性，样本熵和通过Higuchi方法估计的分形维数。由于自动胎心信号评估的结果比较容易重现，因此胎儿心率（FHR）评估的过程可能会变得更加客观，并且可能使临床医生能够专注于在分娩过程中影响胎儿的其他非心率方面的参数。

在分形理论对脐动脉血流多普勒信号分析研究方面，Kara S等[46]对20名孕期为18到20周的胎儿脐动脉多普勒血流信号记录，基于豪斯特指数的正常孕期脐动脉多普勒信号的分形分析。结果显示：从分形维曲线上得到的多普勒参数比从最大速度曲线上获得的多普勒参数敏感，因此，分形维技术可以改善血流速度变化的检测。为了证明分数维是一项较好的脐动脉血流参数，吴晓峰等[47]通过对100多例胎儿脐血流信号的分析研究，计算了心动周期内超声多普勒音频信号的分维值，并对超声多普勒信号的分维特征进行统计分析，结果表明：分维值对某些病症具有敏感性，甚至优于现有的声谱参数法。Latifo?lu F等[48]记录来自20名妊娠18至20周正常妊娠妇女的脐动脉的多普勒信号，并使用Hurst指数计算分形维数曲线。其中，RI、PI和S / D指数是根据多普勒超声波图的最大频率包络和分形维数曲线计算出来的，结果表明：从分形维数曲线得到的多普勒指数与从最大速度曲线得到的多普勒指数一样敏感。PSD（HURST）指数比传统的多普勒指数更灵敏地检测血流变化。

6  总结

分形理论在医学上的应用远不止以上几个方面，如在医学影像多重分形分析图像分析（包括边缘检测、图像分形压缩、图像分割、图像识别、纹理分析）[49]、心律失常和脑电信号的多重分形去趋势波动分析、视网膜图像识别、糖尿病视网膜病变等更为广阔的领域均已有很大的研究进展。

分形几何对于描述生物系统在任何水平的非常复杂的结构和行为非常有用[50]，分形理论也为非侵入性定量医学诊断提供了一种实用的工具。

参考文献

[1] Mandelbrot， B. B. The Fractal Geometry of Nature （W.H. Freeman and Company， 1982）.

[2] Weibel E R. Design of Biological Organisms and Fractal Geometry[C]//Fractals in Biology & Medicine. 1994.

[3] Bhattacharya S， Malyavantham K S， Acharya R， et al. Fractal analysis of replication site images of the human cell nucleus[C]// International Conference of the IEEE Engineering in Medicine & Biology Society. 2005.

[4] Falconer K. Fractal Geometry： Mathematical Foundations and Applications， 3rd Edition[M]. Wiley， 2003.

[5] Vallejo， L. E.， Lobo-Guerrero， S. & Chik， Z. Fractals in Engineering （Springer-Verlag， 2005）.

[6] Andreas G， Gu Y I， Jun K B， et al. Fractal Profit Landscape of the Stock Market[J]. PLoS ONE， 2012， 7（4）： e33960.

[7] Shao Z G， Ditlevsen P D.Contrasting scaling properties of interglacial and glacial climates[J]. Nature Communications， 2016， 7： 10951.

[8] Wu K K S， Lahav O， Rees M J.The Large-Scale Smoothness of the Universe[J]. Nature， 1998， 397（6716）： 225-230.

[9] Parent， R. Computer Animation： Algorithms and Techniques （Newnes， 2012）.

[10] Dewdney， A. K. Computer recreations： of fractal mountains， graftal plants and other computer graphics at Pixar. Sci. Am. 1986， 255： 14-20.

[11] 周禮杲. 分形几何学在生物医学中的应用[J]. 国外医学. 生物医学工程分册， 1991， （05）： 249-256.

[12] 郝柏林.混沌与分形[M]. 上海： 上海科学技术出版社， 2015.

[13] 赵健， 雷蕾， 蒲小勤. 分形理论及其在信号处理中的应用[M]. 北京： 清华大学出版社， 2008.

[14] Heymans O， Fissette J， Vico P， et al. Is fractal geometry useful in medicine and biomedical sciences？[J]. Medical Hypotheses， 2000， 54（3）： 360-366.

[15] 黄润生， 黄浩. 混沌及其应用[M]. 武汉： 武汉大学出版社， 1999.

[16] Mandelhrot B B.Fractals and the rebirth of iteration theory[A]. The beauty of fractals[M]. Springer， 1986. 151-160.

[17] Kenneth Falconer， 福尔克纳， 曾文曲. 分形几何： 数学基础及其应用[M]. 人民邮电出版社， 2007.

[18] Falconer K J. Fractal Geometry： Mathematical Foundations and Applications. by K. Falconer[M]. Wiley， 2003.

[19] Yu， KJ， Yuan， QY， Li. C et al. Comparative Study of Chaos Identification Methods for Wind Speed Time Series under Different Environmental Measurement[J]. Ekoloji. 2019， 28（107）： 3499-3503.

[20] Sarkar， CHAUDHURI B B. An efficient differential boxcounting approach to compute fractal dimension of image[J].IEEE Transactions on Systems Man & Cybernetics，1994， 24（1）： 115-120.

[21] Costabal Sahli F， Hurtado D E， Kuhl E . Generating Purkinje networks in the human heart[J]. Journal of Biomechanics， 2015： S0021929015007332.

[22] Sudarshan， V. K. et al. An integrated index for automated detection of infarcted myocardium from cross-sectional echocardiograms using texton-based features （part 1）. Comput. Biol. Med. 2016， 71， 231-240.

[23] Julesz， B. Textons， the elements of texture perception， and their interactions. Nature， 1981， 290： 91-97.

[24] Sudarshan， V. K. et al. An integrated index for automated detection of infarcted myocardium from cross-sectional echocardiograms using texton-based features （part 1）. Comput. Biol. Med. 2016， 71： 231-240.

[25] Yaniv， Y.， Lyashkov， A. E. & Lakatta， E. G. The fractal-like complexity of heart rate variability beyond neurotransmitters and autonomic receptors： signaling intrinsic to sinoatrial node pacemaker cells. Cardiovasc. Pharm. Open Access， 2013， 2： 1-11.

[26] Huikuri H V， M?kikallio T H， Peng C K， et al. Fractal Correlation Properties of R-R Interval Dynamics and Mortality in Patients With Depressed Left Ventricular Function After an Acute Myocardial Infarction[J]. Circulation， 2000， 101（1）： 47-53.

[27] Rangayyan， Oloumi， Nguyen. Fractal analysis of contours of breast masses in mammograms via the power spectra of their signatures[C]//Engineering in Medicine & Biology Society. IEEE， 2010.

[28] Huang Z， Pan J， Chen G， et al. Fractal Analysis of Two- Photon Microscopic Images for Diagnosis of Nasopharyngeal Cancer[J]. Scanning， 2012， 34（6）： 399-403.

[29] Cymberknop L J， Legnani W， Barra J G， et al. Fractal dimension as an index of left ventricular ischaemia： a pilot study[J]. Physiological Measurement， 2013， 34（1）： 83-97.

[30] Hayano K， Yoshida H， Zhu A X， et al. Fractal Analysis of Contrast-Enhanced CT Images to Predict Survival of Patients with Hepatocellular Carcinoma Treated with Sunitinib[J]. Dig Dis Sci， 2014， 59（8）： 1996-2003.

[31] Hayano K， Lee S H， Yoshida H， et al. Fractal analysis of CT perfusion images for evaluation of antiangiogenic treatment and survival in hepatocellular carcinoma[J]. Academic Radiology， 2014， 21（5）： 654-660.

[32] Orchard S， Ammari M， Aranda B， et al. The MIntAct project-IntAct as a common curation platform for 11 molecular interaction databases[J]. Nucleic Acids Research， 2014， 42（D1）： 358-63.

[33] Al-Kadi， O. S. A multiresolution clinical decision support system based on fractal model Design for classification of histological brain tumours. Comput. Med. Imaging Graph. 41， 67-79 （2014）.

[34] 范坤育. 中醫理论中的混沌理论探析[J]. 山东医学高等专科学校学报， 2014， 36（04）： 317-320.

[35] 黄雁南. 分形几何学、分形生理学和人体穴位分布的分形结构[J]. 北京中医药大学学报， 1996， （06）： 34-36.

[36] 汪慧敏. 人体穴位皮肤电的分维研究[J]. 浙江中医学院学报， 1993， （04）： 50.

[37] 徐天成. 混沌内部的隐秩序-经络内涵的另一种解读[J]. 中国针灸， 2015， （02）： 151-154.

[38] 徐天成， 曹佳楠， 王璇， 盧梦叶， 林祺， 王炜桀. 试探使用分形理论实现经络数字化方法与意义[J]. 辽宁中医药大学学报， 2016， 18（07）： 136-141.

[39] 周德生， 刘利娟. 脑藏象理论解析及分形构建探讨[J]. 湖南中医药大学学报， 2018， 38（10）： 1099-1103.

[40] 张季， 钱峻， 董海艳， 王瑞娟， 杨涛. 基于分形理论的中医数字化舌象苔质纹理分析[J]. 中华中医药杂志， 2016， 31（01）： 104-106.

[41] Shah R G， Girardi T， Merz G， et al. Hemodynamic analysis of blood flow in umbilical artery using computational modeling[J]. Placenta， 2017， 57：9.

[42] Thuring A， K?llén K， Br?nnstr?m K J， et al. Doppler Audio Signal Analysis as an Additional Tool in Evaluation of Umbilical Artery Circulation[J]. Ultraschall in der Medizin -European Journal of Ultrasound， 2017， 38（05）： 549-555.

[43] Alfirevic Z， Stampalija T， Gyte GM. Fetal and umbilical Doppler ultrasound in normal pregnancy[J]. Cochrane Database Syst Rev， 2017， 6（1）：CD007529.

[44] J.C. Echeverría， J. álvarez-Ramírez， Pe？A M A ， et al. Fractal and nonlinear changes in the long-term baseline fluctuations of fetal heart rate[J]. Medical Engineering & Physics， 2012， 34（4）： 466-471.

[45] Spilka J， V. Chudá？ek， Koucky M， et al. Using nonlinear features for fetal heart rate classification[J]. Biomedical Signal Processing and Control， 2012， 7（4）： 350-357.

[46] Kara S， Latifoglu F， Güney M. Fractal Analysis of Umbilical Artery Doppler Signals from Normal Pregnant Subject Using Hurst Exponent[C]// Frontiers in the Convergence of Bioscience & Information Technologies. IEEE， 2007： 582- 586.

[47] 吴晓峰， 王威琪， 余建国， 等. 超声多普勒音频信号分形特征研究[J]. 中国生物医学工程学报， 1999（4）： 389-394.

[48] Latifo?lu F， Kara S， Güney M. Determining fractal dimension of umbilical artery Doppler signals using Hurst exponent[J]. Journal of Medical Systems， 2007， 31（6）： 529.

[49] Nakashima Y， Komatsubara J. MULTIFRACTAL ANALYSIS OF SEISMICALLY INDUCED SOFT-SEDIMENT DEFORM–ATION STRUCTURES IMAGED BY X-RAY COMPUTED TOMOGRAPHY[J]. Fractals-complex Geometry Patterns & Scaling in Nature & Society， 2018， 26（01）： 1850018.

[50] Weibel ER. Fractal geometry： a design principle for living organisms. Am J Physiol. 1991; 261（6）： L361-9.