冲击应力对电连接器性能影响的仿真研究

骆燕燕， 武雄伟， 田亚超， 刘旭阳

(1.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300130； 2.河北工业大学 河北省电磁场与电器可靠性重点实验室，天津 300130；3.许继电气股份有限公司，河南 许昌 461000； 4.国网河北省电力有限公司检修分公司，石家庄 050071)

电连接器是器件与器件、组件与组件、系统与系统之间进行电气连接和信号传递的基础元件，广泛应用于航空、航天、国防等军用和民用系统中[1]。航空、航天电连接器及其组件在运输、碰撞、跌落等过程中会遇到不同程度的机械冲击，在冲击的动态条件下，接触件的接触性能是否良好，对电子设备的可靠性有着重要的影响[2-3]。

围绕储存和使用过程中环境应力对电连接器接触性能的影响, 学者们的研究主要包括两个方面：①不同环境应力的影响研究。支宏旭[4]研究了振动频率、幅值、加速度、电流和环境温度等综合环境应力对电连接器电接触特性的影响规律。Sawchyn等[5]研究了机械冲击对电连接器接触可靠性的影响。文献[6-11]分别对航天电连接器在温度应力、振动应力和综合应力作用下的加速寿命试验的理论和方法进行了大量的研究，并对高可靠性的电连接器进行了寿命评估。②理论和方法研究。文献[12-13]用ABAQUS仿真研究振动应力对电连接器接触件微动磨损的影响。龙慧娟[14]利用有限元软件ANSYS求得配合插合状态下连接器接触件间的接触压力，并通过LS-DYNA软件分析了振动应力作用下插针与插孔间的相对运动；Perrinet等[15]利用摩擦能量密度法预测银镀层微动磨损时的电接触持久性。

本文利用ANSYS建立电连接器模型，对某型号航空电连接器进行冲击试验仿真研究，该模型已经过试验结果验证，具有一定的可靠性[16]。并从能量角度分析电连接器接触性能的变化规律。

1 冲击仿真试验

前期研究发现，当峰值加速度≥2 000 m/s2，接触件的相关参数的变化幅度很大。因此，本文进一步仿真研究了接触件的相关参数在2 000～5 000 m/s2峰值加速度下的变化规律。

1.1 电连接器模型

本文选用某公司生产的三针航空电连接器进行仿真研究，航空电连接器实物图、单个接触件模型及简化动力学模型，如图1所示。在实际工作环境中，由于电连接器的种类、安装方式不同，其受到的冲击应力也有很大区别。为简化分析过程，本文选定在垂直轴线方向的冲击条件下建立电连接器的动力学模型，如图1(c)所示[17]。

图1中，插孔与孔座、插针与针座及针座与孔座之间的作用分别可简化成弹性系数为k1，k2及k3的联接，插针与插孔的接触区域A处存在接触压力N和摩擦力F。

由于插针固装于针座中，而插孔嵌套于孔座中，当受到冲击应力作用时，插针与针座可看做一个整体发生运动，而插孔与孔座间的运动则会有差异，因此，建模时，本文设定k2为无限大，而k1为零。

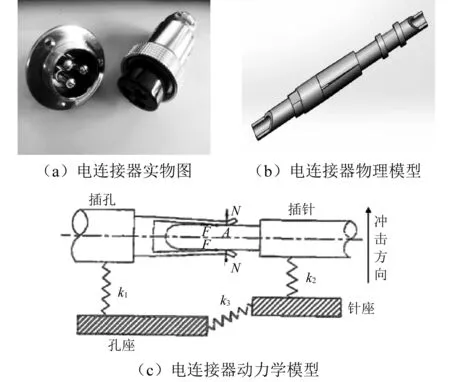
图1 航空电连接器示意图Fig.1 Aviation electrical connector schematic

1.2 方案设计

参照国家标准GB/T 2423.5—1995中应用于各种场合的试验严酷等级和脉冲波形的典型示例以及各个波形特点，本文选用半正弦波脉冲作为冲击脉冲，选择沿插孔到插针的垂直轴向方向作为冲击方向，冲击次数设定为1次；并结合试验研究需要制定不同的冲击试验严酷等级，如表1所示。冲击试验的严酷等级包括脉冲峰值加速度p和脉冲持续时间D，本文用(p,D)来表达。

表1 冲击试验的严酷等级条件Tab.1 Severity levels of shock test

1.3 仿真参数设置

仿真参数的设置包括：依照表2设置接触件材料属性；接触类型设为摩擦接触；接触行为设为非对称接触；接触件主体采用自动网格划分方式，各插孔簧片及接触棱线进行了细密划分，网格单元大小分别设定为1.5 mm和0.15 mm；将插针和插孔固定端分别施加固定约束。接触件的静力学仿真结果如表3所示。

继续添加加速度载荷可得动力学仿真结果。加速度载荷通过分量的方式施加。半正弦波则是通过函数方式施加的，设置关于时间的正弦函数Zsin(At)，通过改变参数Z来得到不同的脉冲峰值加速度p，通过参数t来设置相应的脉冲持续时间D，根据设置好的脉冲持续时间调整系数A来得到该正弦函数的前半周期，这个正弦函数的前半周期波形即为所需波形。

表2 某型号航空电连接器接触件材料属性Tab.2 Material properties of contact parts of a certain type of aviation electrical connector

表3 静力学仿真结果Tab.3 Statics simulation results

2 仿真试验结果

2.1 最大形变量的仿真结果

随着试验严酷等级的变化，接触件的最大形变量的变化如图2所示。

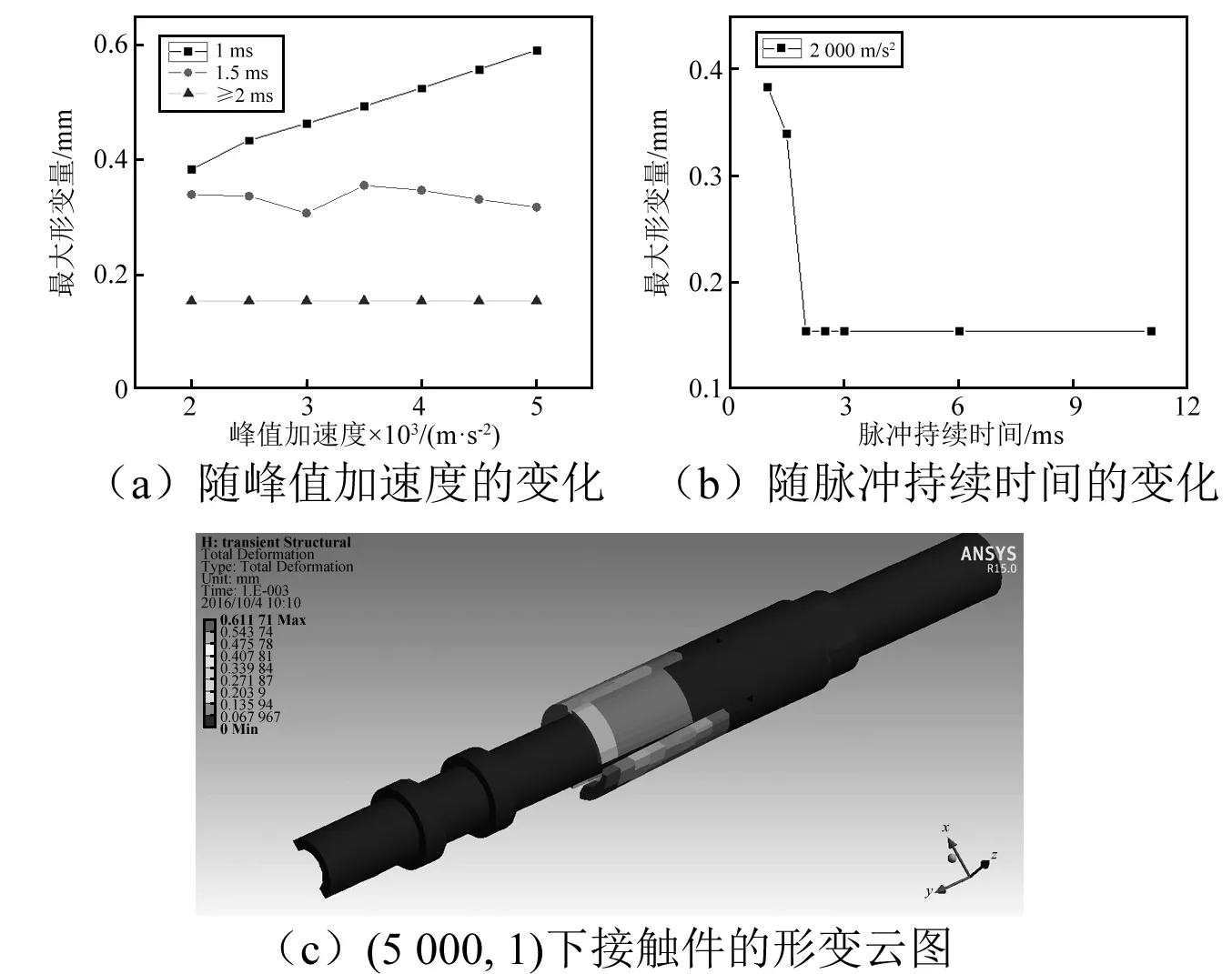
图2 不同严酷等级下最大形变量的仿真结果Fig.2 Simulation results of the maximum deformation under different severity levels

由图2可知：①随峰值加速度的增加，接触件的最大形变量的变化规律与脉冲持续时间有关。1 ms时，最大形变量呈线性增加；1.5 ms时，呈现微小波动；≥2 ms时，几乎保持恒定且与静力学仿真中的形变值基本相同。②峰值加速度相同时，随脉冲持续时间的增大，最大形变量呈现“快速下降后趋于平稳”的规律。在1～2 ms时，最大形变量减小幅度显著，约减小61.25%；≥2 ms后，与静力学仿真结果基本相同。③图2(c)中显示，在严酷等级(5 000，1)时，插孔簧片的端部与插针发生了分离。

由此可见，脉冲持续时间越短，对最大形变量的影响越显著；形变量大幅增加会影响接触件间的紧密插合，使接触压力降低，导致接触电阻显著增加，接触性能退化。由此可推测，脉冲持续时间为1 ms时，出现接触不良现象的概率最高；≥2 ms时，最大形变量几乎可恢复至受冲击前的状态。

2.2 最大应力值的仿真结果

接触件的最大应力值随冲击试验严酷等级的变化如图3所示。

由图3可知：①脉冲持续时间相同时(除1.5 ms外)，随峰值加速度增加，最大应力值基本保持不变，1 ms时，接触件的最大应力值远远大于材料的屈服强度，由此推测会产生局部塑性形变。1.5 ms时，最大应力值先保持平稳，当峰值加速度≥3 500 m/s2后开始逐渐减小。②峰值加速度相同时，随脉冲持续时间的增大，最大应力值先骤减至最小值后缓慢增大，最后与静力学仿真结果保持一致；2 ms是最大应力值变化趋势发生转折的脉冲持续时间拐点。

相比于峰值加速度，脉冲持续时间对最大应力的影响更为显著。

图3 不同严酷等级下最大应力值的变化Fig.3 Changes in the maximum stress values under different severity levels

2.3 接触压力的仿真结果

图4～图6所示为不同严酷等级下接触压力的变化。

由图4可知:①脉冲持续时间相同时，随峰值加速度增加，接触压力极差基本保持不变。②峰值加速度相同时，随脉冲持续时间的增加，接触压力的极差值近似呈“L”形规律减小，最后接近于零；1 ms时，接触压力的极差值远远大于其它脉冲时间下的数值。

由图5可知，接触压力最小值随脉冲持续时间的增加，整体呈“类抛物线”规律增大(除1.0 ms外)；1.0 ms时，接触压力最小值要远低于其它脉冲持续时间下的数值。

由此可知，接触压力仅受脉冲持续时间的影响，且较短的脉冲持续时间会引发接触压力出现明显的波动。

依据电接触理论，接触压力值直接影响电连接器的重要性能指标-接触电阻的大小

Rj=k(0.102F)-m

(1)

式中：F为接触压力，N;Rj为接触电阻，Ω;k为接触材料表面情况等决定的相关系数;m为与接触面形式相关的指数。本文选定接触件接触形式为线接触(m=0.7)；黄铜-黄铜接触(k=670)[18-19]。

由式(1)可知，接触压力越小，接触电阻越大，接触性能退化越严重；而接触压力波动越大，接触性能越不稳定。由图6可知，接触电阻会出现较大波动。

图4 不同严酷等级下接触压力极差的变化Fig.4 Variation of contact force at different severity levels

图5 不同严酷等级下接触压力最小值的变化Fig.5 Changes in minimum contact force at different severity levels

图6 (2 000,1)下接触压力的时间历程曲线Fig.6 Contact force-time history curve at severity level(2 000,1)

国军标GJB 1217—2009“电连接器试验方法”中，接触压降大于电源电动势的50%且持续时间超过1 μs的现象定义为瞬断；本文选定的电连接器试品的接触电阻超过5 mΩ时，即被认为接触失效[20-25]。因此，根据式(1)求出电连接器发生失效时，接触压力的临界值为0.555 N。图6中接触压力小于临界值的持续时间超过了1 μs，由此推断，冲击的初期，接触压力的剧烈波动可能会引起电连接器的瞬断失效。

3 仿真结果中冲击能量分析

3.1 接触形式的分析

接触可分为持续接触和碰撞。物体相互接触，不发生穿透并维持一段时间，这种现象被称为持续接触；而碰撞是用来描述物体在碰撞过程中其速度发生瞬时变化的现象[26]。接触件插针部分为铜合金，可视为圆柱刚体；插孔由弹性簧片组成，前端部分为缩口结构，且缩口半径通常比插针半径小。由此可知，冲击仿真试验中电连接器接触件之间为接触碰撞形式。

3.2 冲击碰撞的能量分析

冲击碰撞过程的实质是能量转化的过程，是将冲击能量转化成内能、热能以及其它形式的能量。

接触件受到冲击作用后获得冲击能量，可假设插针、插孔为接触碰撞系统，并吸收冲击能量。由能量守恒定理可知，在忽略少量能量损失的前提下，冲击能量与系统吸收能量相等。

接触件插孔由金属弹性簧片组成，是有效的吸能结构，能在有限的压缩、变形空间内产生形变而吸收大量的能量。在冲击瞬间，伴随着能量瞬间转化，冲击损耗的动能E主要转变为以下两部分：材料的内能(塑性变形能Ep、弹性变形能Ee)和热能Eo。

接触件系统所接收的冲击能量是通过冲击过程中脉冲速度变化量计算得到的。半正弦冲击脉冲速度变化量计算方法如图7所示。

首先，对冲击脉冲曲线进行整形，在各峰之间取中点连成一条平滑的曲线，整形后曲线所围面积等于原脉冲曲线所围面积。为精确计算速度变化量，需对整形后的曲线从脉冲前的0.4 Th到脉冲后的0.1 Th进行积分。在10%的脉冲高度处划定脉宽，所得曲线更接近于半正弦波，因此速度变化量可近似为[27]

(2)

式中:A为峰值加速度,m/s2;D为脉冲持续时间,ms。

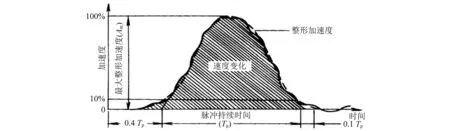
图7 半正弦速度变化量Fig.7 Half-sine rate of change

由式(2)可得不同试验条件下的速度变化量，将式(2)的结果代入动能表达式中

(3)

可得接触件系统吸收的能量为

(4)

由式(4)可知，冲击能量由脉冲持续时间和峰值加速度共同决定，呈正比关系。根据表1设计的试验方案，部分严酷等级下的冲击能量如表4所示。

表4 不同冲击严酷等级下冲击能量Tab.4 Impact energy under different impact severity levels

3.3 仿真结果的能量分析

图8分析了脉冲持续时间1 ms和2 ms、峰值加速度2 000～5 000 m/s2下，接触件相关参数变化与冲击能量变化之间的关联性。

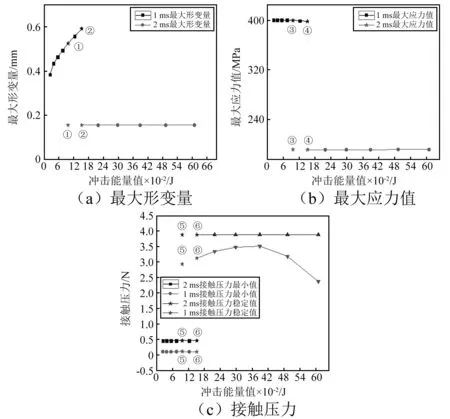
“☆”-相同能量值下接触件相关参数值图8 不同冲击能量下接触件相关参数的变化Fig.8 Variation of some parameters under different impact energies

由图8(a)可知：脉冲持续时间为1 ms时，随着冲击能量的增加，接触件的最大形变量线性增大，且变化幅度较大；2 ms时最大形变量保持不变。

由图8(b)可知：脉冲持续时间为1 ms和2 ms时，随冲击能量的增加，应力值均基本保持恒定；但前者稳定在400 MPa，远远超出接触件材料的屈服强度，可推测会产生局部塑性形变。

由图 9(c)知:脉冲持续时间为1 ms时，随冲击能量的增加，接触压力稳定值呈“先线性缓慢增加、后快速下降”的规律；而最小值则保持基本恒定。脉冲持续时间为2 ms时，接触压力稳定值和最小值均保持基本恒定；且其数值均大于1 ms时的值。

由图8中①～⑥组数据可见，具有相同的冲击能量值的不同冲击严酷等级下，接触件的相关参数值存在差异；脉冲持续时间1 ms时，接触件的相关参数值的变化量较大。这说明，冲击能量的作用效果的强弱主要取决于冲击的作用时间，时间越短，效果越明显。

根据能量守恒定理可知，随着试验严酷等级的增高，施加的冲击能量值增大，接触件系统接收的冲击能也增加；部分冲击能转化的接触件系统的内能也增加。

图9 应力分布云图Fig.9 Stress distribution cloud

脉冲持续时间不同时,内能增加的表现形式存在一定的差异：

①当脉冲持续时间为1 ms时，内能的增加体现在因接触簧片端部的最大形变量的增大(图8(a)1 ms时的曲线)而储存的弹性势能；同时伴随着簧片根部塑性变形区域的些许扩大而吸收的能量，区域中心的最大应力值均超过材料屈服强度，但不随能量的增加而增大(见图8(b)1 ms时的曲线；图9(a)和图9(b))。由于冲击时间短，冲击能量吸收的内能主要以弹性势能为主；冲击消失后，弹性势能释放，簧片端部变形消失，接触压力趋于平稳；但在冲击初期，因簧片变形量大引起接触压力大幅波动(见图6)，存在接触压力过低导致瞬断失效的潜在风险。

②当脉冲持续时间超过2 ms时，接触簧片端部最大形变量基本保持恒定，与静力学分析值相近；内能的增加主要体现在簧片塑性变形区域的扩大(见图9(c)和图9(d))；虽然最大应力值未超过屈服强度，但随吸收能量的增加，塑性变形区域的增大，最终接触件接触压力有缓慢减低的趋势(见图8(c))。

③冲击能量相同的情况下，冲击时间长短不同，导致弹性势能和塑性变形区域吸收的能量的占比有差异，最终使接触件相关参数的变化不同，尤其对接触压力的影响最为明显(见图9(b)和图9(d)，图8(c))。

由此推测，相比于冲击能量数值的高低，冲击施加的时间长短，对接触件相关参数及接触性能的影响更显著。

4 结 论

(1)相比于峰值加速度，机械冲击的脉冲持续时间对电连接器接触件最大形变量、最大应力值和接触压力的影响更为显著；且以脉冲持续时间2 ms为“拐点”，接触件相关参数变化出现明显差异。

(2)电连接器接触压力的波动程度随脉冲持续时间的增加而减小，最小值随脉冲持续时间的增加而增大；与其它脉冲时间相比，1.0 ms时，接触压力值的波动最严重，最小值最低，接触性能最差；冲击的初期，接触压力的剧烈波动可能会引起电连接器的瞬断失效。

(3)从能量分析的角度，冲击能量的增加，不一定会使接触件相关参数发生变化；而冲击的作用时间不同，接触件吸收冲击能量的方式不同，即弹性势能和塑性变形区域吸收的能量占比不同，导致接触件相关参数的变化存在显著差异。