丰富双向细目表，实现初中数学课堂教学减负增效的研究综述

柳月明 许文倩

【摘   要】本文从丰富双向细目表出发，谈了设置更合理的双向细目表，以让教师明晰考试的方向，编制合理的教案，实施减负增效的课堂。另一方面也让学生明白知识点的难易度、考试的题型、分值的比例等，使学生对考试了然于心，避免增加不必要的负担，以达到师生共同减负增效。

【关键词】双向细目表;课业负担;减负增效

一、相关概念界定

1.双向细目表

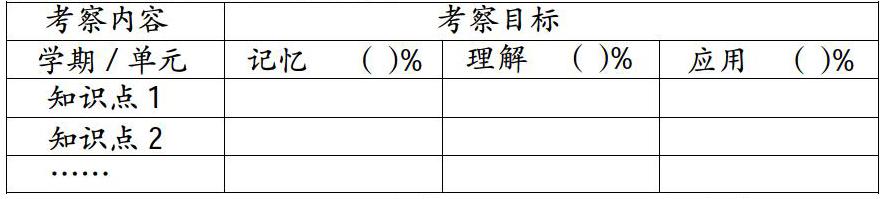
命题双向细目表，主要是参照美国著名教育心理学家布鲁姆关于认识领域里教育目标分类体系，结合本学科的具体特点，由任课教师或专家共同研究确定。命题双向细目表一般由三个要素组成：第一，考查目标，亦称考查能力层次。它具体回答了考试是“考什么”的问题，也体现了该门课程对学生应具备的具体能力的要求。第二，考查内容，亦称考查的知识块。它反映了考试的基本素材，即反映了课程的基本纲要或内容体系。第三，考查目标与考查内容的比例，亦称权重。它反映了考查目标和考查内容各项目之间的相对重要性。命题双向细目表是在具体命题时的主要依据，当然，命题测试又是评价课堂教学效果的主要指标，因此，命题双向细目表对平时的课堂教学有很大的指导性。但是课堂教学有其自身的特点，因此对命题双向细目表要进行丰富。

2.课业负担

课业负担是指课时过多，作业量过大，考试频繁，资料泛滥，各种学科竞赛接二连三，奥校奥班竞相攀比等，是中学教育中比较普遍存在的现象。课业负担是指学生在学习过程中所承担的各种任务，是造成学生学习压力的主要原因。研究发现，学习负担轻重存在这样的现象：学习负担重却生活负担轻，智育负担重却德育负担轻，记忆负担重却思维负担轻。就智育领域而言，学习负担的表现是记忆负担重而思维负担轻，学习量的负担重而质的负担轻。课堂教学中，教师起指导作用，指导学生怎么学习新知识，怎么巩固旧知识，因此，学生的课业负担与教师的课堂教学有很大的关联。

3.减负增效

减负是把过重的不必要的负担——那些会严重损害幼嫩的未成年学生身心健康的超额负担减掉。而不是把学生的所有课业负担都减掉。学习新知识，培养能力，对绝大多数学习者来说，总是存在负担的。负担减下来了，而学习效果反而增加了，这就是所谓减负增效。

二、重负担原因探究

1.知识层面

一是知识量多。就苏州市初中数学中考毕业暨升学考试来说，在知识技能的考试中，数与代数有62个知识点，圖形与几何有100个知识点，统计与概率有15个知识点，合起来共有177个知识点。其中每个知识点中还有2-5个小点。所以知识总量很多。二是知识枯燥。在这些知识点中，有一部分知识很是枯燥。例如，分式的混合运算，生活中用到的不多，对于初二学生来说很是枯燥。三是知识深奥。数学知识大多是抽象出来的，所以有许多知识比较深奥。例如，函数概念，许多学生都是一知半解，很难真正理解。这些都会导致学生学习负担加重。

2.作业量

一是作业量多。因为知识量多，对应的作业量必然多，有时为了巩固所学知识，有的要加以反复，使得作业量翻倍式增多。二是作业难度增加。为了增加学习的深度，教师往往会提高作业的难度，像一些星号题、进阶题、附加题等，增加题目的难度无疑会增加学生的负担。

3.方法

学生在学习中的方法掌握不到位，也会增加学习负担。一是上课走神，有一份问卷调查，460名被调查者中，有128人上课开始后20分钟就开始走神，占27.8%。二是厌恶作业，有115人认为做作业就是受罪，占25%。三是听课不会做笔记，有198人只习惯于听讲，占43%。这些同学在年级的表现通常是成绩在后、学习负担重的同学。究其原因是没有掌握好的、适合的学习方法。

4.考试

考试包含毕业考试和升学考试，也包含了平时的单元考试。一般来讲，毕业考试和升学考试都是基于标准进行命题，其考试的题目、题量都是比较科学的。但是平时的考试，教师往往凭经验编制试卷，甚至随意挑选题目组合成试卷。事实上，教师选用的测试题题目也大多不是评价专门机构或专业人员开发、编制的。这会导致考试的难度、知识比例、题量等方面的随意性，从而增加学习负担。

三、对策研究

1.知识与方法

一是注重数学知识的结构化。把知识点串成知识线，把知识线结成知识网，让学生从整体上认知知识，把握整体，明白某一知识点在知识体系中的位置、价值等。例如，近几年苏州市教科院注重每一章的章头课的研究（苏州市开创了一个先例），笔者曾经试上了一堂分式的章头课。我是这样设计的，实际问题（行程问题）引出数学模型，有分数有分式，回顾分数的运算及其性质，猜想分式的运算及其性质，指出可能的学习方向，导出了以后每一堂课所要研究的具体内容。在小结时，我是这样处理的：

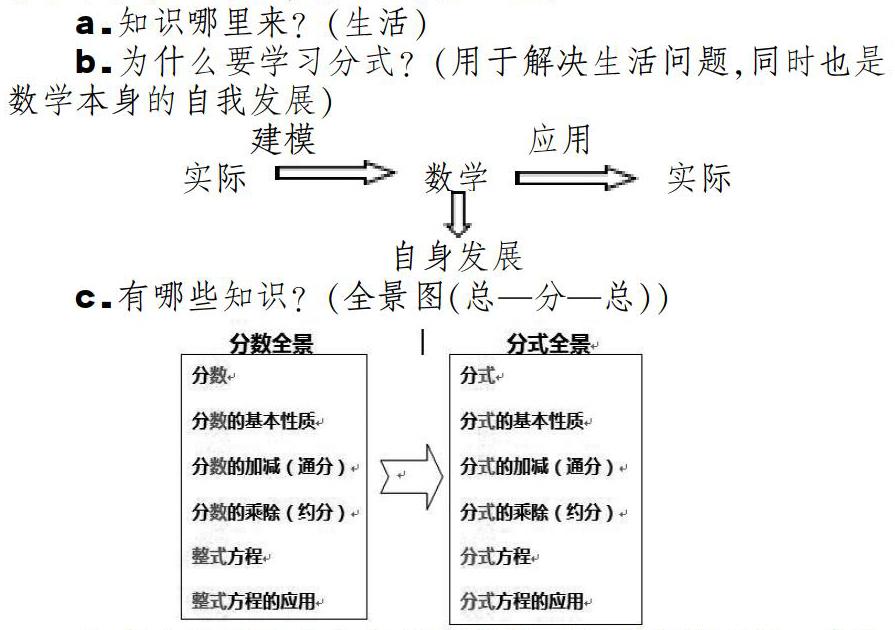
a.知识哪里来？（生活）

b.为什么要学习分式？（用于解决生活问题，同时也是数学本身的自我发展）

c.有哪些知识？（全景图（总—分—总））

d.怎么学习分式的内容？（类比，“管中窥豹可见一斑”，但是要防止“瞎子摸象”的现象，因此要总体把握知识结构。）

e.分数与分式在形式上可以统一成：。

这样，学生的学习能通顺、能贯通，因此能学得扎实。

二是注重数学知识的顺序化。数学知识是一根链条，一环连一环，因此，在知识的学习上必须注意前后联系，注意因果关系，弄清楚先后顺序。例如，几何上的论证，用前面的定理可以证明后面的结论，否则会成为循环论证。

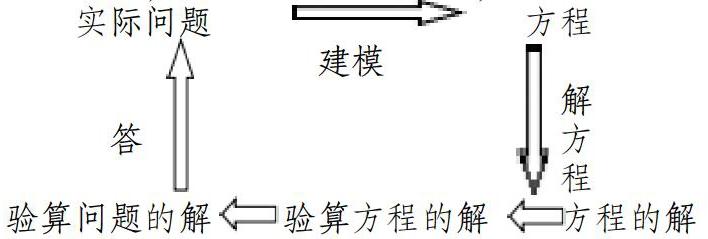
三是注重数学知识的系统化。知识导图就是一个很好的方法。例如，初一的一元一次方程，这一章的系统就是：

这样，学生对一元一次方程的知识就能系统掌握。

2.作业与考试

对于作业的设计，一是题量上要加以控制，课内弄清了，课外的巩固性的题目可以很少甚至不再布置。二是难度上要加以限制，把难题以小题目的形式逐渐加深，就是低进入，人人可进，高走出，能够走出来就是高手。