基于回归分析的河流弯曲度影响因素研究

金天昊 丁少玲

【摘 要】本文主要研究影响河流弯曲度的主要因素。从河流长度对河流弯曲度的影响出发，进行相关性检验、线性拟合等，在去除异常值点并完成检验后得出线性方程。随后对河流源头的纬度和弯曲度的关系进行研究，在将纬度划分区域后发现一些与假设不同的结果。

【关键词】回归模型;相关;河流弯曲度;经纬度

中图分类号： O212.1;P343.1 文献标识码： A 文章编号： 2095-2457（2019）24-0131-002

DOI：10.19694/j.cnki.issn2095-2457.2019.24.061

0 引言

（1）研究背景

河流形态，是河流呈现出来的直观的形态。充分理解河流的形态我们可以更好的了解河流对于生态环境的重要作用及其与包括经济社会等多个方面人类活动的潜在联系。

弯曲度是指具有至少一个拐点的曲线长度和欧几里得距离的比值。该值的范围从1到无穷大[1]。在对河流的研究中，河道弯曲度是指河道长度与河谷长度之比。在具体的河流中，直接下坡流动的基岩流的弯曲度指数为1，蜿蜒的河流的弯曲度指數大于1[2]。

（2）研究历史及现状

1996年科学家Hans-Henrick Stolum[3]，计算了从河流源头到出河口的实际距离与它们的直接距离的比值。并猜想比例近似等于3.14，即π。Stolum认为河湾演化呈现出一种自组织过程，并将河流形态分为混沌状态和有序状态。上述研究说明河流弯曲度是可以不断变化由各种因素的影响处于动态的平衡之中，但论文中并没有给出具体的影响因素包括哪些。李志威等[4]利用线性或非线性统计的方法以大量河湾为样本，统计弯曲度变化区间，并发现冲积河湾的弯曲度均值和标准方差都大于山区河湾。且天然河湾的横向相对偏移度与弯曲度成较好的线性关系。

1 本文的研究方法以及数据介绍

本文方法主要使用线性回归模型，易于解释本文数据的问题。数据包括地球上278条河流的名称、长度、源头及结尾处经纬度和弯曲度等。来自英国数学家James Grime的网站（PiMeARiver.com）。数据处理部分使用SPSS Statistics 22.0软件处理。

对本文数据做简单的数据处理时发现在所有得到的数据之中计算出的河流弯曲度平均值较小于3.14，大约为1.92。

2 河流长度与弯曲度

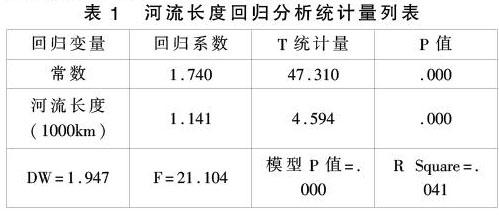
本文首先选择河流长度与因变量，探究河流长度与河流弯曲度之间是否有联系。此处河流的单位为千米。确定变量间的相关性。由软件运行得到相关性表得知，斯皮尔曼相关系数为0.398为中等程度的相关。

拟合结果说明通过参数显著性检验，由ANOVA表可知，模型通过显著性检验SPSS输出Durbin-Watson检验结果为1.947，接近2满足具有相互独立的观测值的假设。

通过残差与回归拟合值或标准化残差与标准化预测值之间的散点图进行检验。所以认为回归符合等方差的基本假设。从而可以确定模型的基本假设是满足的。

最终，在完成正态分布假设检验后建立模型，通过系数表和ANOVA表（整合如下）说明该模型的系数检验和模型检验均可以通过。模型效果良好。

河流弯曲度和河流长度的简单线性回归的模型为

y=1.740+1.141x

其中y为河流弯曲度，x为河流长度，单位为1000千米。这表明河流长度与河流弯曲度有着相关性，当弯曲度和河流长度在大致同一取值区间之内时，可建立较为直观的简单线性方程。该方程可解释为，每当河流长度增加1000千米时，河流的弯曲度增加1.141。诚然，河流改变1000千米是一个很大的改变量，但是在全部河流弯曲度的范围只有 [0.116，5.88]的情况下变化量1.141已经是较大的变化。

对于河流长度和河流弯曲度这两个变量来说。在做出非线性尝试拟合后，发现有的拟合模型效果不好，这里不做详细的描述

3 河流纬度与弯曲度

3.1 初步的相关分析与回归

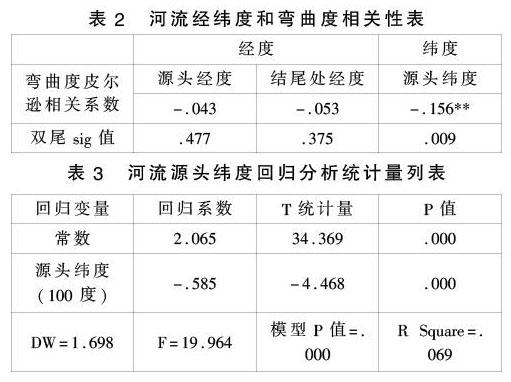
在详细研究河流长度和弯曲度的关系之后本文转而研究弯曲度与河流经纬度的关系，数据包含河流源头经纬度，河流结尾处经纬度。本文着重以河流源头处的经纬度为代表河流大致经纬度。首先在对河流源头处和结尾处的经度分别与因变量河流弯曲度进行相关性分析时，发现经度对河流弯曲度的影响效果并不大。

这和我们经验相符，河流的东西朝向不会影响河流的蜿蜒程度。而河流的南北纬度的分布可能会受地转偏向力的影响。所以我们着重研究以纬度作为自变量对河流弯曲度的影响。本文以河流源头的纬度为代表进行分析。

上表发现河流源头纬度与河流弯曲度呈现程度一般的相关性，检验是显著的，于是以河流源头纬度代替河流大致纬度进一步研究其与河流弯曲度的关系。

为了直观的表示线性方程，将河流源头的纬度数据化单位为100度。按照相似的线性拟合过程进行处理，在去除异常值点后得到拟合结果说明通过参数显著性检验且通过模型显著性检验。

SPSS输出Durbin-Watson检验结果为1.698，很越接近2满足具有相互独立的观测值的假设。回归残差近似正态分布假设可以由标准化残差的直方图确定（此处省略）而且从正态P-P图看出各点分布离对角线很近，说明数据越接近于正态分布。散点图残差点不同拟合值对应的残差应大致相同分布，所以认为回归符合等方差的基本假设。

最终河流弯曲度和河流源头纬度的简单线性回归的模型为

y=2.065-0.858x

其中y为河流弯曲度，x为河流源头纬度（包含正和负），单位为100度。综合考虑河流源头纬度确实与河流弯曲度有一定的相关性，每当河流源头纬度增加100度时，河流的弯曲度减少0.868，考虑地球纬度分为南纬和北纬数值均在0至90度之间。将南纬作为负值后，总体范围只有180度所以纬度变化100度对河流弯曲度的影响0.868变化效果不大。

3.2 进一步的考虑：纬度的分类

考虑可能的影响因素是地球自转产生的地转偏向力。地转偏向力，是一种惯性力，是对旋转体系中进行直线运动的质点由于惯性相对于旋转体系产生的直线运动的偏移的一种描述。地转偏向力因其性质在极地最显著，向赤道方向逐渐减弱直到消失在赤道处。因此可以将纬度数据进行分类处理，研究其在不同纬度地区的影响是否出现差别。

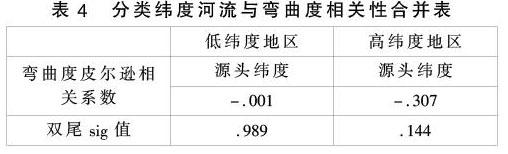
由于南半球的数据量少，本文对北半球的数据进行分类处理，按照通常的纬度分类以0-30度作为低纬度地区，30-60度为中纬度地区，60度以上为高纬度地区，现实中高纬度地区的河流很少，所以本文将中纬度地区和高纬度地区数据合并，以北纬30度为界限分为低纬度地区河流和中高纬度地区河流，分别对纬度变量和河流弯曲度进行相关性分析，得出下列结果。

由表格看出低纬度地区河流的相关性为-0.307相比于中高纬度地區河流的相关性（-0.001）差距很大，从现有知识并不能解释为什么会发生这种现象，从地理角度出发，很可能与地转偏向力有关。

4 结论

在对本文数据做简单的数据处理时发现地球科学家Hans-Henrick Stolum[5]发表论文之中所猜想的河流弯曲度比例近似等于3.14，即圆周率π在实际的河流数据中并没有准确的表现，相反的，在所以得到的数据之中计算出的河流弯曲度平均值较小，大约为1.92。针对河流长度对河流弯曲度的影响进行分析时，由相关性表得知，斯皮尔曼相关系数为0.398为中等程度的相关。长度确实对河流弯曲度有影响。在完成多项假设检验后得出线性方程y=1.740+1.141x。该方程可解释为，每当河流长度增加1000千米时，河流的弯曲度增加1.141。

当把河流的纬度作为自变量进行分析时，发现河流纬度与弯曲度有不强的负相关性却依然显著，得到河流弯曲度和河流源头纬度的简单线性回归的模型为y=2.065-0.858x。并发现与经度不同，河流分布的纬度不同可能会使河流受到不同的地转偏向力的影响，由地转偏向力的性质出发，将河流源流出纬度分为低纬度和中高纬度进行分别的分析。发现低纬度地区河流的相关性为-0.307相比于中高纬度地区河流的相关性（-0.001）差距很大。

【参考文献】

[1]Leopold L B， Wolman M G， Miller J P. Fluvial processes    in geomorphology[M].Courier Corporation，2012.

[2]Mueller J E. An introduction to the hydraulic and topographic sinuosity indexes[J].Annals of the Association of American Geographers，1968，58（2）：371-385.

[3]St？覬lum H H. River meandering as a self-organization process[J].Science， 1996， 271（5256）： 1710-1713.

[4]李志威，秦小华，方春明.天然河湾几何形态统计分析[J].水科学进展，2011，22（5）：638-644.