Multi-parameter optimization of machining impeller surface based on the on-machine measuring technique

Gng WANG, Wen-long LI,*, Fn RAO, Zheng-rong HE, Zhou-ping YIN

a State Key Laboratory of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan 430074, China

b China National South Aviation Industry Co., Ltd, Zhuzhou 412002, China

KEYWORDS

Abstract Selecting the optimal machining parameters for impeller surface is a challenging task in the automatic manufacturing industry,due to its free-form surface and deep-crooked flow channel.Existing experimental methods require lots of machining experiments and off-line tests,which may lead to high machining cost and low efficiency. This paper proposes a novel method of machining parameters optimization for an impeller based on the on-machine measuring technique. The absolute average error and standard deviation of the measured points are used to define the grey relational grade for reconstructing the objective function, and the complex problem of multi-objective optimization is simplified into a problem of single-objective optimization. Then, by comparing the values of the defined grey relational grade in a designed orthogonal experiment, the optimal combination of the machining parameters is obtained. The experiment-solving process of the objective function corresponds to the minimization of the used errors,which is advantageous to reducing the machining error. The proposed method is efficient and low-cost, since it does not require re-clamping the workpiece for off-line tests.Its effectiveness is verified by an on-machine inspection experiment of the impeller blade.

1. Introduction

The impeller is one of the most important parts in an aircraft engine. It is mainly composed of several blades attached around an axial hub, and used to compress the working gas for generating flight power.A small deviation in the geometric shape of the impeller surface may lead to a large degradation of its operation performance. Due to the free-form surface structure and the deep-crooked flow channel of the blades,usually a 5-axis machine tool with a high length-diameter ratio(LDR) is used to cut the material of a workpiece. In practice,one common problem encountered in machining is that a high LDR may result in continuous cutting vibration for a toolworkpiece system, and this vibration may be further enlarged by the un-optimizable selections of the depth of cut and feed rate.How to select the optimal parameters of the LDR,depth of the cut, and feed rate plays a critical role in improving the machining quality and operation performance of an impeller.

Many efforts have been devoted to mathematical modeling and parameter optimization for machining complex parts,such as free-form surface parts or thin-walled parts. Pyo1proposed a modeling and calculation method to determine the machining strategies and the optimal machining conditions for impeller blades. Ming et al.2deduced a mathematical expression of the residual height of abrasive grains and built a model of grinding surface roughness for machining parameters optimization of face gear surface.Guo,et al.3introduced a plate dynamic model to predict the vibration characteristics of thin-walled parts, and this model was used to decouple the workpiece vibration resulting from machining process parameters (spindle speed and part thickness). Liu, et al.4proposed an interim feature modeling and machining parameters optimization method for aircraft structural parts, and Gok et al.5presented a modeling method for selecting the optimal parameters of the cutting speed, feed rate, and tool path style when machining parts in aircraft, aerospace, and automobile industries.Hou et al.6modeled the milling forces of a worn tool and presented a novel recognition method of milling tool wear. It can be used to optimize the cutting conditions and tool type.In addition, some researchers7-10investigated a genetic algorithm-based method for machining parameters optimization, and simulation/real experiments were carried out to test the proposed method’s effects.

Over the past two decades, many experimental methods have also been developed for machining parameters optimization. Wang and Jianu11developed a smart sensing unit for vibration measurement and machining parameters adjustment,and conducted experiments to demonstrate its feasibility and validity.Karandikar et al.12proposed a grid-based experimental design method to identify the process damping coefficient in milling, and experimental results showed that it could significantly reduce the number of traditional experimental design methods, such as the factorial design and response surface methodology.Astakhov and Galitsky13experimentally investigated the combined influence of the cutting speed, feed rate,approach angles, flank angles, and vertical shifts of cutting edges on the drilling tool life. It was found that the adjustments of the design parameters could improve the maximum tool life and drilling feed. In addition, Puertas, Tzeng, and Secilmis respectively proposed14,15different experimental methods to select the machining parameters of electrical discharge machining (EDM), where the surface roughness and material removal weight were observed and analyzed.Recently,research of machining parameter optimization based on the Taguchi strategy16-18is very active.Usually,an orthogonal experiment is designed to acquire observation data. In practice,for multi-parameter optimization of impeller machining, it should overcome two critical problems: (1) LDR selection. One important feature in impeller machining is to use a high LDR parameter for avoiding the interference, especially for machining the flow channel regions. However, a high LDR parameter may lead to uncontrollable cutting vibration,which increases the machining error of the impeller surface;(2)cost and efficiency. A common method of experientially obtaining the optimal machining parameters is to carry out lots of machining experiments and off-line test experiments(such as a roughness test).It has to bear the drawbacks of high machining cost from expensive materials/machine tool operation and inefficiency waiting from off-line tests.

In recent years, an automatic on-machine measuring technique with a touch probe or a laser scanner has begun to find extensive applications.19-21Since the measuring sensor is integrated into the machine tool,it can directly measure the workpiece shape and evaluate its machining error without reclamping the workpiece for off-line tests. In our previous work,22measuring accessibility cones have been defined to generate a continuous interference-free probing path. It can efficiently evaluate the machining error of an impeller’s surface by the on-machine measuring technique.In this paper,the onmachine measuring technique is further used to resolve the task of multi-parameter optimization for impeller machining.The absolute average error and standard deviation between the on-machine measured points and the design surface are used to construct an objective function, which includes three machining parameters: length-diameter ratio, depth of cut,and feed rate. Then, the grey relational grade (GRG) of each measuring experiment is defined and used to reconstruct the objective function, which changes the task of multi-objective optimization into a task of single-objective optimization. By maximizing the defined GRG in the reconstructed objective function, it can obtain the optimal machining parameters.The main merits include:(1)this method simplifies the calculation process from multi-objective optimization to singleobjective optimization, and it can simply compare the GRG value for analyzing the machining quality;(2)this method uses the absolute average error and standard deviation to define the GRG for reconstructing the objective function, and it can experimentally calculate the optimized LDR parameter by maximizing the GRG value. It is noteworthy that the maximization of the GRG corresponds to the minimization of the used errors, which is advantageous to reducing the machining error;(3)this process is efficient and low-cost,since it does not require re-clamping the workpiece for off-line tests. The used orthogonal array has the advantages of uniform neat comparable, thus the number of experiments is small, and machining/verification experiments for obtaining the optimal parameters can be implemented only in one workblank. In practice,orthogonal experiments should be carried out on experimental samples. Through the analysis of experimental results, the optimal horizontal combination of processing parameters of this part is obtained, and then the optimized process parameters could be applied to the subsequent actual products.

The remainder of the paper is organized as follows.In Section 2,the objective function for multi-parameter optimization is defined. In Section 3, orthogonal experimental design and on-machine measurement are introduced. In Sections 4 and 5, the calculation process of optimizing machining parameters and experimental result analysis are presented, respectively.Conclusions are given in Section 6.

2. Objective function of machining parameter optimization

The purpose of optimizing machining parameters is to improve the machining quality of the impeller surface.Define the objective function as

For free-form surfaces,the absolute average error and standard deviation are used to evaluate the machining quality.Thus, the functions in Eq. (1) are defined as

where AE X( ) is the absolute average error, SD X( )is the standard deviation, ek，k=1，2，...，r is the distance deviation between the ith measured point and its corresponding closest point in the design surface, andis the mean value of ek.

AE X( ) reflects the overall machining error of a blade. A high AE X( ) indicates a low machining precision. SD X( )reflects the dispersion degree of the measurement error distribution of the blade. A high SD X( ) indicates that the machining errors in different regions change greatly. This means that the blade may be partially deformed,or may be locally abnormal due to processing vibration.These two objective functions respectively reflect the machining precision from the aspects of deviation size and dispersion degree of the deviation distribution, so they can reflect machining quality comprehensively.

The impeller surface is designed with a free-form and thinwalled structure, and its flow channel is deeply crooked. Usually,a milling tool with a high LDR is used to cut the material.However, it encounters a universal problem that a high LDR enlarges the possibility of cutting vibration for a toolworkpiece system. Although a low LDR is beneficial to restraining the vibration, it enlarges the possibility of collision and interference. In practice, how to select a suitable LDR parameter is an important task for machining quality.In addition,the selections of cutting parameters,mainly including the depth of cut and the feed rate,also play a vital role in machining quality.In the following,the LDR,depth of cut a,and feed rate f are defined as the machining parameters required to be optimized, and Eq. (1) changes into

Note that the cut-and-try method with experiential data is a common method to select the machining parameters in Eq.(3).However,the cost is very high since lots of experiments have to be implemented to obtain enough observation data. The optimal combination of the machining parameters varies with different operators and machining conditions. In the following,the Taguchi-based grey relational analysis23will be used to reconstruct the objective function of machining parameters in Eq. (3) On one hand, the used orthogonal experimental array has the advantages of uniform neat comparable, which can greatly reduce the time and cost of the orthogonal experiment. On the other hand,the GRG processes and normalizes the raw data to fit between zero and one, which can translate the problem of multi-objective optimization into a problem of single-objective optimization.

The closer the absolute average error and standard deviation in Eq. (2) are to zero, the better the quality of blade processing is. This is the lower-the-better performance characteristic. The loss function can be expressed as

where l=1，2，...，s is the procedure of repeated experiments,Lj，mis the loss function of the jth objective function in the mth experiment, and fj，mX( ) is the experiment value. Taguchi recommended the use of the loss function to measure the performance characteristic deviating from the desired value. The loss function can be further transformed into a signal-tonoise (S/N) ratio as follows:

where yj，mis the S/N ratio for the jth objective function in the mth experiment, and it is expressed in dB units.

In the Taguchi method,the S/N ratio is used to evaluate the deviation of the performance characteristic from the desired value.This is because the S/N ratio can reflect both the average and the variation of the quality characteristic. When the optimization objectives fj，mX( ) in Eq. (4) are approximately 0, the S/N ratio is higher.This means that the higher the S/N ratio is,the quality of blade processing is. Through an analysis of the S/N ratio of experimental results,we can find out the relatively optimal parameters horizontal combination with strong antiinterference ability,good adjustment ability,and stable performance,so as to improve product quality.It is observed that in Eq.(5), the highest value of yj，mis expected when selecting the machining parameters. However, for different f1，m，f2，m，...，fq，m, the optimal machining parameters X are not consistent. To deal with this problem, the normalized S/N ratio zj，mis defined as

Then, the grey relational coefficient ξj，mfor the jth objective function in the mth experiment is

The GRG is a mean value of the grey relational coefficient in Eq. (7). It is defined as

where γmis the GRG in the mth experiment. Note that the greater the value of GRG in Eq. (8) is, the smaller the values of the absolute mean error and standard deviation are, which correspond to a low machining error. Therefore, the objective function in Eq. further changes into

where the GRG γ is the objective function, and LDR，a，f are the machining parameters required to be optimized. It can be seen that the problem of multi-objective optimization (AE and SD) in Eq. (3) is transformed into the problem of singleobjective optimization (γ) in Eq. (9) The GRG analysis can take both the absolute average error and standard deviation into consideration, so as to obtain the relatively optimal parameters horizontal combination that can optimize the comprehensive effect of the two optimization objectives.

3. Orthogonal experimental design and on-machine measurement

Table 1 Machining parameters in the L9 34orthogonal array.

Fig. 1 Layout of the measuring procedure of an impeller.

For each blade, the iso-parametric method is used to generate the measured points of the pressure surface, leading edge, and suction surface for three measuring paths. In Fig. 2., 35 measured points are respectively placed on the suction and pressure surfaces, and 10 measured points are placed at the leading edge for each path. The generated paths are simulated in PowerInspect for interference checking, and input into an NC system (Heidenhain iTNC530M)for real touching operation. In Fig. 3, the touch probe system used is Renishaw OMP40, and its repeated accuracy is 1 μm in touching directions. The obtained distance deviations between measured points and the design model of three blades are shown in Fig. 4. It is observed that the distance deviations, which reflect the machining errors of the blades, are all within 0.15 mm. The distance deviations on the suction surface are almost positive (undercut), and the distance deviations on the pressure surface are almost negative (overcut). It is also observed that the distance deviations in the first path are relatively larger than those in the other two paths. The main reason is that the blade is designed with a thin-walled structure (poor rigidity), and machining transformation is sensitive to the cutting force especially in the top regions of the blade.

Fig. 2 Three measuring paths generation for a blade of the impeller.

Fig. 3 Real touching process of both suction and pressure surfaces for a blade.

4. Calculation and solution of optimizing multiple parameters

4.1. Step 1: calculation of the S/N ratio

The distance deviations for each blade are used to calculate the absolute average error (AE) and standard deviation (SD) by using Eq.(2).Then,Eqs.(4)and(5)are further used to calculate the S/N ratios of the AE and SD, respectively. Calculated results are shown in Table 2.

4.2. Step 2: calculation of the GRG

To obtain the required optimization parameters,the operation of a normalized S/N ratio is carried out by Eq. (6),and calculated results are shown in Table 3. Then, Eqs. (7) and (8) are used to calculate the grey relational coefficients and grades,respectively. Calculated results are shown in Table 4. Since the experimental design is orthogonal, it can separate out the effect of each machining parameter at different levels.According to experimental results in Table 4, the mean GRGs of the LDR at levels 1, 2, and 3 can be calculated by averaging the GRG values for experiments 1-3, 4-6, and 7-9, respectively.The mean GRGs of a,f at levels 1,2,and 3 can also be calculated according to the corresponding GRG values. Table 5 shows calculated mean GRGs and max-min values, the maximum mean GRGs minus the minimum mean GRGs at levels 1,2,and 3,and Fig.5 displays the response rule of the machining parameter at levels 1, 2, and 3.

As mentioned earlier,it is the lower-the-better performance characteristic for the defined absolute average error and standard deviation. In this situation, it corresponds to the highest value of the mean GRG in Fig. 5. Therefore, the optimal machining parameters for the objective function Max γ( LDR，a，f) in Eq. (9) are LDR1a1f2in the experiments.

4.3. Step 3: variance analysis and F-test

The purpose of the variance analysis is to investigate the significance of the three machining parameters. Firstly, the total sum of the squared deviations SSTfrom the mean value of the GRGs is calculated by

Fig. 4 Distance deviations between measured points and the design surface in three paths.

Table 2 S/N ratios of 9 experiments with respect to those in Table 1.

Table 3 Normalized S/N ratios with respect to those in Table 2.

Table 4 Grey relational coefficients and grades with respect to those in Table 3.

where t=9 is the number of experiments in the orthogonal array, andis the mean value of each γm. Note that the value of SSTis composed of the following four parts:

Meanwhile, there exists

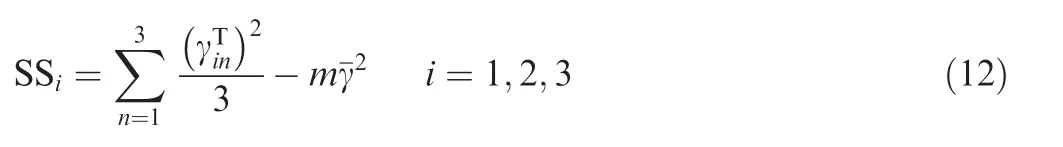
Table 5 Mean GRG and max-min analysis, where the value of the total mean will be used to carry out a variance analysis in Section 4.3.

Fig. 5 Mean GRGs for distance deviations.

The F-value of the ith parameter is

Correspondingly, the contribution of the ith parameter is

where Si=SSi-DiVe.Calculated results are shown in Table 6.According to the F-test method,24in the experiments, if 9 ≤Fi＜19, it is generally significant; if 19 ≤F ＜99, it is highly significant; if F ≥99, it is extremely significant. It can be seen that the order of the significance is LDR ＞a ＞f.According to the results of the variance analysis, the LDR is extremely significant with F=453.8. The main reason is that the impeller blade is designed with a free-form surface and a deep-crooked flow channel, and usually tools with a high LDR are used to cut the material. It may result in continuous cutting vibration which enlarges the distance deviation, which is greatly affected by the value of the LDR.

5.Experiment verification and analysis of the optimal machining parameters

When the optimal combination LDR1a1f2of the machining parameters is determined in Section 4, it can further predict and verify the improvement of the performance characteristic.The predicted S/N ratio at the optimal level is calculated by

Table 7 Prediction and comparison results.

It can be seen that the predicted S/N ratios are basically equivalent to the experimental ones: 26.8522 vs 27.5082 and 33.6834 vs 33.4161.It is also observed that the defined distance deviations(AE and SD)of the 10th blade are smaller than the mean values of the 1-9th blades in the orthogonal array. The improved percentages are 18.1%and 22.8%,respectively.Correspondingly, the S/N ratios of the 10th blade are also improved when compared with those of the mean values of the 1-9th blades. It is verified that the proposed multiparameter optimization method is effective, and it can find the optimal combination of machining parameters in experiments, which can reduce the distance deviation and improve the machining accuracy.

6. Conclusions

This paper addresses the problem of machining parameters optimization for impeller surface. The on-machine measuring technique is used to acquire the distance deviations between measured points and the design surface. The GRGs from the distance deviations are calculated and compared to obtain the optimal machining parameters, including the LDR, depth of cut,and feed rate.The major advantages include the following: (1) it simplifies the calculation process from multiobjective optimization to single-objective optimization; (2) it can experimentally calculate the optimized LDR parameter,which is very important to restrain the cutting vibration in impeller machining;(3)it is efficient and low-cost,since it does not require re-clamping the workpiece for off-line tests and avoids lots of expensive materials and machining cost. In the verification experiment using the optimal machining parameters,the absolute average error and standard deviation directly responding to the machining error are reduced by 18.1% and 22.8%, respectively.

It should be noted that the level of the optimization factors is set as 3 and the number of the orthogonal experimental design is set as 9,in consideration of saving experimental time and cost. Without loss of generality, if the level and the number of the designed orthogonal experiment are increased, the proposed method can obtain better machining parameters.

Acknowledgments

This work was co-supported by the National Basic Research Program of China(No.2015CB057304)and the National Natural Science Foundation of China (Nos. 51535004 and 91648111).