An intelligent algorithm for coherent sound source localization based on a strong tracking filter

Jincho JI, Ling WANG, Mingxin WANG, Song FU

a School of Aerospace Engineering, Tsinghua University, Beijing 100084, China

b Department of Mechanical Engineering, Army Aviation Institute, Beijing 101123, China

KEYWORDS

Abstract Background noise is inevitable when sensor arrays are used for aeroacoustic measurements in wind tunnels.The direct removal of background noise,however,would affect the measurement accuracy. In particular, the existing array signal processing algorithms are either invalid or inefficient for removing the noise that is coherent with the signal of interest.In this paper,an intelligent algorithm is developed to localize the coherent sound sources and background noise in real time by iteratively checking the collected data from the array.The proposed method can automatically adjust the suboptimal fading factor to extract useful information as much as possible in residual sequence. This algorithm is tested in simulations and then demonstrated in an experiment.Compared to the two existing methods, the results indicate that the new method has a good phase-shift tracking ability and rapid estimation-error convergence speed, and can achieve an acceptable performance even for low-cost acoustic sensors. Overall, the proposed method should assist array beamforming and hence benefit aeroacoustic measurement.

1. Introduction

In aeroacoustic measurements, models produce a series of complex signal sources. Both signal-generated area identification and signal-intensity quantification play key roles on the consequent noise-reduction application.1,2In recent years,acoustic sensor arrays become a commonly-used and reliable noise testing tool.3-5Unfortunately, the acquisition data of the array is a mixture of signal and background noise, with the former usually weaker than the latter, which should be entirely removed.6

To date,there exists no suitable signal processing algorithm for general acoustic sensors to address this issue.The Classical Beamforming (CB),7based on the assumption of incoherence between background noise and signal of interest, uses Cross Spectral Matrix (CSM) subtraction to remove background noise. An Extended Kalman Filter (EKF) was designed to delete coherent background noise,8,9but its convergence speed is not fast enough, and the empirical constant cannot be adjusted in real time according to the phase shift of the background noise. In order to obtain higher resolution, the array diameter and channels are increasing,10,11the performanceprice ratio should be weighed in the selection of acoustic sensors. However, the price of current instrument-level acoustic sensors is 3-4 orders of magnitude higher than that of lowcost acoustic sensors, which restricts their applications.12For measurements, although some researchers have already proposed special installation methods to reduce the boundary layer noise,13,14the phase shift of low-cost acoustic sensors is inevitable in certain frequency bands,which should be considered in the experiment.

The objective of this work is thus to develop an intelligent algorithm for low-cost acoustic sensors,to quickly remove the coherent background noise with the existence of phase noise,as well as accurately print out the sound-source state in real time for different phase shift.

This paper is organized as follows. Section 2 presents an array-data acquisition model and combines it with the Strong Tracking Filter(STF)theory,15,16then an intelligent algorithm based on STF is developed. It is evaluated in both numerical simulations and an experiment,as presented in Section 3.Conclusions of this work are given in Section 4. The two algorithms for comparison in this study, are briefly introduced in Appendix.

2. Formulations

2.1. Array-data acquisition model

Starting from the simultaneous acquisition of sound pressure by all acoustic sensors,the acquisition time series T are divided into lots of data blocks of length T|k.The output of the acoustic sensor is yn, n=1，2，...，N, where N represents the number of acoustic sensors. Suppose that there appears a point-sound source xSin the wind tunnel at a certain time t,from the quasisteady point of view, ynand xSare related by a complex constant of proportionality for each acoustic sensor Gn=e-iωσ(xn，xS)/D(xn，xS), where Gnstands for the propagation factor, σ(xn，xS) and D(xn，xS) the propagation time and propagation distance from the point source xSto the acoustic sensor position xn, respectively. Since the same Gnis applied for every block, random variations in xSare exactly tracked by the narrowband acoustic sensor signals yn.17

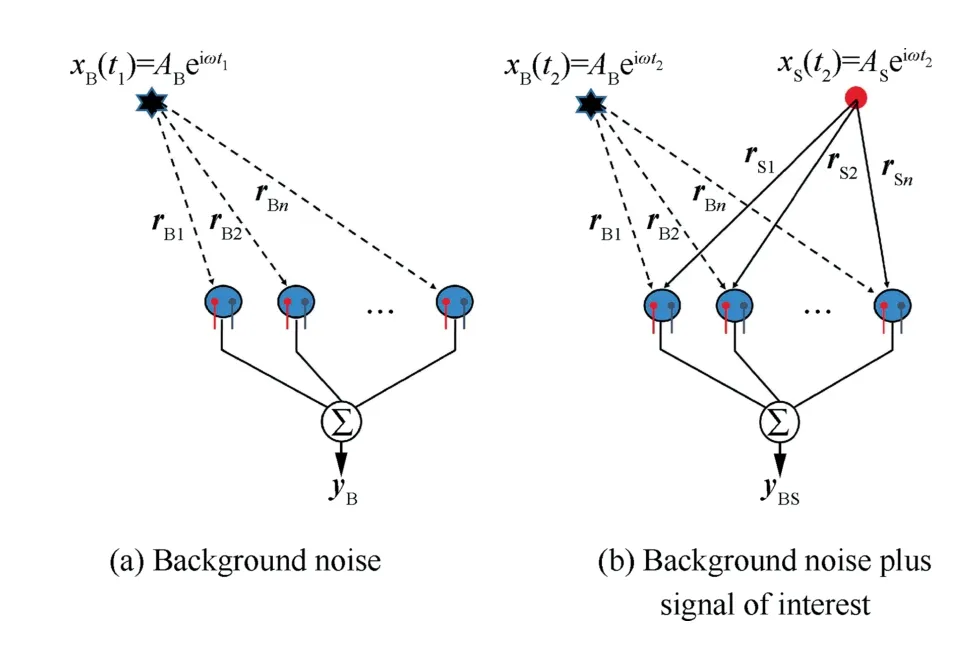
Fig. 1 Array-data acquisition models.

The frame work of array-data acquisition models are depicted in Fig. 1, in which A is the amplitude of the sound source and r ∈RN×1the distance between the sound source and the acoustic sensors. The wind tunnel background noise xB(t1) is measured before a model installed (see Fig. 1(a)),the output of the array is yB. Then, a model is placed in the wind tunnel,as shown in Fig.1(b),the array collects the signal of interest xS(t2) and the background noise xB(t2) synchronously, the output yBScontains both the signal and the background noise.Note that there is a certain phase difference between the background noises in two measurements, the corresponding emitted time are t1and t2,respectively. Due to the time-varying environment of the wind tunnel, the changes of the model, and the phase noise of the acoustic sensors, the phase difference between the two background noises is not an exact value and phase shift presumably occur in the measurement process. Therefore, it is necessary to accurately estimate the phase shift of background noise, then using the background noise xB(t1) to remove the phase-changed background noise xB(t2),finally,we can localize the coherent sound source xS(t2).

The measurement for the two scenarios described above has the form as below to considerably include background noise interference

where y ∈RN×1is the output of the array, G the propagation vector, x ∈R1a single source, and the integral represents the sound source distribution area, calculated by overlaying the grid points of the scanning plane, the subscripts B and S stand for the background noise and the signal of interest,respectively. φ is the phase shift, further written as φ=φ0+φ′+ω(φ). Here φ0is the initial phase difference between the two measurements of the background noises; φ′represents the potential phase shift caused by wind tunnel flow,model or acoustic sensors.For the steady state,φ′should be 0,but it may have a sudden change during the acoustic measurements; ω(φ) is assumed to be normally distributed with mean 0 and variance R, then E［ω(φ)］=0,

E［ω(φm)ωT(φn)］=R(φ)δ(m，n).

2.2. Intelligent algorithm design

Accurate estimation of the time-varying nonlinear phase shift φ in Eq.(1)can help us to quickly release the coherence restriction between the signal of interest and the background noise.Here, an adaptive state-estimation method based on a Strong Tracking Filter (STF)15,16with the least-square algorithm, is developed to address this issue. STF is derived from EKF to extract useful information from the residual as much as possible. It satisfies the following formulations

where the superscripts^and T denote the state estimation and the vector transpose,respectively, and γ the residual sequence.Eq. (3) is called the orthogonality principle, whose physical meaning is that the residual error sequence should be made mutually orthogonal at each step,and it makes the filter robust to the uncertainty of the model.Ref.18shows that the residual of EKF is a non-autocorrelated Gaussian white-noise sequence when the model accurately matches the system,that is,Eq.(3)does not weaken the EKF capability. Both formulations (2)and (3) work as objective functions of STF.

The discrete-time controlled process of the array measurement can be described in the frequency domain as

where A is the state-transition matrix, X ∈C1and Y ∈CN×1the Fourier transforms of the time domain signals x and y,respectively. The signals collected by an array are almost stationary and ergodic during the acquisition process, so that A in Eq. (4) can be regarded as an identity matrix.19Note that in Eq. (4) there exist three variables XB|k, XS|k, and φ|k. The first two are linear while the third is nonlinear. For nonlinear cases,φ|k=φ0|k+φ′|k+ω(φ)|k,with all the factors in Eq.(1)considered here. Particularly, we rewrite the nonlinear system for φ|kas

From Eqs.(6) and(7),we derive the phase-shift estimation of the kth data block,. Here, a suboptimal fading factor Λ|k+1is introduced into the estimate error covariance of EKF,20then we obtain the time-update equations as

Moreover, the measurement-update equations satisfy

Once the STF algorithm achieves a quite accurate phaseshift estimation, we have16

where Sij|k=S|k, N is the number of acoustic sensors, and M the grid points of the scanning plane. Then, we chose the suboptimal fading factor Λ|k+1that corresponds to the minimum of g|k+1. Λ|k+1can be approximately calculated based on Eq.(1) (see Ref.16in details):

where

Here, tr is the trace of a matrix, N|k+1=V0|k+1-R|k+1,M|k+1=H|k+1A|kPk|kAT|kH*|k+1, V0|k+1can be calculated as

where the forgetting factor ρ of 0.95 satisfies 0 ＜ρ ≤1.

Here gives a brief summary of the intelligent algorithm establishment.First,based on Ref.9,a system of the nonlinear state φ|kis refined,where we consider three variables φ0|k,φ′|kand ω(φ)|k, that dominate the nonlinear state. Second, useful information is extracted from a residual sequence γ|k+1: (A)solve Eqs. (17), (18), and (19) to obtain the suboptimal fading factor; (B) adapt a suitable gain matrix K|k+1in real time for fast convergence of estimation error, making γ|k+1(approximately) orthogonal to each other, i.e. the residual sequence behaves like white noise. Finally, localize the coherent sound source xS: solve Eq. (13) to update the phase-shift estimation and to filter out the coherent background noise with recursive operations.

Table 1 Phase settings of 175 data blocks.

Fig. 2 Comparisons between present and EKF algorithms.

3. Results & discussion

The results presented here correspond to the three algorithms employed in this investigation. Results by CB, EKF, and the present algorithms are labeled CB, EKF, and intelligent,respectively. The present algorithm is first tested in numerical simulations. Two spatially coherent noise sources are positioned 0.5 m above the array plane. The array consists of 32 acoustic sensors. The data acquisition process is the same as that in Fig. 1. Table 1 sets up 175 data blocks for the phase shift of the background noise in two measurements:In the first 100 blocks, the phase changes every 20 blocks, with totally 5 variations; In the next 50 and the last 25 blocks, the phase changes every 10 and 5 ones,respectively.Note that the largest phase shift of 90°, occurs at the 41st, 121st and 161st blocks,respectively.

Fig. 3 Coherent background noise rejection.

Fig.2(a)compares the convergence of the present and EKF algorithms for all blocks. It is seen that the former tracks the variations faster in the whole process.Even the phase-shift varies every 5 blocks(the 151st-175th blocks),better tracking ability is still maintained for the present algorithm,while the phase estimation of EKF algorithm cannot converge until the next phase shift occurs,the tracking ability is seriously deteriorated by the high density phase-shift from the 151st to the 175th blocks. Fig. 2(b) shows the corresponding estimation errors of both the present and EKF algorithms, respectively. The errors of the latter are comparably larger for different phase shift,e.g.the phase shift is 90°at 41st data block,and the error nearly reaches up to 60°. When the phase shift interval becomes shorter(the 151st-175th blocks),the estimation errors of EKF keep at a higher level, while the one of the present algorithm at the 41st data block is only about 30°, for other cases the errors are generally less than 10°.In the steady state,the two algorithms have the same estimation error. Fig. 2(c)presents the suboptimal fading factor Λ response during the process.Λ makes the optimal or suboptimal changes for different phase shift and the changes are tuned in real time automatically without any manual interventions.

Fig. 3 compares the beamforming results for removing coherent background noise of CB,EKF,and the present algorithms at the 41st data block with 90° phase shift. For clarity,the first 40 data-blocks beamforming result for CB, the 40th data-block results for EKF and the present algorithms are also presented.Suppose that the monopole at(0.3,0)is the signal of interest,and the dipole at(0,0)the coherent background noise,both with the frequency of 5 kHz.It can be seen that the detrimental effect caused by the coherent background noise partially retained from the 40 to the 60 blocks in CB results,unrelated to the number of processing data blocks. Due to large phase shift, 8 blocks are needed for EKF algorithm to remove the dipole noise completely, accounts for 40% of the 20 blocks, while using the present algorithm, the coherent background noise is almost removed and the signal of interest is satisfactorily restored with 3 blocks, only takes 15%.

It is worthwhile to emphasize that Fig. 3 only presents the beamforming results of the largest phase shift in the process.For other cases (not shown), with phase shifts of 15°, 30°,and 60°, the coherent background noise cannot be removed only at the phase-shift block for the present algorithm, significantly less than EKF algorithm. In total 175 data blocks, the contamination by coherent background noise is shown in Fig.4.The proportion unable to restore signal of interest takes 9% for the present algorithm, while for EKF algorithm is 31%.

Furthermore,we consider the phase noise ω(φ)that always exists in wind-tunnel measurements. Fig. 5 shows the convergence speed of the phase-shift estimationand the suboptimal fading factor Λ response with different phase noises.The phase shift of background noise is also set to 90°, f=5 kHz, and ω(φ) is supposed to be white, with normal-probability distribution.When the covariance R of ω(φ)takes different values,the tracking results of the present algorithm are almost the same,mainly because Λ is adjusted synchronously with different phase noises.It makes the estimations all trend to be optimal. Moreover, Λ stabilizes as the phase is stable. It confirms the robustness of the present algorithm to phase noises,even in the case of acoustic sensors with Gaussian white phase noise.It expands the application range of low-cost acoustic sensors in experiments.

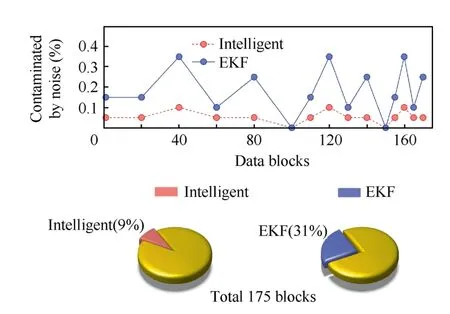
Fig.4 Data blocks contaminated by coherent background noise with different phase shift,a comparison between present and EKF algorithms.

Fig. 5 Present algorithm results with different phase noises.

Fig. 6 Present algorithm results with different frequencies.

Fig. 7 Sound source measurement at LHXY.

Fig. 6 shows the broad-band application and powerful phase-shift tracking capability of the present algorithm. The phase shift of background noise also set to 90°, with only 10 data blocks shown for the magnification details.It is seen that the estimation error converges most quickly at 5 kHz, reaches the minimum value in only 2 data blocks. For other frequencies,the estimation errors converge within 5°in 3 data blocks.Accordingly, Λ response tunes with the phase shift.

Fig. 8 Beamforming result of two speakers by CB (100 blocks).

Fig. 7 presents the experiment setup in LHXY (Army Aviation Institute) Acoustic Laboratory. All the settings remain the same with the simulations, except that the dipole source is replaced by a monopole, due to the difficulties in setting dipole source in the experiment. The array is manufactured on a printed circuit board in a multi-arm spiral with lowcost acoustic sensors. The data acquisition equipment is NI PXIe-1062Q chassis, inserted with the PXIe-8115 real time module and PXIe-4499 data acquisition card. Two speakers driven by the same signal generator produce the spatially coherent sound, the frequency tunes to 5 kHz. The left one is regarded as the background noise,and the right one generates the signal of interest.The distance from the two speakers to the array plane is 0.5 m. First, the left speaker provides the background noise, the array output is YB. The data stream is cut into various blocks, with each block including 4096 samples for the Discrete Fourier Transform (DFT) efficiency. Subsequently, two speakers work simultaneously, with the output YBS. The phase shift between two background noises is set to 120°. Particularly, the coherent background noise is about 3 dB stronger than the signal of interest for mimicking the reality in wind tunnels. The two-speaker beamforming result by CB in 100 data blocks is presented in Fig. 8.

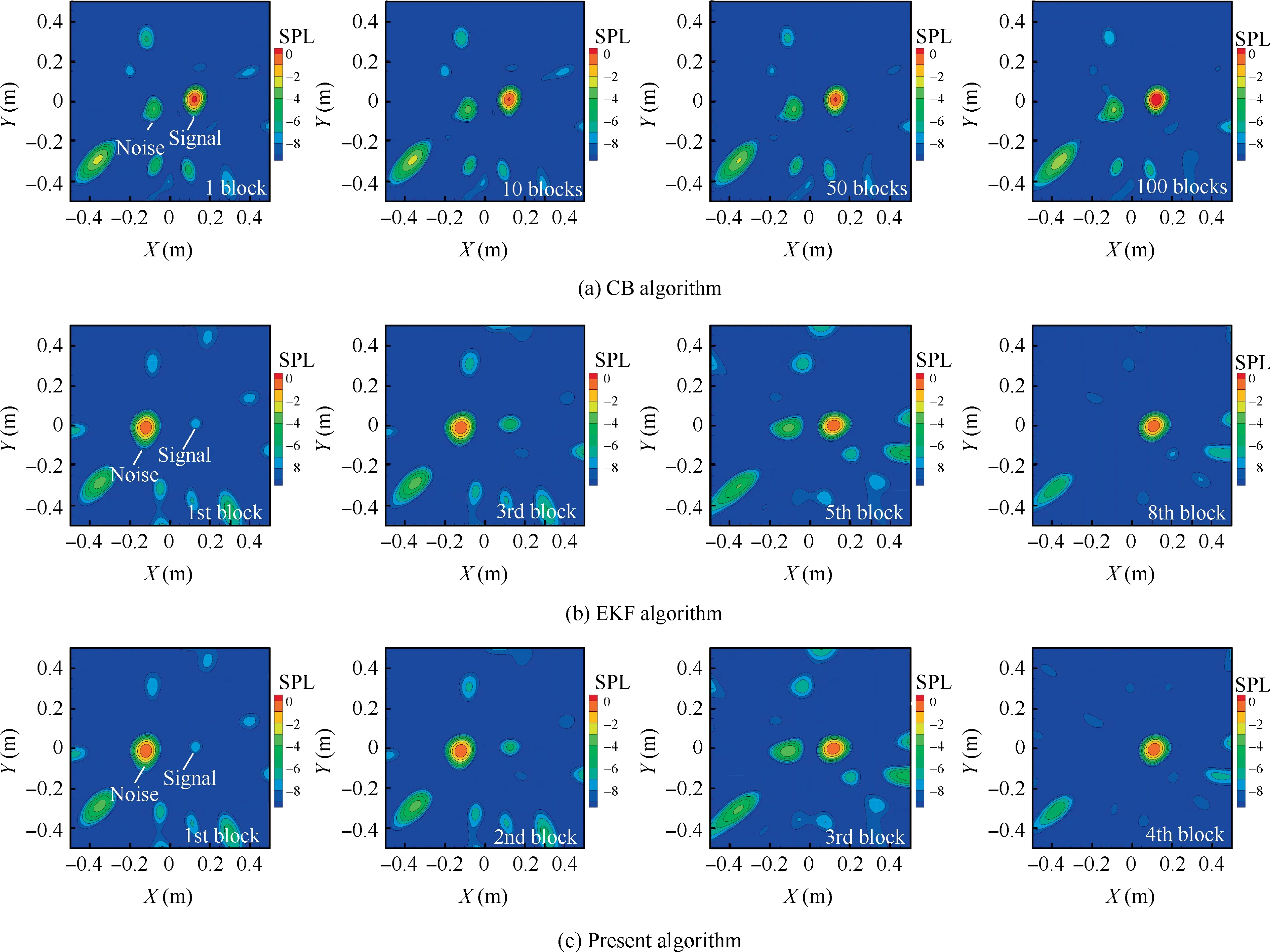
Fig. 9 Coherent sound source identification.

Fig.9 compares the beamforming results by the three algorithms to obtain the signal of interest. It is seen that the noise removal results in 1, 10, 50, and 100 data blocks by CB algorithm, fails to completely remove the interferences of the coherent background noise. EKF and the present results indicate that both algorithms can completely delete the coherent background noise, with 4 blocks needed for the present one while 8 for EKF. Fig. 10 further compares the phase estimation errors of the present and EKF algorithms. The former requires only 3 data blocks, whereas the latter requires 7 data blocks to achieve the accuracy of 5°. It can be concluded that the convergence speed of the present algorithm is much faster than EKF algorithm.

Fig. 10 Estimation errors of present and EKF algorithms.

4. Conclusions

In this paper an intelligent algorithm is developed based on the combination of an array-data acquisition model and the STF theory. This algorithm recursively operates the array collected data and updates the gain matrix in real time to localize coherent sound sources. It adaptively tracks different phase shift and the whole process does not require any manual settings.

The present algorithm is tested both in simulations and in an experiment,in comparison with two existing methods.Note that to increase the test difficulties,dipole source is adopted in the simulations while the source intensity of the noise is set stronger than that of the signal in the experiment. Compared with CB algorithm based on arithmetic average, the present algorithm not only removes the coherent background noise,but also has a potential for real time calculation. It is more robust to the model uncertainties and the phase-shift estimation error converges faster than EKF algorithm.The two algorithms trend to identity in steady states. It illustrates that the coherent background noise with different phase shift can be quickly removed in an optimal way. It is adaptive to lowcost acoustic sensors and applicable in a wide frequency range.Besides, the new approach is carried out in the frequency domain, advanced signal processing techniques can be introduced to further improve the resolution.In all, the fundamental advantages of the present method are manifest both in terms of accuracy and costs in acoustic measurements.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Nos. 11402305 and 11572177), and the Tsinghua University Initiative Scientific Research Program (No.2015Z01014).

Appendix A. CB algorithm

Assuming that the array contains N acoustic sensors,the point sources in the sound source distribution area are noncorrelated and propagate in a spherical wave form, then the acoustic sensor output can be described in the frequency domain

Here, Y ∈CN×1is the output of the acoustic sensors,X ∈C1represents the point source,ω is the angular frequency,τ ∈RN×1is the propagation time of sound source to each acoustic sensor (For simplicity, (iω) is omitted).

For CB algorithm, the phase shift between the two background noises is not considered, that is, φ=0 in Eq. (1), the model can be simplified in frequency domain as

Here, XBS=XB+ XS, due to linearity. The covariance matrices C of the output YBand YBScan be expressed as

where 〈〉 denotes an ensemble average.

The rejection of background noise by CB algorithm is based on the incoherence assumption between the background noise and the signal of interest. That is XBX*S=0, XSX*B=0,then the following result can be obtained

In addition, CB algorithm based on arithmetic averaging fails to deliver real time computational capability,when a large number of channels are adopted in an array,the algorithm has to be conducted offline due to the burden in the Cross Spectral Matrix(CSM)computations,which is computed by averaging over many sampling blocks.

Appendix B. EKF algorithm

The EKF algorithm8is developed in the area of signal processing.The time-domain output y(t)of the array is a column vector consisting of the measured data of N acoustic sensors, the time series y(t) is divided into k data blocks chronologically,DFT is performed on each data block to obtain its spectrum Y|k. For each grid point of the observation plane, the data acquisition equation is

The nonlinear state φ|kcan be estimated by EKF20

This method is limited by the disadvantages of the EKF itself. Generally, EKF is used to estimate time invariant parameters, when the system reaches steady state, K|k+1tends to the minimum in Eq.(B2).20However,there are many uncertainties in the measurements of the wind tunnel, when the phase of background noise φ|k+1is abruptly changed, the residual sequence γ|k+1will increase,but K|k+1does not change accordingly, which results in poor tracking performance. If φ|k+1keeps changing, the algorithm even lose tracking ability.Of course, we can manually adjust the convergence speed by setting different value of m in Eq. (B3), but blindly changing m with the unknown value of φ|k+1may cause the system to diverge.21It is also unreasonable to use the same m for different phase shift and there is no guarantee that the results are always optimal. In addition, if we consider the phase noise ω(φ)in the process,the beamforming result will be even worse.In short, EKF algorithm needs to be further improved to address the aforementioned issue.