基于时空-状态网络的机车调配运用模型与算法研究

姜安培，陈军华，王志美

（北京交通大学 交通运输学院，北京 100044）

机车调配是安排机车牵引列车的过程,是一种复杂的指派问题,即在规定时间内,以机车运用成本最小为目标,完成机车与列车的匹配关系,是铁路运输组织研究的重点之一[1-2]。在机车调配时需要考虑机车的牵引区段是否固定,其中非固定牵引方式允许跨区域牵引列车运行,具有更高的运输效率[3-4]。有些研究从运行图不成对[5]、多机牵引[6]、实时调整[7]等角度对非固定牵引区段的机车调配运用进行探讨,并引入时空网络对机车的运用配置进行优化[8-9]。目前关于机车调配的研究多将机车任务的接续或折返限制在区段站及其以上等级车站,而实际生产组织中中间站也会办理上述作业。为解决该类机车调配问题,提出一种两阶段调配方法,以机车是否需要回段检修为依据划分为2个阶段：第一阶段安排机车牵引接续较为紧密的列车以形成牵引任务组,第二阶段安排机车执行相接续的牵引任务组。通过构建时空-状态网络描述两阶段调配方法流程,将时间、空间和机车的牵引状态等信息整合在网络中,建立非固定区段机车调配的0-1整数规划模型。

1 问题描述

机车调配问题需要解决的是根据线路上的列车运输任务,合理确定牵引机车的来源以及任务完成后的去向。机车在运行时会占用线路上的空间资源,因而调配过程需要通过整合机车对时间与空间的利用情况,以最小成本完成规定的列车牵引任务。先将铁路线路看作一维空间,加入时间轴后即可表示机车在时空网络上的运行情况。而机车自身的时空信息不足以支持调配决策,机车当前是否牵引列车对机车运用会产生直接影响,因而将机车的牵引状态加入到网络中,建立时空-状态网络模型。

1.1 基于时空-状态网络的机车调配过程

基于时空-状态网络的机车调配过程,主要采用两阶段的机车调配方法。

（1）第一阶段在考虑机车牵引状态的基础上,调配机车执行车站间形成的列车接续任务,形成机车不回段的一次牵引任务组。机车的初始状态为0,此时可以前往其他车站或在该站等待后续牵引任务；机车连挂列车后,状态变为1,此时只能执行列车的牵引任务,直至与列车分离,状态变回0。

未进行优化的机车调配时空-状态网络如图1所示,图1中示意了机车a,b和c的牵引任务,T轴表示时间,D轴表示距离,S轴表示状态。设StationA和StationC距离Depot1较近,StationB距离Depot2较近。机车a由Depot1出发前往StationC,在连挂上列车1后,状态由0变为1；将列车运至目的地StationB后,状态变回0,而后返回机务段Depot1。

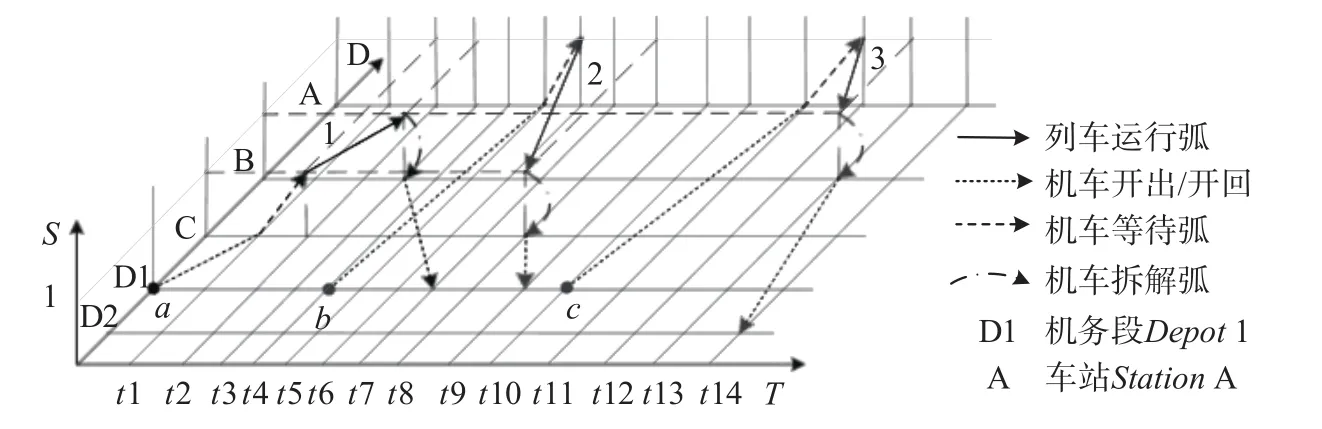
图1 未进行优化的机车调配时空-状态网络Fig.1 Space-time-state network of unoptimized locomotive assignment

该方案为每列车配属1台机车,完成牵引任务后机车返回机务段,机车调配第一阶段的时空网络图如图2所示,为减少空走成本,图2中给出改进。机车a在完成列车1的牵引任务后,由StationB单机前往StationA,而后等待至列车2的发车时刻,牵引其到达StationC,而后由StationC开回与其距离最近的机务段Depot1,至此机车a完成一个牵引任务组,即第一阶段完成。

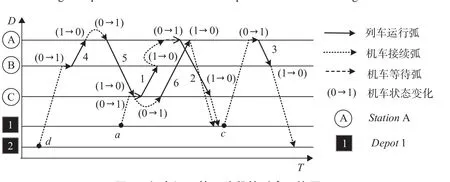
图2 机车调配第一阶段的时空网络图Fig.2 Space-time network of locomotive assignment in phase 1

（2）第二阶段将以同一区段站为起讫点的牵引任务组进行串联。机车调配第二阶段的时空网络图如图3所示,图3中机车k1由Depot3出发,完成牵引任务组a后进行整备,之后继续执行牵引任务组c,而后返回Depot1整备。之后完成任务组g的牵引工作后,机车k1回Depot3,至此得到机车k1的全部牵引任务。

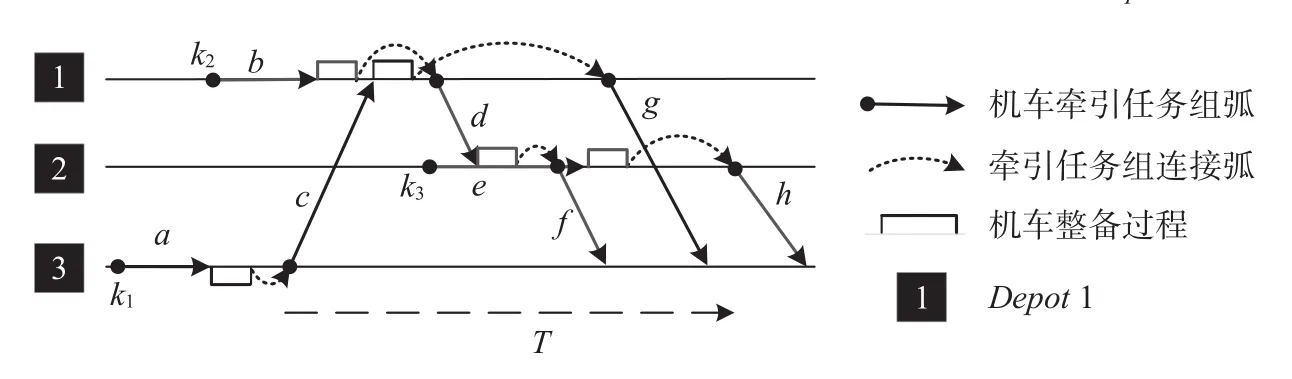
图3 机车调配第二阶段的时空网络图Fig.3 Space-time network of locomotive assignment in phase 2

1.2 重载列车多机牵引求解

由于重载列车需要多机牵引,因而会由于列车种类的不同而产生不同的机车指派方案,采用“影子列车”代替法,将不可由单机牵引的重载列车“分解”为一组多列的普通列车。分解后每组“影子列车”具有完全相同的参数设置(如到发时刻、停靠车站等),但服务同组“影子列车”的机车不必同时到达。

机车调配问题的图形输入如图4所示,每列普通列车在网络中有2个坐标点(departi,arrivei),分别代表起点和目的地；而每列重载列车由多列完全相同的“影子列车”组合而成(如列车5'和5"组成重载列车5)。机车一般由以点表示的机务段(如机务段Depot1)出发,分配到与该机务段邻近的各车站,执行出发列车的牵引任务。

在对列车信息进行初步处理后,通过建立混合整数规划模型,在第一阶段搜索可行方案,得到一系列的牵引任务组,第二阶段给出启发式规则进行机车周转图的铺画,获得机车所执行的牵引任务组,进而确定每台机车的列车牵引任务。

图4 机车调配问题的图形输入Fig.4 Graphical input in locomotive assignment problem

2 基于时空-状态网络的机车调配运用模型

2.1 符号定义

引入3个0-1变量,xijk= 1表示机车k从列车i或机务段i前往列车j或机务段j,xijk= 0表示其他；ypk= 1表示机车k从机务段p出发,0表示其他；ukt= 1表示机车k在t时刻已连挂列车,0表示其他。模型涉及的集合和参数如表1所示。

2.2 模型构建

考虑机车运转时间、保有数量、接续匹配、位置状态和列车时间窗等约束条件,以资源消耗少、机车作业强度均衡、调配连续性强为 目标建立模型如下。

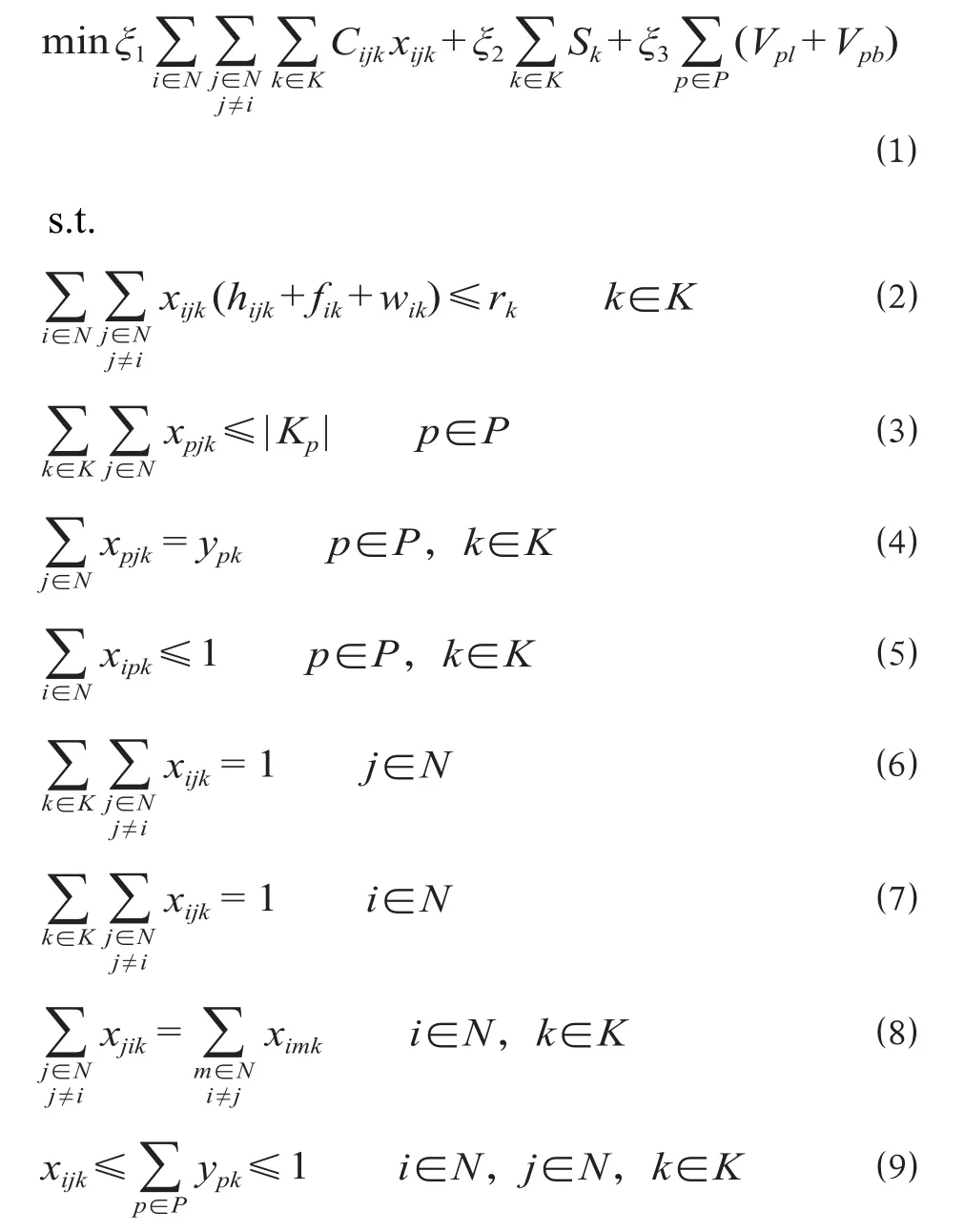
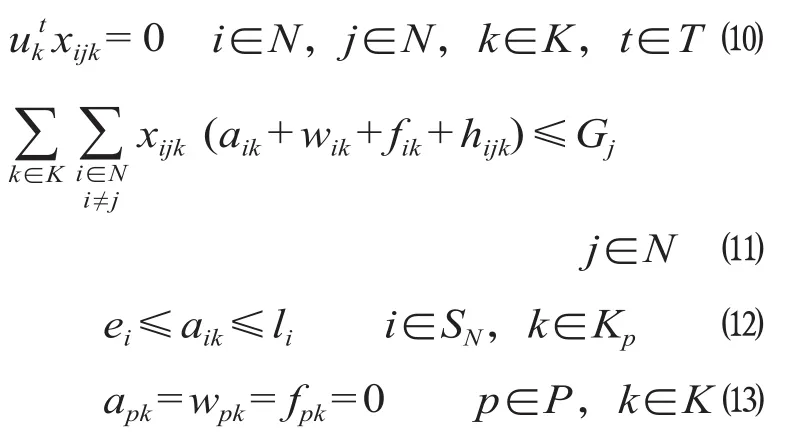
模型的目标函数包括3部分：一是在保证完成列车牵引任务的前提下,机车调配过程中所消耗的资源最少(空走费用,等待费用等)。二是由于每台机车均由机务人员执行任务,并且机务人员排班计划一般以机车运用计划为基础,因而为保证机务人员工作强度的均衡,必须保证调配方案中每台机车在运转时间、运转距离以及等待时间等方面的均衡性。这里引入机车工作时间方差作为目标函数,实现机车工作强度的均衡。三是为保障各机务段服务强度的均衡性和后续调配工作的接续性,加入机务段的开出/驶入机车数量方差作为目标函数,使得各机务段在一定周期内机车进出数量大抵相当。其中ξ1,ξ2,ξ3为目标函数权重系数。

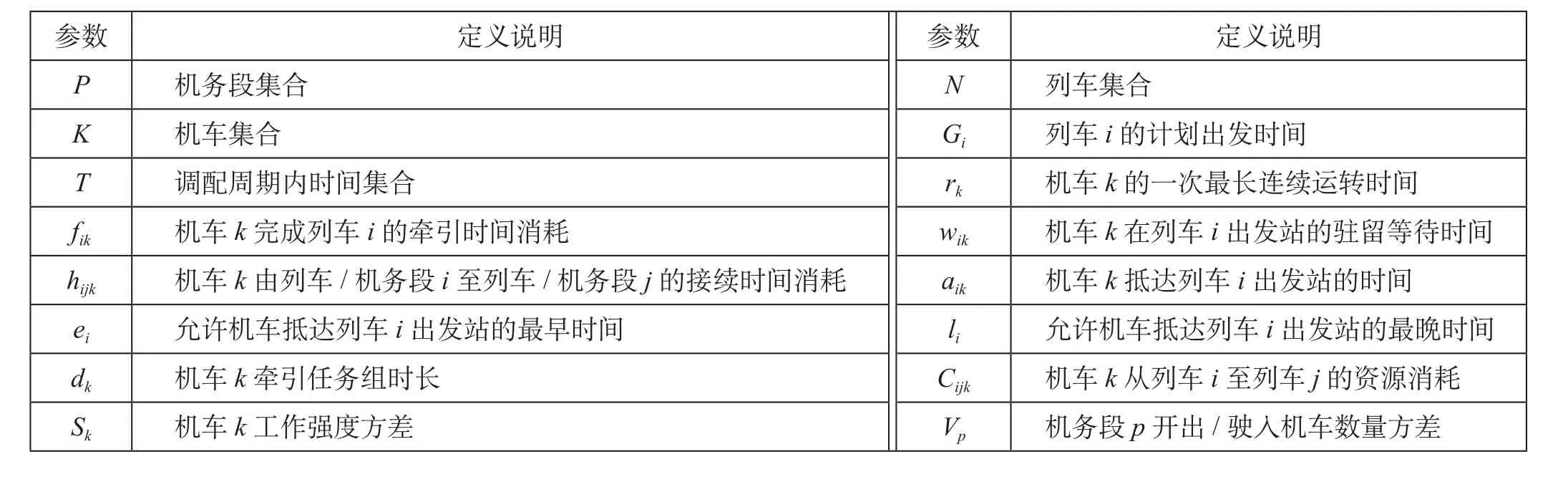
表1 模型涉及的集合和参数Tab.1 Sets and parameters involved in the model

约束 ⑵ 表示机车连续运转的最长时间限制,机车k的运转时间由空驶时间、牵引列车时间和驻留等待时间构成；约束 ⑶ 为机车数量限制；约束⑷—⑼ 表示机车在机务段、牵引任务之间的接续约束：约束 ⑷ 为变量x和变量y的匹配关系；约束⑸ 表示机车满足出入段条件,不要求与其出发机务段相同；约束 ⑹ 和 ⑺ 表示列车与机车的一一对应关系；约束 ⑻ 为机车接续约束,表示机车在牵引完列车i的任务后必须是从i出发；约束 ⑼ 为各个机车交路的“小回路”破坏条件,表示机车k只有从机务段开出后,才能去执行列车的牵引任务；约束 ⑽ 为机车的牵引状态对其能否前往牵引列车的限制；约束 ⑾—⒀ 为时间窗约束：约束 ⑾ 为同一机车牵引的接续列车间的时间匹配约束；约束⑿限制了机车到达牵引列车所在站的时间范围；约束⒀ 为补充条件,规定机务段的到达时间、等待时间和运输任务时间为0。

2.3 求解算法

机车调配问题在本质上是一个混合整数规划问题,一般的数学软件在求解小规模问题时往往能较快找到全局最优解,但规模一旦过大,求解的速度就很难满足需要。此时可以使用启发式算法进行求解,通过设计一种模拟退火算法,可以在较短时间内找到较好的解,下面给出第一阶段(机车不回段的一次连续运转过程)的算法实现步骤。

步骤1：生成初始机车运用方案P0。

步骤2：设置约束条件Const,初始温度T,临界温度e,小循环次数k和降温系数a。

步骤3：开始模拟退火内循环,令I= 0。

步骤4：通过随机条件进行判定,改变机车发出到达的机务段、交换运输任务的牵引机车或合并机车的牵引任务,产生新解P1。

步骤5：若新解P1不满足约束条件Const,则转步骤4。否则令Δ =obj(P1) -obj(P0),若Δ ≤ 0,则令P0=P1；否则生成0到1之间的随机数r=random(0,1),若r＜exp (-Δ /T),令P0=P1。

步骤6：令I=I+ 1,若I＜K,则转到步骤4。

步骤 7 ：令T=αT,若T＜ε,则转到步骤 3。

步骤8：输出第一阶段求解结果P0。

其中,为提高计算效率,初始解的产生方式由下面规则给出。

步骤1：设置剩余列车集N_remain为全部列车任务。

步骤2：令每列列车由距离出发站最近的机务段开出机车进行牵引,对各机车可最早出发时间leavetime进行排序,选择该值最小的一组机车k和列车j,令k前往牵引j；更新N_remain,leavetime。

步骤3：设置机车k可牵引列车集N_left为空,在剩余列车集中寻找满足机车k接续牵引的列车,并加入N_left中。

步骤4：若可牵引列车集N_left为空,则转到步骤7。

步骤5：对机车k到达列车i出发站的时间进行排序,选择该值最小的列车作为机车k的下一牵引列车,更新N_remain,leavetime。

步骤6：若可牵引列车集N_left非空,则返回步骤3。

步骤7：记录列车机车k的牵引列车组,若剩余列车集合N_remain非空,则返回步骤2。

步骤8：输出初始可行解。

第二阶段(牵引任务组的接续过程）同样可以使用这种算法求解,只需将其中的列车改为牵引任务组即可。为了提高问题的求解速度,针对第二阶段本文给出一种启发式规则,实现步骤如下。

步骤1：输入牵引任务组总数N,设置各站整备完成的机车数初始值L均为0。

步骤2：设置选择牵引任务组的初始编号J= 1,设置所需机车总数的初始值n= 0。

步骤3：若牵引任务组J的出发站机车数L(j) ＞ 0,则令最早整备完成的机车执行J,L(j) =L(j) - 1；否则,L(j)开出一台机车执行J,所需机车总数n=n+ 1。

步骤4：若J整备完成,则令J的到达站机车数L(j) =L(j) + 1。

步骤5：令J=J+ 1；若J≤N,则返回步骤3。

步骤6：输出结果。

3 算例研究

通过2个案例对提出的方法进行验证,案例1由随机生成,使用Lingo和启发式算法分别求解,以验证算法的适用性；案例2基于包神铁路的实际运营数据,运用启发式算法求解。所设计的模拟退火算法在MATLAB R2014b平台编程实现,在Intel Core i73.2GHz处理器和16GB主存储器的戴尔NMK500个人电脑上运行。

3.1 模拟案例

某铁路货运区间有7个站,首尾站分别为机务段和折返段所在地,某段铁路各区间走行时间如表2所示。某段时间内开行6列普通列车和1列重载列车,列车运行情况如表3所示。

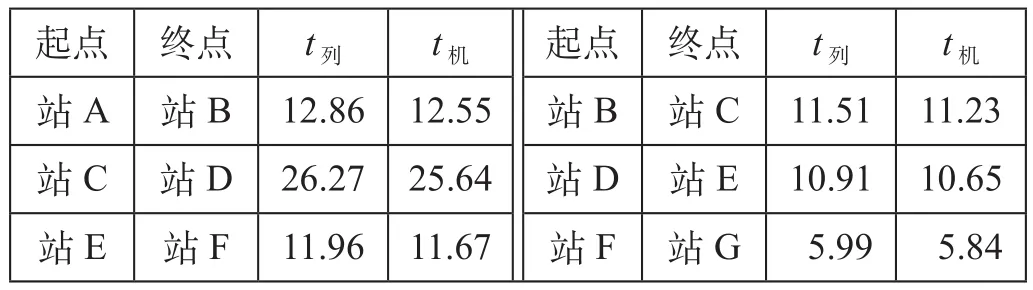
表2 某段铁路各区间走行时间表 minTab.2 Running schedule in each section of a railway

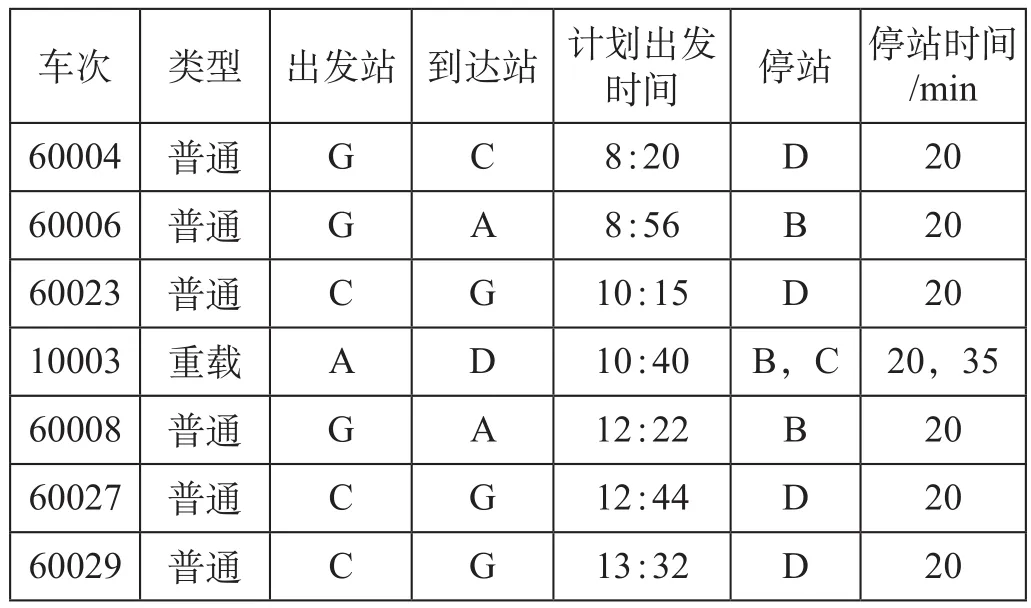
表3 列车运行情况表Tab.3 Train operation table

为简化模型输入,利用“影子”列车来代替重载列车,机车在站整备时长20 min,参数计算表如表4所示。

设置参数(ξ1,ξ2,ξ3) = (1,0,0),分别使用Lingo内置求解器和模拟退火算法求解,模拟退火算法求解机车调配结果方案表如表5所示,算法求解调配结果机车周转图如图5所示。第一阶段解得列车60004和60023组成牵引任务组,列车10003_2和60029组成牵引任务组；第二阶段将列车60008的牵引任务合并到机车k1执行,列车60006和60027的牵引任务合并为机车k2执行。2种方法求解结果比较如表6所示。

以此可看出,启发式算法虽然比Lingo求解结果略差,但运行时间大大缩短,因而所给算法在解决较大规模实际问题时具有可行性。

3.2 包神铁路南线机车调配实例

包神铁路(包头—神木)是国家能源集团煤运通道的重要组成部分,南线为双线铁路,共设置9个车站,包神铁路南线线路如图6所示。该段铁路机车交路较短,导致牵引作业有效时间减小,机车的运用受到影响,调配问题显著。包神铁路南线的机务段位于东胜站,折返段位于乌兰木伦,列车平均速度49.14 km/h,单机走行速度50.35 km/h,该段铁路重载列车都由双机进行牵引。

应用机车调配模型,在考虑资源消耗、强度均衡和工作连续性的情景下进行优化计算。实例选取包神铁路南线2017年7月8日开行的59列重载列车和179列普通列车,包神铁路南线某日列车运行图如图7所示。

表4 参数计算表Tab.4 Parameter calculation table

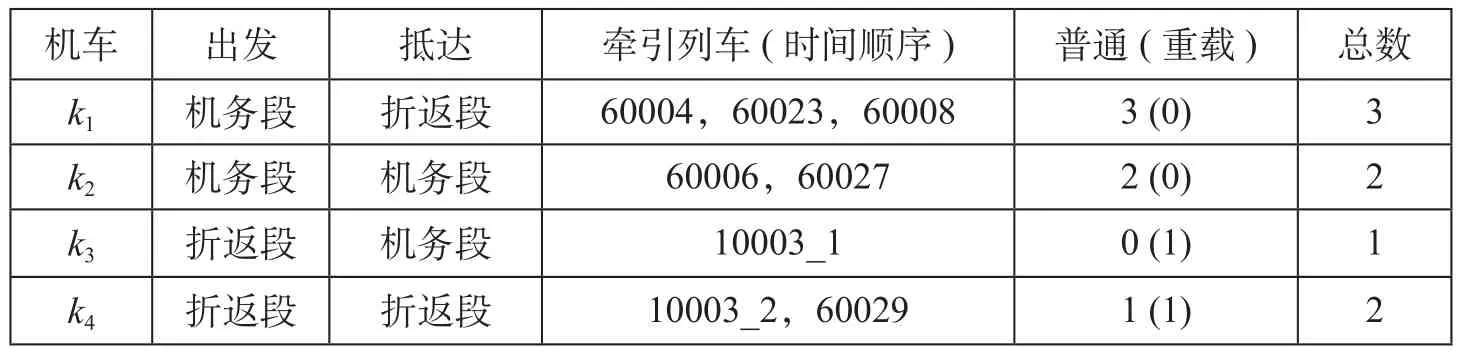
表5 模拟退火算法求解机车调配结果方案表Tab.5 Locomotive assignment plan solving by Simulated Annealing Algorithm

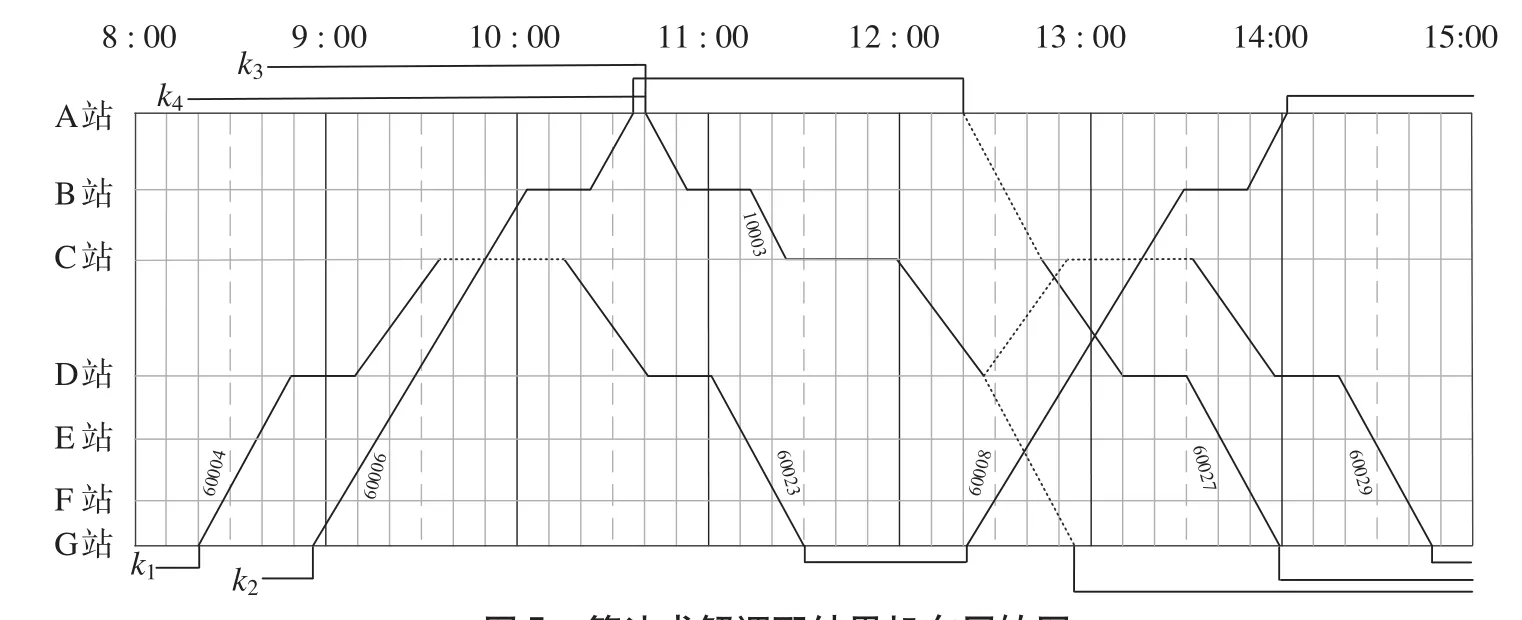
图5 算法求解调配结果机车周转图Fig.5 Locomotive rotation diagram solving by algorithm

表6 求解结果比较Tab.6 Comparison of the results

使用模拟退火算法求解该机车调配问题,不同参数设置下目标函数值如图8所示。

当参数时,目标函数取得最小值4612.65。不同情景下机车调配结果对比如图9所示,只考虑资源消耗优化,参数设置为的机车周转图如图10所示,结果相比于优化前,机车的使用数量大大减少,平均接续时间得到缩短,空驶成本降低。加入机车工作强度均衡和工作接续性2个目标函数,参数设置为,由于机车的工作时间平均化,以及等待成本所占比重降低,使得机车的平均等待时间增长；而为了满足工作连续性而采用的机务段开出/开回机车均衡,使得机车可能由距离列车出发站较远的机务段开出,因而机车平均接续时间略有增长。

图6 包神铁路南线线路图Fig.6 Circuit diagram of Baotou-Shenmu south railway line

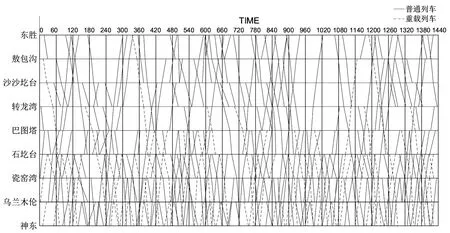
图7 包神铁路南线某日列车运行图Fig.7 Train operation diagram in Baotou-Shenmu south railway line in one day

4 结束语

针对铁路企业开行始发终到站位于中间站列车的机车调配问题,提出了一种两阶段机车调配方法,并对包神铁路南线重载运输通道的机车调配运用进行优化,为铁路机车的灵活调配提供了一种新的思路和途径。由于机车调配在铁路运输组织中并不是一个单独的过程,如果能与机务排班和列车开行方案协同编制,则会使机车的运用效率得到更好地发挥。另外,对于重载列车与普通列车混行的运输组织模式,提出的“影子列车”是一种处理列车输入的方法,虽然能解决该机车调配问题但未能将问题普适化,因而考虑将拖车问题引入并用以解决该类问题是进一步研究的重要方向。

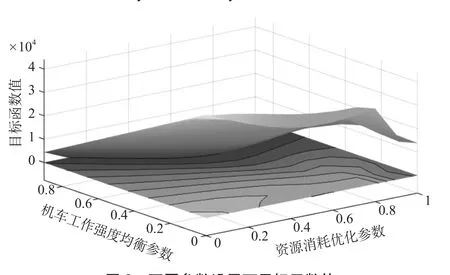
图8 不同参数设置下目标函数值Fig.8 Results under different parameter settings

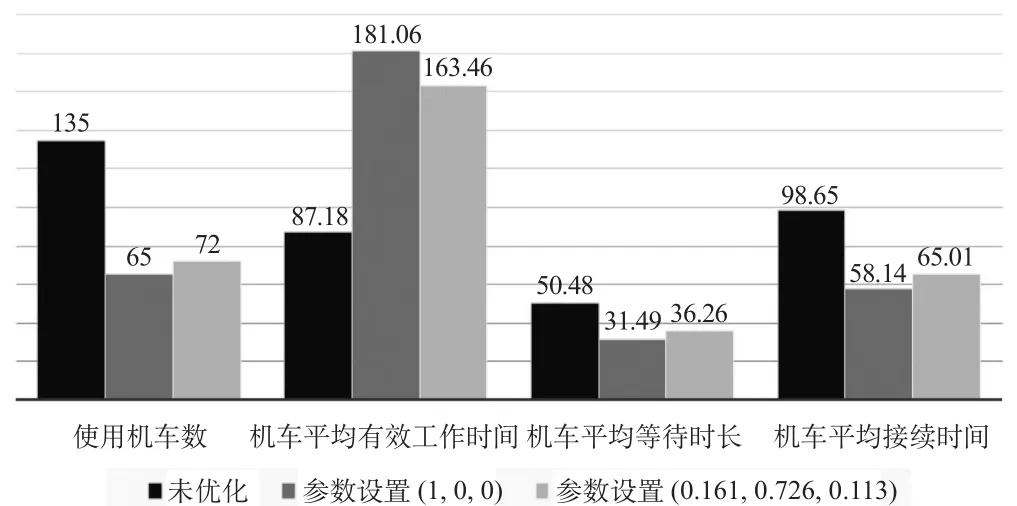
图9 不同情景下机车调配结果对比图Fig.9 Comparison of the locomotive assignment results in various scenarios

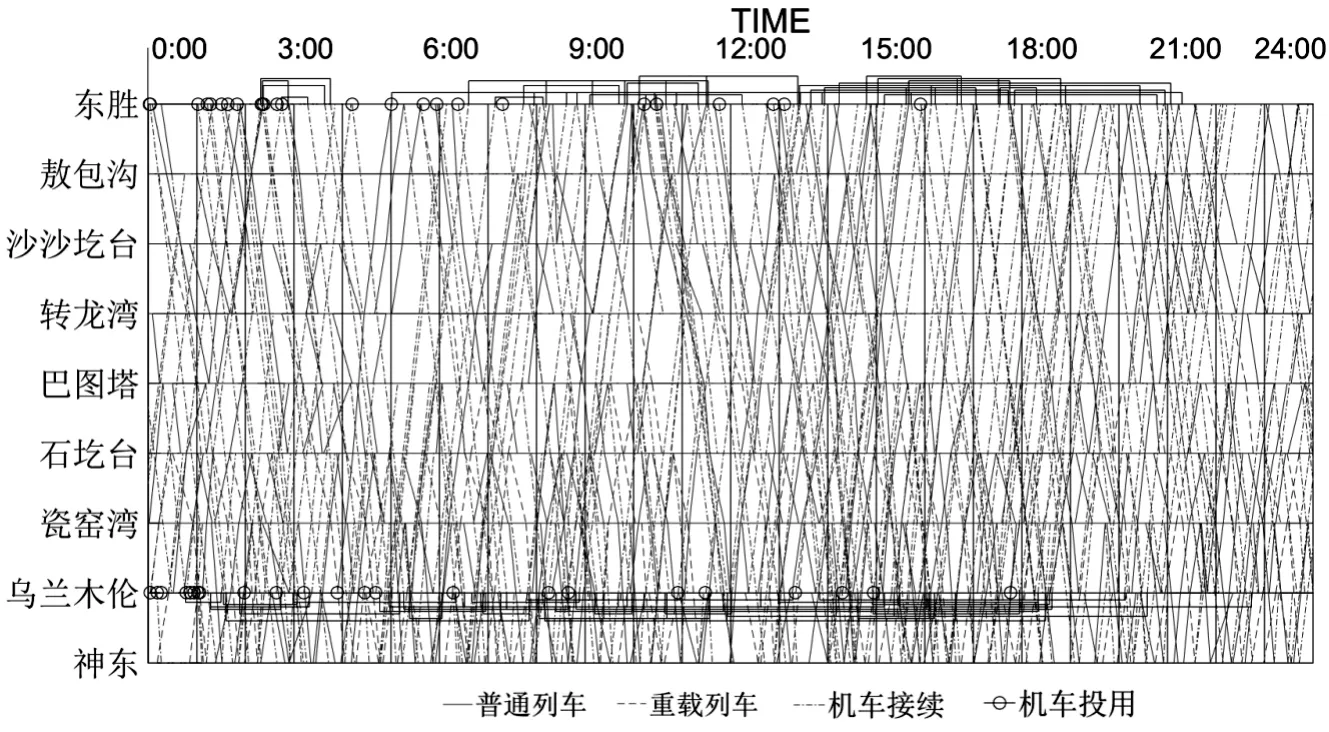
图10 参数设置为(1，0，0)的机车周转图Fig.10 Locomotive turnaround chart when the parameter is set to (1, 0, 0)