函数测试题A 卷

■河南省太康县第一高级中学

一、选择题

1.已知3a=5b=1 5,则a,b不可能满足的关系是( )。

A.a+b＞4

B.a b＞4

C.(a-1)2+(b-1)2＞2

D.a2+b2＜8

2.已知a,b均为正实数,函数y=aex+b的图像过点(0,1),则的最小值为( )。

A.2 B.3 C.4 D.5

3.素数也叫质数,部分素数可写成“2n-1”的形式(n是素数),法国数学家马丁·梅森就是研究素数的数学家中成就很高的一位,因此后人将“2n-1”形式(n是素数)的素数称为梅森素数。已知第2 0个梅森素数为P=24423-1,第1 9个梅森素数为1,则下列各数中与最接近的数为( )。(参考数据:l g2≈0.3)

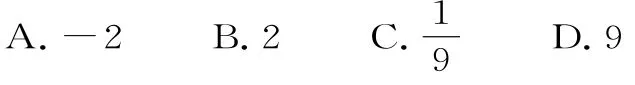
A.2 B.4 C.6 D.8

6.已知函数f(x)=ex+e4-x,则( )。

A.f(x)在(-∞,2)上单调递增,在(2,+∞)上单调递减

B.f(x)在(-∞,2)上单调递减,在(2,+∞)上单调递增

C.函数f(x)的图像不关于直线x=2对称

D.函数f(x)的图像关于点(2,0)对称

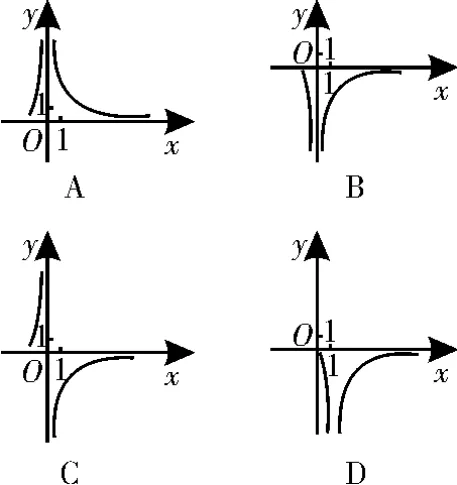
图1

8.函数y=f(x-1)的图像关于点(1,0)对称,当x∈(0,+∞)时,f(x)+x f'(x)＜0成立,若,则a,b,c的大小关系是( )。

9.若函数f(x)=loga(x+1)(a＞1)的图像与函数y=g(x)的图像关于原点对称,且x∈[0,1)时,不等式2f(x)+g(x)≥m2-m恒成立,则实数m的取值范围是( )。

10.已知函数f(x)=l g([x]-x),其中[x]表示不小于x的最小整数,则关于函数f(x)的性质表述正确的是( )。

A.定义域为(-∞,0)∪(0,+∞)

B.在定义域内为增函数

C.周期函数

D.在定义域内为减函数

11.已知幂函数f(x)=(m-1)2·xm2-4m+2在(0,+∞)上单调递增,函数g(x)=2x-t,∀x1∈[1,6)时,总存在x2∈[1,6)使得f(x1)=g(x2),则t的取值范围是( )。

A.∅ B.t≥2 8或t≤1

C.t＞2 8或t＜1 D.1≤t≤2 8

12.已知函数f(x)=函数g(x)=|2f(x)-m|-1,且m∈Z,若函数g(x)存在5个零点,则m的值为( )。

A.5 B.3 C.2 D.1

二、填空题

14.设实数a,b分别满足方程3a2+6a+1=0和b2+6b+3=0,且a·b≠1,则a-3a b-1+b-1的值为

三、解答题

17.化简或求下列各式的值。

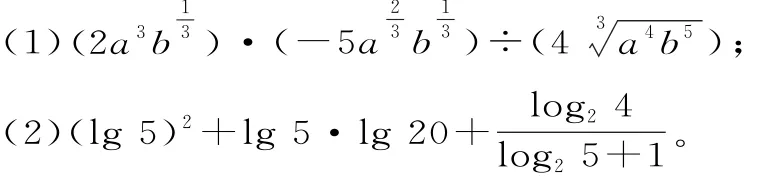
18.已知函数f(x)=ax+b(a＞0,a≠1),其中a,b均为实数。

(1)若函数f(x)的图像经过点A(0,2),B(1,3),求函数的值域;

(2)如果函数f(x)的定义域和值域都是[-1,0],求a+b的值。

19.为了在夏季降温和冬季取暖时减少能源消耗,业主决定对房屋的屋顶和外墙喷涂某种新型隔热材料,该材料有效使用年限为2 0年,每毫米厚的隔热层建造成本为6万元,且每年的能源消耗费用H(万元)与隔热层厚度x(毫米)满足关系(0≤x≤1 0),设f(x)为隔热层建造费用与2 0年的能源消耗费用之和。

(1)请解释H(0)的实际意义,并求f(x)的表达式。

(2)当隔热层喷涂厚度为多少毫米时,业主所付的总费用f(x)最少?若此时与不建隔热层相比较,业主可节省多少钱?

20.幂函数为什么叫“幂函数”呢?幂,本义为方布。三国时的刘徽为《九章算术·方田》作注:“田幂,凡广(即长)从(即宽)相乘谓之乘。”幂字之义由长方形的布引申成长方形的面积;明代徐光启翻译《几何原本》时,自注曰:“自乘之数曰幂”。幂字之义由长方形的面积再引申成相同的数相乘,即xn。

图2

(1)判断函数g(x)=f(1+x)+f(1-x)的奇偶性并求其值域;

(2)若关于x的方程f(x2-t x+8)=2在[1,4]上有解,求实数t的取值范围。

22.已知函数f(x)=(a2-2a-2)logax是对数函数。

(1)若函数g(x)=loga(x+1)+loga(3-x),讨论g(x)的单调性;