基于KPCA和SVM的汽车车身缺陷识别方法

张陈 杨龙兴 刘凯磊 张卫平 施晓芳

摘 要：汽车在长期使用中，车身容易发生疲劳裂纹和腐蚀等缺陷，而车身通常采取多层合金复合材料，因此给检测造成巨大的困难。目前无损检测技术可以有效针对该类型缺陷进行检测和自动分类识别，该技术采用时频域分析手段，实现缺陷的定量检测。在此基础上，进一步提出基于核主成分分析法（KPCA）和支持向量机（SVM）相结合的方法来提高缺陷分类识别准确率。理论分析和实验结果相一致，验证了所采用方法的可行性。

关键词：无损检测;分类识别;时频域分析;定量检测;核主成分分析法;支持向量机

中图分类号：TP216;TG115 文献标识码：A 文章编号：2095-1302（2019）08-00-04

0 引 言

随着汽车使用时间增加，汽车车身结构内部、层状结构第二层之后和紧固件周围会产生裂纹和腐蚀，这些缺陷使得汽车结构遭到严重损坏，造成维护成本逐年上升。及时发现并定量检测缺陷及自动分类识别对于降低汽车维护成本具有非常重要的意义。但是，现有对汽车裂纹、腐蚀缺陷的分类识别方法准确率较低。

传统涡流的激励源[1]采用单一固定频率的正弦波，但是由于涡流趋肤效应作用，对缺陷识别能力有限。脉冲涡流无损检测技术[2-4]采用具有一定占空比方波的激励信号。

针对传统脉冲涡流缺陷分类标准通常只提取缺陷信号的单一特征量，如时间上升点或形状特征量用于缺陷分类识别，或者通过两个特征量组合用于缺陷分类，如峰值和峰值时间，但造成分类识别的准确率依然不高。因此，本文从时、频域中提取用于识别缺陷和裂纹的特征，提出了一种新型的基于核主成分分析法（KPCA）[5-6]和支持向量机（SVM）[7]组合的方法提高缺陷分类识别准确率。

1 脉冲涡流理论分析

脉冲涡流检测是将占空比为一定值的方波信号施加在检测线圈上，该信号会感应出脉冲涡流在被测试件中进行传播。若检测表面上有缺陷存在，会导致检测线圈上的感应电压发生改变。由于脉冲频谱[8]很宽，感应电压信号中包含有缺陷的重要信息，因此特别适合用来检测裂纹和腐蚀缺陷。其脉冲涡流检测机理如图1所示。

为了实现对裂纹和腐蚀的定量检测，脉冲涡流一般提取峰值和过零时间两个特征。检测线圈上的瞬态信号波形如图2所示。

裂纹长度和腐蚀体积的变化会引起峰值变化，裂纹深度会引起过零时间的变化，通过提取峰值和过零时间可实现对汽车车身结构裂纹和腐蚀缺陷的检测。

2 试验装置

脉冲涡流试验装置[9]采用模块化的思想，主要包含4个部分，即方波脉冲信号发生模块、信号调理模块，探头和数据采集模块。其中，探头上的激励脉冲信号由方波脉冲信号发生模块产生，方波信号电压为10 V，频率为100 Hz，占空比为0.5。信号调理模块主要进行检测信号的放大与滤波，是数据采集的一个重要环节。探头由检测线圈和磁传感器组成。其中，检测线圈采用圆柱形，外径为22 mm，内径为

11 mm，高度为5 mm。线圈的线径为0.29 mm，匝数为600，线圈内阻为10 Ω。数据采集模块采用16位、采样频率为100 kHz的PCI9111采集卡。

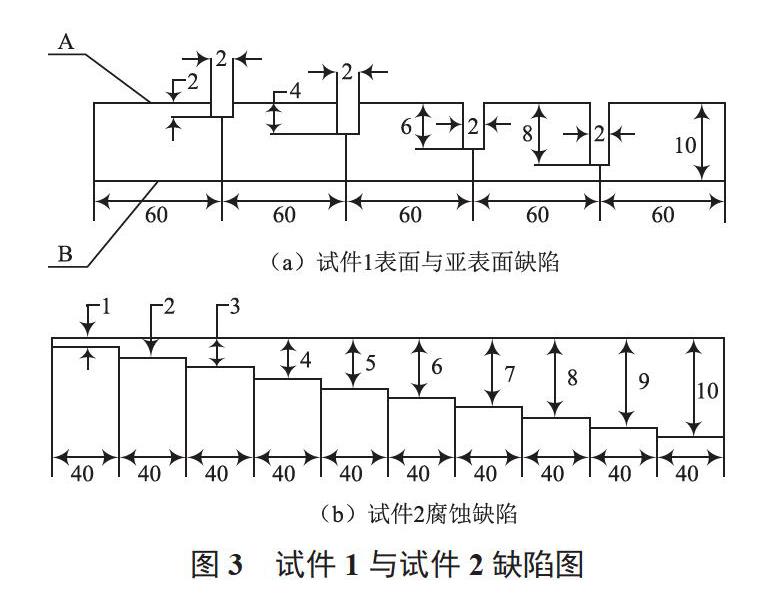
本次试验中，在厚度为10 mm的铝板上加工了不同尺寸的长方体，具体尺寸图见图3。其中，试件1的A面和B面用来模拟汽车车体表面和第二层出现的裂纹缺陷;试件2用来模拟汽车车体结构中出现的腐蚀缺陷。

3 裂纹和腐蚀缺陷检测

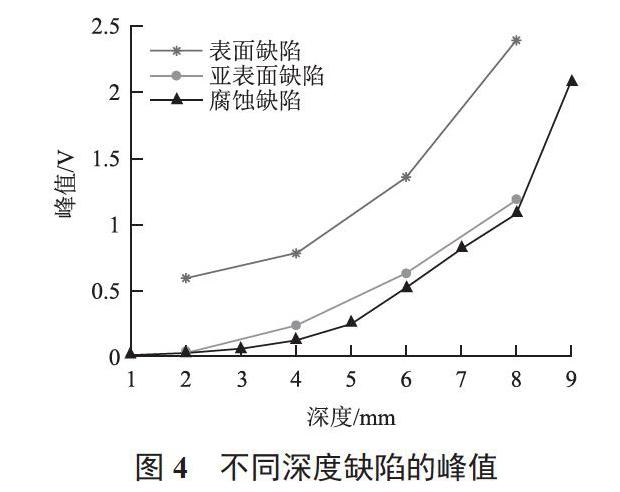
比较表面、亚表面裂纹和腐蚀缺陷，通过提取信号的峰值和峰值时间对其进行深度定量分析，结果见图4和图5。

由图4可以看出，表面、亚表面裂纹和腐蚀缺陷的差分峰值随缺陷深度z近似成正指数函数变化。涡流检测原理公式为

式中：I0表示涡流密度;f表示激励电流频率;σ表示材料电导率;μ表示材料磁导率;z表示缺陷深度。由涡流检测原理公式可以看出，涡流密度I0随缺陷深度z的增加成指数函数下降，说明实验结果与理论一致。

由图5可以看出，表面、亚表面裂纹和腐蚀缺陷的差分峰值时间t与缺陷深度z成线性变化。由于涡流在导体中传播速度为一定值，如果缺陷越深并且顶部离探头越近，就会越早对检测线圈中的涡流产生干扰，导致其峰值时间越短。

通过提取脉冲涡流差分信号的频谱的基频分量，对铝合金试件（a）的表面缺陷与亚表面缺陷以及铝合金试件（b）腐蚀缺陷进行分析，如图6所示。

由图6可以看出，表面、亚表面裂纹和腐蚀缺陷的基频分量频谱幅值随缺陷深度的增加而增大，变化趋势近似成指数型，其增长特性和峰值与缺陷深度变化关系一致;而且在相同深度时，腐蚀缺陷的基频幅值相比亚表面缺陷更大。和峰值、峰值时间与缺陷深度关系比较，基频幅值明显更容易受缺陷深度的影响。因为宽脉冲的能量正好集中于低频分量处，缺陷的基频幅值对腐蚀缺陷和亚表面缺陷检测识别更

有效。

4 自动分类识别

4.1 核主成分分析法

为了更好地处理非线性数据，核主成分分析法通过引入一个非线性映射函数Φ，将原空间中的数据映射到高维空间;然后在高维空间中使用PCA方法提取主成分[10]，在保持原数据信息量的基础上达到降维的目的。具体步骤描述如下：

（1）先獲取数据集，然后对数据集进行无量纲化处理，从而可以得到输入样本X=[x1，x2，…，xl]。

（2）计算l×l维核矩阵K=（kij）l×l，但要提前选取适当的核函数，本试验选取的是高斯径向核函数，如下：

（3）计算在高维空间中对映射的非线性数据进行中心化后的核矩阵。

（4）求解核矩阵的特征值λ1，λ2，…，λl。

（5）求解核矩阵特征向量v1，v2，…，vl。

（6）将λ1，λ2，…，λl按从大到小排列，使特征向量与其一一对应，然后单位化特征向量。

（7）计算特征值的累积贡献率Q。通常取累积贡献率达85%～95%的特征值λ1，λ2，…，λm所对应的第1个、

第2个、…、第m（m≤p）个主成分。

本试验将裂纹和腐蚀缺陷检测信号中提取的多个特征量作为KPCA的训练数据，然后按照KPCA具体步骤进行处理。结果见图7，可以看出KPCA能有效识别出上述三种缺陷。

4.2 支持向量机原理

支持向量机是由Vapnik等首先发现并提出的，它是建立在统计学习理论的VC维理论和结构风险最小原理基础上来完成的。其基本原理是（以二维数据为例，如图8所示）：在图中实心圆和空心圆代表两类样本，分类超平面是H，支持向量是直线穿过的点，其离H超平面最近。H1与H2是经过两类支持向量的平面，并与超平面H平行，它们到H超平面的距离是分类间隔。假设训练样本集合为（xi，yi），其中，i=1，2，…，n;x为输入量;x∈Rd;i为样本数;y∈

（-1，1）。在输入空间维数为D时线性判别函数的一般形式为g（x）=w·x+b，所以分类面方程为：

在实际应用中，先对分类超平面H进行归一化处理，再建立SVM的数学模型，使两类样本满足|g（x）|≥1的条件。这样分类间隔就等于2/||w||，使||w||2最小。支持向量到最优分类超平面H的距离为1/|w|，其求解可以看作一个二次优化问题：

对于样本数据线性不可分时，Vapnik等在优化问题上加一个ξ1≥0的松驰项来构造最优分类超平面，将条件放宽为：

式中C称为惩罚算子，控制对错分样本的惩罚程度。显然，当划分错误时，ξi>0。因此，在求分类平面的同时，希望Σξi越小越好。

通过非线性变换φ（x）将输入空间变换为高维特征空间。φ（x）通过给定恰当的核函数来实现，则：

利用K（xi，xj）代替线性可分情况下的最优分类平面的点积（xi·xj），就是把原有的特征变换到一个新的特征空间，则目标优化函数可表示为：

求解后，得到最优分类判别函数：

式中：K（xi，x）为核函数;sgn（·）为符号函数;l为训练样本的数目。

目前常用核函数主要有：线性核函数，K（x， y）=x·y;多项式核函數，;高斯径向核函数，;多层感知器核函数，。

文献[11]指出，核函数及其参数的选择会直接影响支持向量机识别的正确率。但是每个核函数都各有优缺点，因此在使用时仅仅使用一个核函数往往不能使支持向量机识别的正确率达到最高，而混合核函数能够拥有其组成中的普通核函数的优点。文献[11]还得出多项式核函数外推能力较好，并且外推能力随着阶数的降低而增强;高斯径向核函数较多项式核函数具有较好的学习能力，并且学习能力会随着参数σ的减小而增强，但外推能力较差。本文选用的混合核函

数为：

K（x，y）=ρ1K多项式+ρ2K高斯径向                     （11）

式中，ρ1和ρ2为两个单一核函数在混合核函数中的比重。

本文借助文献[12]提出的平衡约束规划（MPEC）模型优化选取参数的方法，解决了核参数及权函数的选取问题，选择ρ1=0.9，ρ2=0.1，d=2，σ=0.7。最终选择的混合核函数为：

（12）

经过前面提取的时域特征值可以看出，表面缺陷可以100%分离出来，但亚表面和腐蚀缺陷还存在许多交涉部分。接下来针对亚表面和腐蚀两种缺陷在核主成分分析法提取脉冲涡流信号特征基础上进行支持向量机处理，结果见图9。可以看出图中黑色圈的地方很少，分类识别的正确率明显提高。

对试件1和试件2再进行重复性试验，测试结果见表1。

分析表1可以发现，采用核主成分分析法（KPCA）+支持向量机（SVM）相结合的方法进行试验，分类识别准确率得到明显提高。

5 结 语

本文针对传统脉冲涡流分类识别方法准确率较低的问题，提出一种新型的基于核主成分分析法（KPCA）和支持向量机（SVM）的方法，并采用平衡约束规划（MPEC）模型优化选取参数的方法，确定了支持向量机采用混合核函数中的参数，来提高缺陷分类识别的准确率。理论分析和实验结果一致，验证了所提方法的可行性。

注：本文通讯作者为杨龙兴。

参 考 文 献

[1] YANG B F，LI X C. Pulsed remote eddy current field array technique for nondestructive inspection of ferromagnetic tube [J]. Nondestructive testing & evaluation，2010，25（1）：3-12.

[2] SMITH R A，HUGO G R. Transient eddy current NDE for ageing aircraft-capabilities and limitations [J]. Insight：non-destructive testing and condition monitoring，2001，43（1）：14-25.

[3] MOULDER J C，BIEBER J A，WARD W W，et al. Scanned pulsed eddy current instrument for nondestructive inspection of aging aircraft [J]. Proceedings of the SPIE，1996，2945：2-13.

[4] LI S，HUANG S L，ZHAO W. Development of differential probes in pulsed eddy current testing for noise suppression [J]. Sensors & actuators a physical，2007，135（2）：675-679.

[5]孙韶媛，李琳娜，赵海涛.采用KPCA和BP神经网络的单目车载红外图像深度估计[J].红外与激光工程，2013，42（9）：2348-2352.

[6] LU J W，PLATANIOTIS K N，VENETSANOPOULOS A N. Face recognition using kernel direct discriminant analysis algorithms [J]. IEEE transactions on neural networks，2003，14（1）：117-126.

[7] VAPNIK V N. The nature of statistical learning theory [M]. Berlin：Springer，1995.

[8]张玉华，孙慧贤，罗飞路.层叠导体脉冲涡流检测中探頭瞬态响应的快速计算[J].中国电机工程学报，2009，29（36）：129-134.

[9]南玉龙，杨龙兴，阚仁峰，等.基于KPCA的脉冲涡流缺陷分类识别技术的研究[J].物联网技术，2017，7（2）：66-69.

[10] 贺光琳.电涡流检测系统开发及缺陷反演算法研究[D].杭州：浙江大学，2008.

[11] SMITS G F，JORDAAN E M. Improved SVM regression using mixtures of kernels [C]// International Joint Conference on Neural Networks. Honolulu：IEEE，2002：2785-2790.

[12] DONG Y L，XIA Z Q，WANG M Z. An MPEC model for selecting optimal parameter in support vector machines [C]// The First International Symposium on Optimization and Systems Biology. Beijing：The First International Symposium on Optimization and Systems Biology，2007：351-357.