水下流场模拟可视化渲染绘制方法研究

包雪怡

摘要：在3D水下场景渲染中融入流场的模拟可视化是增强现实领域近年来研究工作的重点之一。水下流场模拟可视化框架，包括流场模拟和可视化渲染绘制两部分。流场模拟基于N-S方程，温度为唯一的输入参数。为了更准确描述水体温差、密度不均匀导致的对流现象，浮力作为流上下浮动的外力项;同时，通过波浪扰动项描述流和水面波动的一致性。可视化渲染绘制部分，采用基于纹理的直接体渲染（Direct Volume Rendering， DVR）和一维的转移函数（transfer-function）描述流场特征，展现时变流场数据（温度，速度，压强等）。框架通过GPU引擎对上述算法进行加速，结合上帝之光实时模拟可视化时变流场的扰动效果，满足场景实时交互可视化渲染绘制需求。

关键词：水下场景;流场模拟;体渲染;可视化;增强现实

中图分类号：TP319.41        文献标识码：A

文章编号：1009-3044（2019）19-0223-03

穿过水面的光线会与水中粒子发生碰撞形成上帝之光和焦散等奇妙的光学现象。同时温度、密度和压强等的变化会引起水体内对流和扩散等现象。隐藏在这些现象下的本质就是流体动力学。流模拟需要昂贵的计算开销，而且渲染绘制流体不能依赖传统的基于光栅化渲染平台实现，因此实时流动态模拟可视化渲染绘制仍然是一个具有挑战性的课题。

本文构建水下流场模拟可视化框架，实现水下场景中流扰动过程的模拟和可视化渲染绘制。模拟阳光穿透水面和水流发生相互作用时产生的复杂的光学现象，结合体渲染和后处理体积光生成算法增强流特征。

文章从下面几部分介绍相关工作：流场模拟可视化框架，包括流场模拟N-S方程求解、基于纹理的直接体渲染，实验结果分析、未来的改进方向等。

1 研究背景

流场模拟技术可归纳为两个范畴：基于粒子的拉格朗日方法和基于网格的欧拉方法。本文流场模拟采用基于网格的欧拉方法。

Stam [1]是第一位采用网格欧拉方法模拟流现象的研究者。欧拉流场模拟方法遵循克林形式（Chorin-style），采用操作符分割方法和对流-投影方法来对流施加不可压缩的条件限制。传统的对流-投影框架采用半拉格朗日对流方法，该方法可提供无条件的稳定性。近十年来许多基于该框架的方法被提出用以处理不同的流场模拟问题。Kang et al. [2] 引进了一个GFM（GhostFluidMethod）方法模拟多种状态的不可压缩流体，该方法被Hong and Kim[3]采用对流体的表面变化进行追踪，采用半拉格朗日对流和粒子集（PLS）扩展了该方法。Kang et al.[4]扩展了GFM，模拟可融合和不可融合的流之间的相互作用。基于网格的流场模拟方法也被用来模拟高粘度的流现象。Carlson et al.[5]在MAC（Mark And Cell）框架上采用一个隐式的粘度方程来模拟高粘度的流和融化效果。Goktekin et al[6]采用黏性和塑性系数模拟粘弹性的流现象。最近，Larionov et al[7]在一个压力-粘度求解器中采用基于网格的离散化方法来模拟高粘度的牛顿流体。

为兼顾性能和渲染质量，本文采用基于屏空间的体渲染方法来渲染时变3D流体数据。

2 流场模拟可视化框架

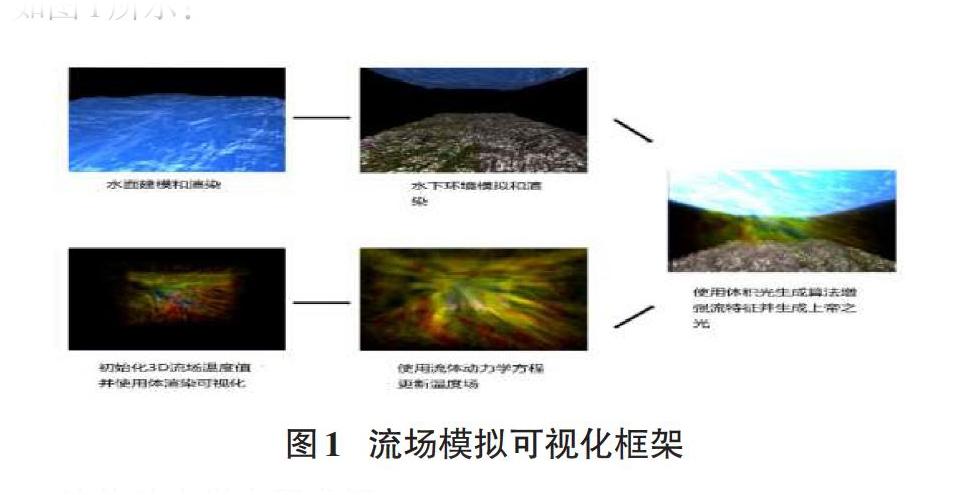
本文框架包含大量的纹理渲染技术，由可编程着色器实现，N-S方程求解的流体动力学运算采用CUDA加速。为渲染一个真实的水下场景以增强流体渲染的视觉冲击力，框架还包括水面的建模和渲染、水下焦散和上帝之光的模拟。框架结构如图1所示：

2.1流体动力学方程求解

本文采用基于网格的流场模拟方法对N-S方程进行求解。为了展现水下流和水面一致的波动，在N-S方程中加入波浪扰动和浮力两个外力项。波浪扰动项描述风对水体的推动而形成的加速度，浮力项模拟水体中温差引起的对流现象。框架实现的流场模拟被限制在一个3D的立方体区域内。假设流的体积在水中的特定深度保持不变，水中流的运动可以由不可压缩流体的N-S方程来描述：

2.2直接体渲染

流体数据集（速度和温度）存储在3D数组中，数据集的每一帧采用公式（1）得到的速度场进行更新，采用DVR技术可视化渲染时变流体数据。公式（14）计算沿视线方向累积光强和模糊度，其中[Ci]是样本点颜色，[Aj]是模糊度，用来模拟光线到达样本点j的衰减状况：

3 结论

水下流场模拟可视化框架采用OpenGL和GLSL实现。框架对渲染海面和水下光照采用的法线贴图方式实现参数化控制。计算量最大的部分是流体动力学方程的求解。其中FFT法线贴图的计算在Cuda上进行。在一张64╳64的2D网格上生成FFT波浪，在一张64╳64╳[64]的网格上模拟流和采用DVR可视化流特征。为了兼顾效果和性能，在低分辨率的网格上生成波浪高度场，采用高分辨率的法线贴图渲染水面。当法线贴图的分辨率增加后，海面会呈现更多高频的波浪，水下也可以看到更多波动的细腻光束，如图8所示。为了求解流体动力学方程，本文采用30次雅各比迭代来求解扩散项，采用50次迭代进行投影操作。根据实验结果，在计算扩散项时，采用20次以上的迭代可以得到比较小的误差。在本文的模拟中，[?x]=[?y=?z]=1/64=0.0156，dt = 0.1，粘度系数[γ]=0.001。

参考文献：

[1] Stam J. Stable Fluids[C].Siggraph，1999，99：121-128.

[2] Kang M， Fedkiw R P， Liu X D. A boundary condition capturing method for multiphase incompressible flow[J]. Journal of Scientific Computing，2000，15（3）：323-360.

[3] Hong J M， Kim C H. Discontinuous fluids[C].ACM Transactions on Graphics （TOG）.ACM，2005，24（3）：915-920.

[4] Kang N， Park J， Noh J， et al. A hybrid approach to multiple fluid simulation using volume fractions[C].Computer Graphics Forum.Wiley/Blackwell（10.1111），2010，29（2）：685-694.

[5] Carlson M， Mucha P J， Van Horn III R B， et al. Melting and flowing[C].Proceedings of the 2002 ACM SIGGRAPH/Eurographics symposium on Computer animation.ACM，2002：167-174.

[6] Goktekin T G， Bargteil A W， O'Brien J F. A method for animating viscoelastic fluids[C].ACM Transactions on Graphics （TOG）.ACM，2004，23（3）：463-468.

[7] Larionov E， Batty C， Bridson R. Variational stokes： a unified pressure-viscosity solver for accurate viscous liquids[J].ACM Transactions on Graphics （TOG），2017，36（4）：101.

[8] Mitchell J. Light shafts： Rendering shadows in participating media[C].Game Developers Conference，2004.

【通聯编辑：朱宝贵】