基于局部差分隐私的表情包收集机制

陈航 张帅奇 曾庆馗

摘要：数据分析公司通过收集用户的信息来了解某一群体的统计数据，例如通过收集用户聊天时发送的最频繁的表情包来获取人群的情感分析。然而这一过程中却可能存在着隐私泄露的问题，针对这一特殊情景，本文基于局部差分隐私算法，将其应用在表情包频数收集的环境当中，通过模拟数据的多轮测试和实验，得到了该算法的可用性分析，实验结果表明本文所采用的方法可以很好地解决表情包收集的隐私保护问题。

关键词：局部差分隐私;表情包收集;隐私保护

中图分类号：TP311      文献标识码：A

文章编号：1009-3044（2019）19-0208-03

1介绍

伴随网络技术的不断发展，互联网企业数量暴增，互联网企业需要对获得用户的统计信息以更好地提供服务。通常这些公司会将数据送往第三方数据分析公司进行数据分析，然而在收集用户信息以改善用户体验的过程中也产生了隐私泄漏的问题。包括在数据的本地存储，数据的传输和数据的云端存储各个环节中都有类似的安全事件不断爆出。例如华住酒店的大量酒店数据泄露并在暗网上销售[1]， Facebook泄露用户隐私并进行违法滥用[2]。

面对隐私保护日益严峻的形势，如何保障用户的隐私并解决隐私泄露问题已成为当下热门的讨论话题。k-anonymity[3]、l-diversity[4]、t-closeness[5]等方法相继被提出用于隐私数据的保护，这些方法提供了一些隐私保护思路，但是这类隐私保护方法会通过不同的攻击方法而泄露敏感信息例如链接攻击[6]。差分隐私[7]作为目前最为流行的隐私保护方法，解决了以上方法存在的问题并定义了隐私保护程度。

传统的差分隐私模型以中心为基础，用户收据收集到服务商进行聚合，对数据库进行添加噪声从而发布带有噪声的中间件以提供查询服务。然而，这个过程中存在不可信服務商的问题，第三方服务者存在将隐私泄露的风险，例如内部员工泄露和遭受恶意攻击。局部差分隐私[8]针对不可信第三方服务者，提出了更加合理的隐私保护方法，通过对用户端发送的数据进行扰动，在服务器端聚合扰动数据的方式来提供差分隐私保障。

在不可信第三方数据分析平台分析数据时，存在的隐私泄露风险可以通过局部差分隐私模型消除。本文以不可信第三方数据收集者收集用户表情包为例，实现基于局部差分隐私的表情包收集机制，在提供隐私保障的同时保持较高的数据可用性，通过实际环境部署进行试验测试。

2 基本概念

定义 局部差分隐私：给定n条用户的隐私记录，对于数据集中的任意两条记录d和d′，若算法A作用于两条记录的结果是相同的，且都为[d*]，即满足如下的关系式，则称A算法满足[?]-局部差分隐私，其中e称为隐私保护预算，其值越大，数据可用性越高，越小，对用户隐私保护的效果越好。

即攻击者凭借已有的背景知识，即使知道了算法A的输出也不能轻易推断出输入到底是对应哪一条记录，提供了不可确定性。

其中本文应用的HCMS（Hadamard Count Mean Sketch）[9]算法引入的随机噪音，在原始的输入上添加噪音，是满足差分隐私定义的，首先客户端算法是A，对于两个数据条目d和d′，得到相同的输出[d*]的概率是相近的。

3 算法

假设一个用户a给用户b发送了一个表情emo1，客户端算法首先根据哈希函数的范围初始化一个独热向量v，然后在k个哈希函数中随机选取一个哈希函数hj，然后通过选取的哈希函数hj将表情emo1编码成一个索引，然后把v的第hj（emo1）位比特置为1，然后对向量v进行Hadamard基变换得到向量w，然后随机选取向量w中的某一位以概率（ee+1）-1进行随机翻转，最后向服务器端发送噪声报告s。

算法1：HCMS（Hadamard Count Mean Sketch）客户端算法

输入：用户的某个属性值d∈D，隐私预算[?]，哈希散列函数列表

输出：扰动位w，哈希函数索引j，扰动位索引

1） 首先从k个哈希函数中随机选取一个，记下其索引j

2） 初始化一个m位的向量v，初始值为0

3） 把v的第[hj（d）]位设为1

4） 构建一个大小为m的阿达马矩阵Hm，使w=Hmv

5） 在v中随机抽取一个位，记下其索引l

6） 按概率（ee+1）-1随机翻转[wl]比特位，翻转后的向量记为[w]

7） 返回报告s{[w]，索引j和索引l）

算法2：HCMS（Hadamard Count Mean Sketch）服务端算法

输入：n条用户记录{（[w（1），j（1），l（1）]），…， （[w（n），j（n），l（n）]）}，隐私预算[?]，哈希函数个数k和向量长度m

1） 使[c?=e?+1e?-1]

2） 初始化长度为n的x二维数组

3） 对于每一个i∈[n]，使[x（i）=k·c?·w（i）]

4） 初始化一个{0}k*m维度的Mh矩阵

5） 通过Mh=MhHmT将矩阵的行转换回来

6） 计算属性值d的频数[f（d）=（mm-1）（1kl=1kMl，hl（d）-nm）]

7） 返回每个属性值的频数f（d）

为了进一步的解释此算法，假设用户访问网络域名www.example.com。客户端算法从一组候选散列函数{h1，h2，h3，...，hk}中选择一个随机哈希函数，并使用选择的哈希函数h1将web域编码到一个小空间中，我们令h1（www.example.com）=33。这个编码被写成一个独热向量v=（0， 0， ...， 0， 1， 0， ...， 0， 0），其中，第33位置的值为1。想要传输一个比特，一个简单的方法就是从向量v中采样并发送一个随机坐标，然而，这会显著增加结果直方图中的误差（方差）。为了减少方差，在v中使用Hadamard基变换矩阵H，以获得V′=Hv=（+1，?1，…，+1）。例如，有一个从V′中采样获得的随机坐标，相应的比特以概率（ee+1）-1进行翻转，从而确保满足e-差分隐私。发送到服务器的报告s包括所选的哈希函数的索引、采样的坐标索引和隐私化比特。

服务器端算法使用的是数据结构Sketch矩阵M，将从客户端那里收集到的隐私向量进行聚合。M矩阵的行向量为哈希函数的索引，列向量是由样本的随机坐标的索引。矩阵的第（j， l）元素聚合了设备所提交的隐私化向量，即从向量中选择第j个哈希函数hj，并采样第l个坐标。继而进一步对私有化向量进行适当的扩展，使用可逆Hadamard矩阵将M转换回原来的基底中。在这个阶段，矩阵的每一行都有助于为元素的频率提供一个无偏差估计量。要计算一个web域www.example.com的频率，这个算法首先通过读取j行的M[j，hj （www.example.com）]以獲得M中每一行的无偏差估计，最后计算出这些k估计的平均值以减少方差。

4 实验

实验环境设置，CPU：i7-7700hq，内存：16G，实验所用数据聚为模拟数据集使用均匀分布和拉帕拉斯分布随机生成的数据集。使用MAPE（平均绝对值百分比误差）作为实验衡量标准，为减小分布偶然性波动对实验的准确率影响，每个实验运行10次，以验证概算的可靠性。

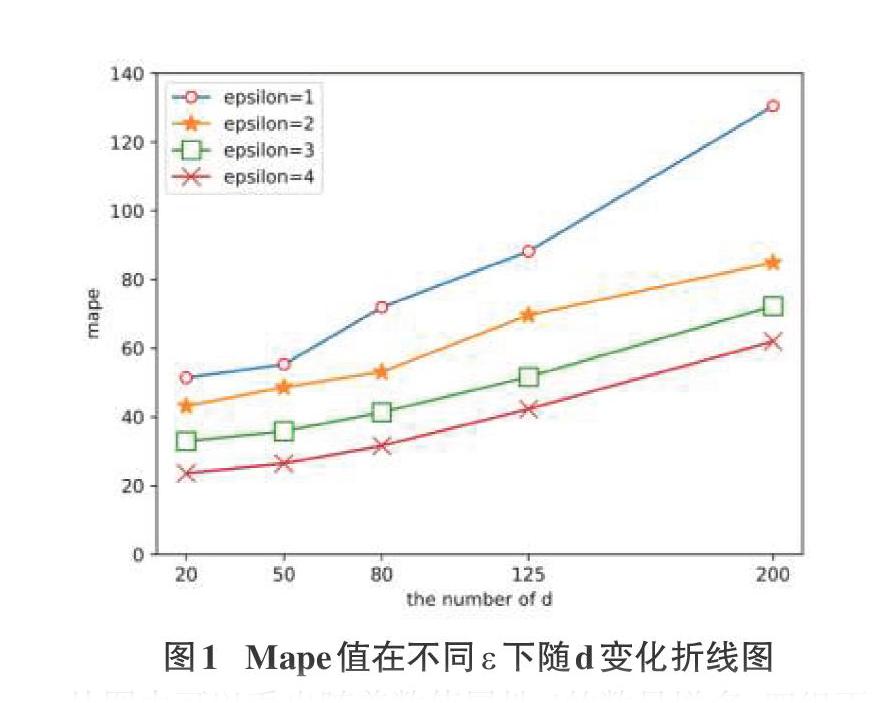
在实验设置中分别控制m和k不变，以验证e和d的改变对实验造成的影响，在选定k=8192， m=256， n=100000的条件下生成十组满足均匀分布的模拟数据，通过服务器端算法进行聚合获得每个属性的估计值，如图1所示。

5 结论

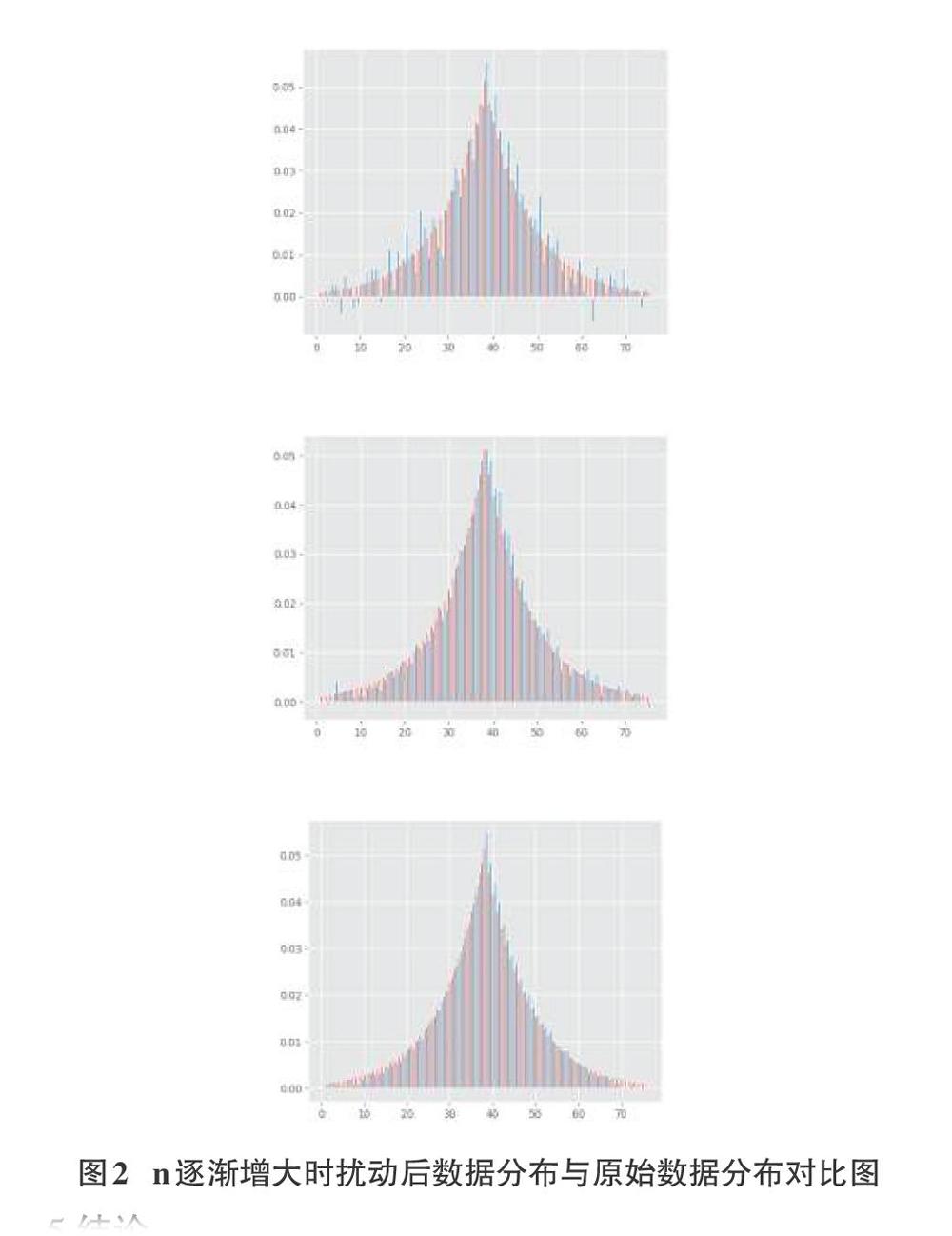
针对收集表情包频数这一具体问题，提出了如何保护用户隐私的同时高效的收集数据，采用了局部差分隐私机制作为收集方法，通过实际浏览器插件模拟真实收集场景，并部署服务器端算法以收集数据。最后通过仿真实验对算法机制进行讨论，该机制可以很好地保持原始数据分布的特征，在数据效用和隐私保障方面有很好的效果。然而还存在一些不足的地方，当数据量较小时，数据可用性较差，以及参数的最优化选取等问题。之后将对这机制进行改进研究，更高效的收集数据信息同时保护用户的隐私。

参考文献：

[1] https：//www.sohu.com/a/250601044_100216761

[2] https：//www.sohu.com/a/226062595_460436

[3] L. Sweeney. k-anonymity： A model for protecting privacy. International Journal of Uncertainty[J]. Fuzziness and Knowledge-Based Systems，2002，10（5）： 557～570.

[4] A. Machanavajjhala， D. Kifer， J. Gehrke and et al..l-diversity： Privacy beyond k-anonymity[C]. ACM Transactions on Knowledge Discovery from Data （TKDD） 1， no. 1 （2007）： 3

[5] Li， Ninghui， Tiancheng Li， and Suresh Venkatasubramanian. t-closeness： Privacy beyond k-anonymity and l-diversity[C].2007 IEEE 23rd International Conference on Data Engineering. IEEE， 2007.

[6] 杨高明，方贤进，肖亚飞.局部差分隐私约束的链接攻击保护[J].计算机科学与探索，2019， 13（02）：251-262.

[7] Dwork， Cynthia. Differential privacy[J]. Encyclopedia of Cryptography and Security ，2011： 338-340.

[8] Duchi， John C.， Michael I. Jordan， and Martin J. Wainwright. Local privacy and statistical minimax rates[C].2013 IEEE 54th Annual Symposium on Foundations of Computer Science. IEEE， 2013.

[9] Differential Privacy Team Apple. Learning with privacy at scale. Technical report， Apple， 2017

【通联编辑：梁书】