Canopy和K-means聚类算法在公交IC卡数据分析中的应用研究

杨健兵

摘   要：通过收集南通市市区公交线路名称和站点名称，在不依赖GPS定位数据的基础上，采用Canopy和K-means聚类算法分析乘客上车时间序列，从而建立乘客上车站点的理论模型，并在Hadoop平台上用MapReduce框架實现算法的并行化。最后，以南通公交IC刷卡记录为例，用Canopy算法和K-means算法对IC卡刷卡记录进行分析。实验表明，在Hadoop平台，用Canopy和K-means算法分析公交IC卡数据运行稳定、可靠，具有很好的聚类效果。

关键词：IC卡;Canopy;K-means;聚类

1    国内外关于公交IC卡的研究

传统的公交客流调查大多数通过问卷调查获得，这种调查方法相对原始、落后，耗费大量的人力、物理和财力，并且最终获得的数据也不精确，往往为最终决策带来一定误差。伴随着智能公共交通系统的发展和普及，公交IC卡收费系统、全球定位系统（Global Positioning System，GPS）监控系统、车辆监控系统中积累了大量原始的公交数据，特别是公交IC卡收费系统，里面保存每位乘客的上车刷卡信息，这些海量的刷卡信息内部蕴含着真实、全面的公交客流信息[1-2]，如何利用数据挖掘技术从这些海量的公交IC卡数据中快速获取真实、全面的公交客流信息，是研究的热点问题。

最近几年，国内外学者在公交IC卡数据分析中做了大量的研究工作。在国外，Jinhua结合城市轨道交通自动售检票系统（Automatic Fare Collection System，AFC）及应用可视性与控制（Application Visibility and Control，AVC）数据获取上车站点，然而国外的城市公交系统与国内的相差很大。在国内，戴宵等[3]提出了对公交卡乘客的刷卡时间进行聚类分析判断乘客上车站点的方法，于勇等[4]结合公交运营调度时刻表所提供的车辆及其发车信息，推算各车次到达各站点的时间，提高了上车站点推算精度。周锐[5]提出了基于IC卡数据的公交站点客流推算方法。赵鹏[6]基于成都公交IC卡数据的乘客上下车站点推算方法研究。徐文远等[7]基于公交IC卡数据的公交客流统计方法。以上的研究存在数据不完整、准确率偏低等问题，研究的正确性很难得到保证。

本文针对公交IC卡中海量的刷卡数据，利用Canopy和K-means聚类算法，在底层分布式文件系统（Hadoop Distributed File System，HDFS）支持下利用MapReduce框架，先用Canopy聚类算法对公交IC卡数据进行预处理，根据得到的类别数再用K-mean算法对公交IC卡刷卡数据进行分析。

2    数据预处理

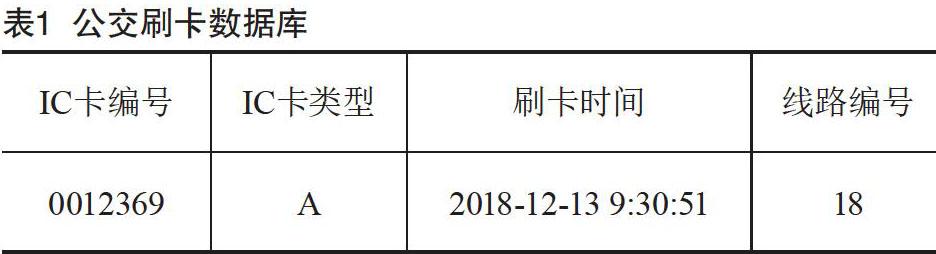
本文需要处理的数据来源于于南通公交IC刷卡记录，IC卡刷卡数据如表1所示。

公交在行驶的过程中停靠站点具有单一性，即从起点站依次经过各个站点最终达到终点站。同时，乘客的刷卡记录具有次序性，即上车站点前的刷卡时间早于上车站点后的刷卡时间。如果乘客乘车站点相同，该站点乘客间刷卡时间相差不大，如果乘客乘车站点不同，则乘客刷卡时间相差很多。

所以可以得出结论：如果乘车站点相同，则乘客刷卡时间相差间隔不大;如果乘车站点不同，则刷卡时间间隔很多。这样可以把刷卡间隔差距不大的进行聚类，使得相同乘车站点的刷卡记录聚为一类，不同乘车站点的刷卡记录为不同类。

3    聚类算法

3.1  K-means算法

K-means算法把对象组织成多个互斥的组或簇，采用距离作为相似性的评价指标。假设数据集D包含n个欧式空间中的对象，聚类的目的是把D的对象分配到k个簇C1，…，Ck中，使得对于1≤i，j≤k，Ci∈D且Ci∩Cj=￠。聚类的划分的目的使得簇内高相似性和簇间低相似性为目标。

设数据集集合D={x1，x2，…，xn}，xi={xi1，xi2，…，xir}，xj={xj1，xj2，…，xjr}，则样本xi和xj之间的欧式距离为： d（xi，xj）=（1）

误差函数平方和如下：

Jc=（2）

其中，k为聚类数目，ri是第i类样本的个数，ni是i类样本的平均值。

K-mean均值的算法复杂度为O（nkt），其中，n是对象总数，k是用户指定的簇数，t为迭代次数。通常情况下k<

K-means算法的优点是算法简单，易于实现，而且收敛速度快，计算工作很快就能完成。但是K-means算法也存在着一些缺点，在聚类之前K-means算法需要提前制定k的值，在k值没有确定的情况下，K-means算法无法运行。

3.2  Canopy算法

与传统的聚类算法（K-means）不同，Canopy聚类最大的特点是不需要事先指定k值（即clustering的个数），因此，具有很大的实际应用价值。与其他聚类算法相比，Canopy聚类算法虽然精度较低，但在速度上有很大优势，因此，可以使用Canopy聚类先对数据进行“粗”聚类，得到k值，以及大致的k个中心点，再使用K-means进行进一步“细”聚类。Canopy算法的具体步骤如下。

（1）原始数据集合list按照一定的规则进行排序（该规则是任意的，一旦确定就不再更改），初始距离阈值为T1和T2，且T1>T2（T1，T2的设置可以根据用户的需要或者使用交叉验证获得）。

（2）在list中随机挑选一个数据向量A，使用一个粗糙距离dist计算方式计算A与list中其他样本数据向量之间的距离d。

（3）根据（2）中的距离d，把d小于T1的样本数据向量划分到一个Canopy中，同时，把d小于T2的样本数据向量从候选中心向量名单（这里理解为list）中移除。

（4）重复步骤（2）和（3），直到候选中心名单为空，即list空，算法结束。

算法原理比较简单，就是对数据进行不断遍历，T2

3.3  K-means和Canopy算法在Hadoop平臺下的实现过程

在Hadoop平台中K-means算法和Canopy算法可以用MapReduce程序来实现。首先，用Canopy程序开发实现k类簇，这个k个类簇可以作为K-means算法初始化条件，最终使用K-means聚类实现最终的结果。Mapreduce的程序设计与实现如图1所示。

3.4  乘客上车站点判断

由于我国绝大多数城市公交乘车采用上车刷卡的形式，并且刷卡记录只是记录上车时刻，并无上车站点信息，所以通过Canopy算法和K-means聚类算法对刷卡时间序列进行聚类分析后，可以得出这些刷卡记录被分为k种不同的类簇，在同一类簇中，上车站点相同，不同的类簇上车地点不同。因此，下一阶段要完成类和公交站点的匹配。在公交行驶过程中，有时候所有站点都有人刷卡上车，有时候有些站点没有人刷卡上车，所以要实现类簇和站点匹配需要分两种情况进行讨论。

设站点总数为S，站点从始发站到终点站的序列依次为s={1，2，3，……，S}，第i个站点和第i+1个站点的长度记为d（i，i+1）。该线路的总长可以通过累加相邻两个站点的距离所得：D=

（1）第一种情况，所得聚类数=公交站点总数-1，即k=S-1。此情况表明每个站点都有人进行刷卡，所以可以根据刷卡时间的先后次序，将类簇中的刷卡时间与各个站点依次进行匹配即可。

（2）第二种情况，通过Canopy算法得到的聚类数数量小于公交站点总数-1，即k

由于公交车在行驶启动时由驾驶员刷卡，所以聚类后第一类刷卡记录所对应的站点是公交线路的第一个站点，所以可以从第二类开始进行估计。

当估计第二类的上车站点时，设可以匹配的站点序号为{2，3，4，…，S-1}，其中，没有乘客上车的站点有S-1-k个，记为Δs1，即Δs1=S-1-k，因此，第二类的上车站点要从候选站点序列（2，2+1，2+2，……，2+Δs1）站点中选择一个。

设公交车全程行驶距离是D，根据驾驶员两次刷卡记录（即始发站刷卡和终点站刷卡）可以计算出公交车全程运行时间T，这样公交车平均速度V=D/T。

在估计第二类的上车站点时，设第一类与第二类之间的行驶距离Δd （l，2），Δd （l，2）=V×（Tk1-Tk2）， Tk1和Tk2为第一类和第二类刷卡时间的平均值。

以第一类上车站点与每一个候选站点间的固定距离d（k1，k1+i），再依次计算公交车行驶距离Δd（l，2）与每一个固定距离d（k1，k1+i）之间差的绝对值，绝对值最小的即为第二类的上车站点。

完成第二类上车站点的估计后，用同样的方法来估计第三类的上车站点，以此类推，当无刷卡记录站点减少为零时，表明剩余的待匹配站点都有乘客上车，则可以实现剩余站点刷卡记录与余下公交站点一一匹配。

4    实验结果

4.1  实验环境

在本实验中，使用2台服务器搭建Hadoop平台，每台服务器采用intel至强处理器，内存大小为128 G，使用Centos7作为网络操作系统，搭建ambari大数据管理平台，包括一个master节点和一个slaver节点，来运行K-means和改进的K-means算法。

4.2  实验结果

实验数据选取南通18路公交2018年7月18日一次行驶过程的刷卡记录，数据记录共81条，通过匹配南通18路公交22个站点，经过分析后得出每个站点刷卡人数如表2所示。

5    结语

本文针对南通公交缺乏GPS调度数据的情况下，利用公交IC卡刷卡记录，通过聚类算法来对刷卡记录进行聚类，根据聚类的结果来推算出每个站点刷卡人数，实验表明，该算法可靠有效，可以精确地匹配到每个站点上车人数。通过对数据的研究，可以合理地安排公交调度，极大地提高公交的运行效率。

[参考文献]

[1]孙慈嘉，李嘉伟，凌兴宏.基于云计算的公交OD矩阵构建方法[J].江苏大学学报（自然科学版），2016（4）：456-461.

[2]陈锋，刘剑锋.基于IC卡数据的公交客流特征分析—以北京市为例[J].城市交通，2016（1）：51-58，64.

[3]戴霄，陈学武，李文勇.公交IC卡信息处理的数据挖掘技术研究[J].交通与计算机，2006（24）：40-42.

[4]于勇，邓天民，肖裕民.一种新的公交乘客上车站点确定方法[J].重庆交通大学学报，2009（1）：121-125.

[5]周锐.基于IC卡数据的公交站点客流推算方法[D].北京：北京交通大学，2012.

[6]赵鹏.基于成都公交IC卡数据的乘客上下车站点推算方法研究[D].成都：西南交通大学，2012.

[7]徐文远，邓春瑶，刘宝义.基于公交IC卡数据的公交客流统计方法[J].中国公路学报，2013（5）：158-163.

Research of canopy and K-means clustering algorithm in data analysis of the bus IC card

Yang Jianbing

（Nantong College of Science and Technology， Nantong 226007， China）

Abstract：By collecting the names of bus routes and stations in Nantong city， this paper uses canopy and K-means clustering algorithm to analyze passenger boarding time series， and then establishes the theoretical model of passenger boarding point on the basis of not relying on GPS positioning data. Then the parallel algorithm is implemented in the framework of MapReduce on Hadoop platform. Finally， taking the IC card record of Nantong bus as an example， the paper uses canopy algorithm and K-means algorithm to analyze the IC card record. Experiments show that using canopy and K-means algorithm to analyze bus IC card data on Hadoop platform runs steadily and reliably， and has good clustering effect.

Key words：IC card; Canopy; K-means; clustering