高温服装热度分布的研究

何笑笑 刘可盈 王吉桓 王蒙蒙 赵阳君

摘   要：在高溫环境下，为避免灼伤，穿专用服装对人身安全至关重要。首先，文章利用Matlab绘制出温度变化图，获得其变化规律;其次，根据密度等专用服装材料的参数值，建立傅里叶热传导方程模型;再次，利用抛物型方程的差分解法以及对温度分布条件进行离散化，求出方程优化结果;最后，得到I～IV层温度分布的离散化函数，并得出结论：颜色区域越深，表示温度越高。以此帮助更好地设计高温专用服装。

关键词：Matlab;傅里叶热传导方程模型;偏微分方程

1    问题提出和分析

1.1  问题提出

为了设计高温专用服装，将体内温度为37 ?C的假人放置在实验室的高温环境中，测量假人皮肤外侧的温度。为了降低研发成本、缩短研发周期，本研究利用数学模型来确定假人皮肤外侧的温度变化情况[1]。

1.2  问题分析

考虑到工作者在不同温度的环境以及穿着不同材料的服装，人体温度和部位的皮肤温度不同，首先，本研究基于温度和时间的变化规律，绘制出温度变化图;其次，利用拟合得到温度与时间的关系函数;最后，根据每个织物材料层都有热传导率ki（i=1，2，3，4）、密度等参数值，建立傅里叶热传导方程模型。但鉴于稳态之前有一个过程，故利用抛物型方程的差分解法以及对温度分布条件进行离散化，求出方程优化结果。

2    模型建立和求解

2.1  模型建立

首先，根据热量守恒定律，计算单位时间内从单位体积内放出的热量Q，则从t1到t2这段时间内热源所提供的热量为：

（1）

其中，F（x，y，d，t）表示热源强度，Q表示热源提供的热量。

又由于各织物材料层是均匀的，但厚度不一样，因此，各织物材料层则转化为三维热传导方程为：

（2）

其中，u=u（t，x，y，d）表示温度，它是时间变数i与空间变数（x，y，d）的函数;ki为此材料层的热传导率，ci为比热ρi（i=1，2，3，4）为密度，都是已知的常数，且，。

其次，通过对数据拟合得到假人皮肤外侧的测量温度关于时间的函数关系式，建立抛物型方程，利用差分的方法求出其近似的数值解[2]。

在网格内点（k，j）处，一维热传导方程可分别表示为：

基于以上模型分析，用x，y，d表示I，II，III织物层，根据如下的计算方法得出：

故将原问题转化为：

2.2  模型求解

首先，能够明确知道的是，环境温度即为第I层左侧开始传导的温度，第IV层右侧即为假人皮肤的温度，对90 min实验数据进行观察，可知初始时刻人体温度为37 ℃，时间在1 745 s人体温度变为48.08 ℃，并在此以后保持不变。我们对0 s和1 745 s这个过程的数据利用Matlab软件进行九阶拟合，皮肤温度与时间拟合关系如图1所示。

由图1可知，粗线为原始数据曲线，细线为拟合的九阶曲线图，可以看到拟合曲线很好地进行了拟合，得出假人皮肤外侧的测量温度随时间的变化函数为：

（8）

最后，综合考虑以上建立的模型和数据拟合方程，对温度分布条件进行离散化，求出方程优化结果：

（9）

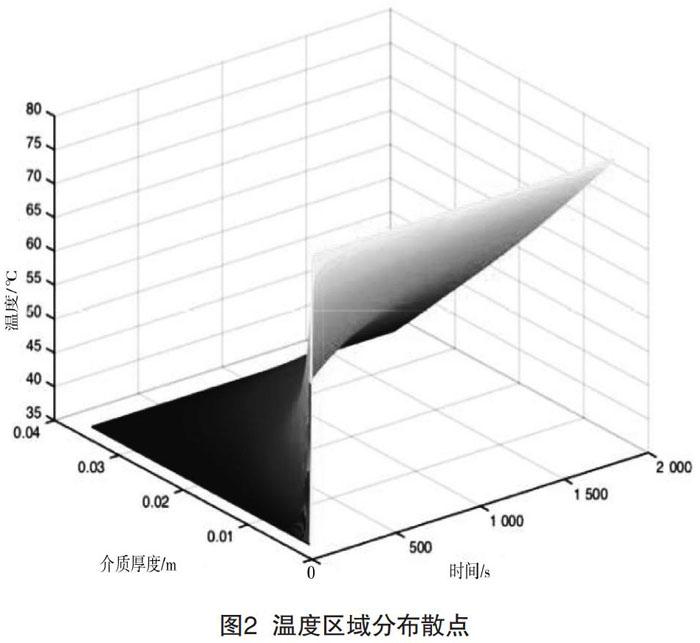
将优化结果代入上述的优化函数中，得到I层到IV层离散化温度区域分布散点图[3]，如图2所示。

根据图3可以得到I层到IV层温度区域的三维分布散点图，对应不同的时间和材料距离，对应的温度也不同，其中，温度由浅绿到深蓝，颜色越深，温度越高。

2.3  结果分析

通过对时间与温度的数据进行拟合，得到温度与时间的关系函数，建立傅里叶热传导方程模型，利用抛物型方程的差分解法以及对温度分布条件进行离散化，求出方程优化结果，并代入优化函数中，最后得到I层到IV层温度分布的离散化图像，得出不同的时间和材料距离，就会产生不同的温度，并且颜色越深，温度越高。

[参考文献]

[1]runok工作室.2018年全国大学生数学建模竞赛A题[EB/OL].（2018-09-14）[2019-06-10].https：//blog.csdn.net/sdwujk160507140150/article/details/82707400.

[2]姜启源，谢金星，叶俊.数学模型[M].3版.北京：高等教育出版社，2003.

[3]吴建国.数学建模案例精编[M].北京：中国水利水电出版社，2005.

Research on heat distribution of high temperature garment

He Xiaoxiao， Liu Keying， Wang Jihuan， Wang Mengmeng， Zhao Yangjun

（School of Computer and Information Engineering， Henan Normal University， Xinxiang 453000， China）

Abstract：In high temperature environment， in order to avoid burns， wearing special clothing is important to personal safety. First of all， the paper uses Matlab to draw the temperature change chart and get its change rule. Secondly， the Fourier heat conduction equation model is established according to the parameter values of special clothing materials such as density. Secondly， using the differential solution of parabolic equation and discretization of temperature distribution conditions， the optimization results of equations are obtained. Finally， the discretization function of the temperature distribution of I～IV layer is obtained， and it is concluded that the deeper the color area is， the higher the temperature is. This helps to better design special high-temperature clothing.

Key words：Matlab; Fourier heat transfer equation model; partial differential equation