深厚覆盖层中局部强透水层对渗流的影响研究

王正成， 毛海涛,2， 申纪伟， 黄海均

(1.重庆三峡学院 土木工程学院， 重庆 404100； 2.武汉大学 水利水电学院， 湖北 武汉 430072)

1 研究背景

深厚覆盖层地基广泛分布于我国西南、西北地区[1]，随着水利水电工程的迅速发展，基岩出露或薄覆盖层的地基越来越少，受到地基的约束，越来越多的水利工程不得不建立在深厚覆盖层地基上[2]。研究表明，深厚覆盖层地基中往往存在局部强透水层，强透水层具有孔隙大、透水性强等特性，其特性决定了强透水层是渗流的优先和集中通道，是控渗工程的薄弱环节[3]。因此，为了保证工程的安全稳定，制定合理可靠的渗控方案，局部强透水层对大坝渗流的影响规律亟待探明。

大量学者以局部强透水层为研究对象，开展了研究。谢辉[4]借助Seep3D针对底部为强透水的特殊基坑工程进行了三维非稳定渗流模拟，结果表明防排结合的方式能有效控制基坑内的降水。常明云等[5]提出针对砂卵石地层复杂强透水地层进行处理时，应针对强透水通道进行回填充填灌浆堵漏处理。崔永高[6]研究表明含有强透水层的超大面积基坑在降水时存在着较强的群井效应。刘晓庆等[7]针对强透水地基上土石坝进行非饱渗流数值模拟，得出辐射井和集水廊道联合作用能有效收集水库渗水。李桂荣等[8]针对郑州引黄灌溉调蓄池的强透水层进行研究，提出了“塑性混凝土+水平壤土铺盖”联合控渗方案。叶青[9]研究表明采用止水帷幕针对强透水基坑进行控渗处理时，随着帷幕深度增大，控渗效果越佳。李来祥等[10]提出采用高喷帷幕截渗方案对高瞳泵站的强透水地基进行控渗处理，效果显著。曹洪等[11]以双层强透水层堤基为研究对象，研究表明强透水层间的垂向渗流作用较弱，强透水层层内流动及越流补给作用显著。综上所述，已有研究成果主要集中在强透水基坑及地基存在的弊端及处理方式，或优化渗流计算模型。但针对深厚覆盖层中局部强透水层深度、厚度及连续性等特性对渗流场的影响尚缺乏系统的研究，需深入探讨。

2 非饱和土体渗流理论

土-水特征曲线(SWCC)用于描述饱和-非饱和土中土体体积含水率与基质吸力间的函数关系，本文采用Van Genuchten提出的数学模型[12]：

(1)

式中：Vws为标准化体积含水量；a为进气压力值的倒数；um为基质吸力；n为与土体孔径分布相关的参数；m为SWCC曲线的整体对称性参数。

孔隙水在表面张力作用下，在水、气截面产生弯液面，水和气承受的压力存在差异，该差异值称为基质吸力，此力是非饱和土的一个重要指标，通过Laplace公式可求解得出[13]:

(2)

式中：ua为孔隙气压力，Pa；uw为孔隙水压力，Pa；Ts为表面张力，N；r1和r2为弯液面短轴和长轴半径，m。

非饱和渗透特征曲线可采用Gardner[14]提出的非饱和渗透系数与基质吸力关系式:

(3)

式中：k为表征土体的非饱和渗透系数；ks为饱和渗透系数；γw为水的容重，kg/m3。

土体孔隙率、饱和渗透系数和初始饱和渗透系数间的关系为：

(4)

式中：ks0为初始饱和渗透系数；n为孔隙率；n0为初始孔隙率。

非饱和土渗流控制微分方程[15]为:

(5)

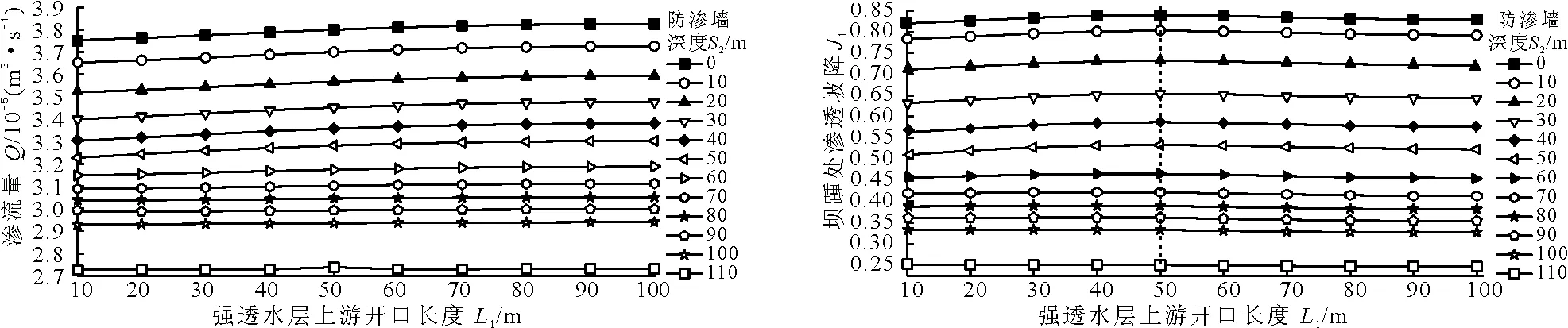
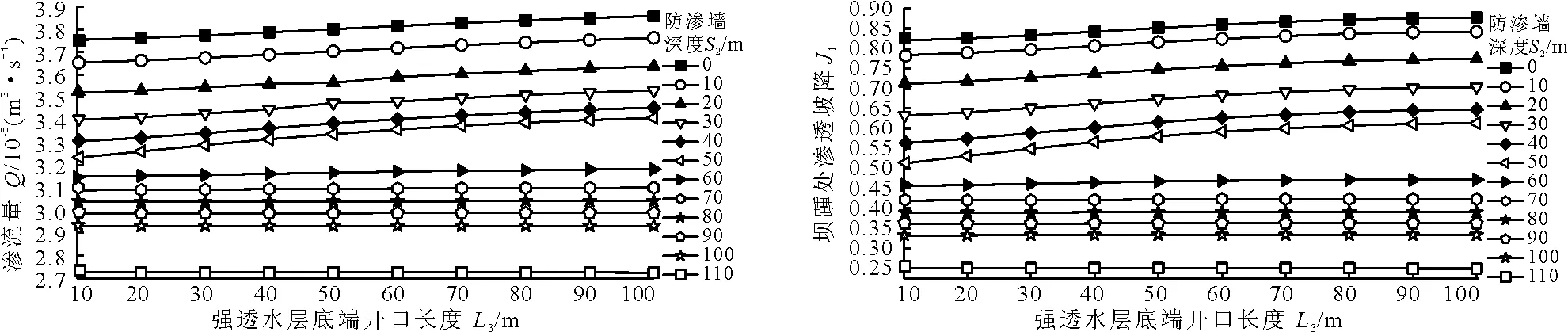
式中：kr(hc)为相对透水率，非饱和区0

3 模型建立

3.1 模型概况

坝体为黏土均质土坝，坝高20 m，坝顶宽5 m，坝前和坝后水头为16和0 m；上下游坝坡均为1∶2。深厚覆盖层地基厚度为110 m，为典型的强弱互层地基，由砂土(强透水层)和黏土(弱透水层)构成，坝体和坝基中的黏土为同一种材料；坝基的控渗方案为混凝土防渗墙，防渗墙嵌入坝体内2 m，墙体厚1 m，深度S2为0～110 m(图1)。

3.2 计算工况

经调查研究表明，由于受到地质成岩作用、地质构造运动等因素的影响，深厚覆盖层坝基中局部强透水层的埋深(深度)、厚度、连续性存在较大差异，且局部强透水层往往是渗流的集中通道，是控渗工程的重点处理对象，决定整个控渗工程的成败的关键因素。

基于强透水层特性(深度、厚度和连续性)的差异，建立数值模型：(1)厚度：强透水层厚度d=1 m，深度S1=10～100 m，如图1(a)所示；(2)深度：强透水层深度S1=55 m，厚度d=1～10 m，如图1(b)所示；(3)连续性：强透水层深度S1和厚度d分别为55和1 m，其上游、下游和底端开口长度分别用L1、L2和L3表征，在10～100 m间取值，如图1(c)～1(e)所示。

3.3 计算参数

将黏土、强透水层和防渗墙的基本物理参数列入表1。

表1 数值模型土体的基本物理指标

非饱和砂土和黏土在渗流作用下，流体和固体发生耦合作用，体积含水率Vws和渗透系数k随基质吸力变化，变化曲线如图2所示。

图1 5种工况模型横断面图

图2 体积含水率和渗透系数随基质吸力的变化曲线

4 模拟结果与分析

基于上述数值模型，分别计算出各工况下渗流量Q、坝踵处渗透坡降J1、出逸坡降J2，旨在分析强透水层深度S1、厚度d和连续性对大坝渗流的影响。

4.1 强透水层深度分析

作渗流量Q随强透水层深度S1的变化曲线，如图3所示。

由图3可得，(1)曲线1～2变化规律类似，渗流量Q随强透水层深度S1的增大而减小；当S1由10 m增大至100 m时，曲线1、2对应的渗流量Q分别降低20.06%、21.36%，且初始降低速度较快。(2)曲线3～11变化规律类似，存在明显的分界线，当S1≤S2时(分界线以下区域)，渗流量随S1增加而增大，增幅为8.61%～18.26%；当S1≥S2时(分界线以上区域)，渗流量随S1的增大而降低，降幅为1.04%～14%。(3)当S2=110 m时，为全封闭式防渗墙，曲线近似水平；当S1由10 m增加至100 m时，渗流量仅增大1.6%。

进一步分析坝踵处渗透坡降J1的变化规律，其变化曲线如图4所示。

对比图3与4可得，渗流量和坝踵处渗透坡降的变化规律类似，皆存在明显的分界线，但也存在些许差异。(1)当S1≥S2时(分界线以上区域)，坝踵处渗透坡降J1随S1的增大而降低，降幅为7.92%～33.49%；(2)当S1≤S2时(分界线以下区域)，坝踵处渗透坡降J1先降低，随后近似趋于稳定，最后再增大；以曲线5(S2=40 m)为例进行阐述说明，当S1由10增大至20 m时，坝踵处渗透坡降J1降低15.67%；S1由20增大至30 m时，J1仅增大1.38%；S1由30增大至40 m时，J1增大40.74%。

进一步分析出逸坡降J2随强透水层深度S1的变化规律，其变化曲线如图5所示。

由图5可得，各曲线的变化特征存在共性，总体呈下降趋势，且初始下降速度较快，随后逐渐趋于稳定；当S1由10 m增加至100 m时，出逸坡降J2降低6.17%～6.81%。但对比各曲线也存在一定差异：(1)当防渗墙深度S2≤20 m和S2=110 m时，出逸坡降呈下降趋势；(2)当30≤S2≤100 m时，出逸坡降J2曲线存在明显的分界线，J2先降低后增大，随后再降低，最后趋于稳定；(3)当S1=S2时，出逸坡降J2增大，增幅为0.05%～0.48%。

基于各渗流参数随强透水层深度S1的变化特性，进一步分析渗流参数随强透水层厚度d的变化规律。

4.2 强透水层厚度分析

当强透水层深度S1=55 m时，作渗流量Q随强透水层厚度d的变化曲线如图6所示。

图3渗流量随强透水层深度的变化曲线 图4坝踵处渗透坡降随强透水层深度的变化曲线

图5出逸坡降随强透水层深度的变化曲线 图6渗流量随强透水层厚度的变化曲线

由图6可得：(1)当防渗墙深度S2=0～50 mS1=55 m时(曲线8～11)，防渗墙穿过强透水层，渗流量曲线变化平缓，当d由1 m增大至10 m时，渗流量Q仅增大0.38%～2.39%。(4)当S2=110 m时(曲线12)，为全封闭式防渗墙，曲线近似水平，当d由1 m增大至10 m时，渗流量Q仅减小0.07%。

进一步分析坝踵处渗透坡降J1的变化特征，其变化曲线如图7所示。

对比图6与7可得，渗流量和坝踵处渗透坡降曲线的变化规律类似，当防渗墙深度S2=0～50、70～100 m时，强透水层厚度由1 m增加至10 m时，坝踵处渗透坡降J1增大0.31%～11.67%；当防渗墙深度S2=60 m时，d由1 m增加至10 m时，J1增大46.8%；当防渗墙深度S2=110 m时，d由1 m增加至10 m时，J1降低0.82%。当d由5 m增大至6 m时，曲线7对应的渗流量增大26.11%。

作出逸坡降J2的变化曲线如图8所示。

对比图6～8不难得出，3个渗流参数的变化规律类似，出逸坡降J2的特性参照J1和Q的变化规律，不再赘述。但出逸坡降明显大于坝踵处渗透坡降，J1=0.243～0.908，J2=20.837～21.521。

基于上述规律，进一步分析强透水层的连续性对渗流场的影响，设定3种工况：强透水层上游开口、下游开口、底端开口。

4.3 强透水层连续性分析

4.3.1 强透水层开口在防渗墙上游 作渗流量Q随强透水层上游开口长度L1(下文简称“上游开口长度”)的变化曲线如图9所示。

由图9可得，各曲线变化规律类似，曲线平缓。当S1=0～100 m，Q随上游开口长度L1的增加而增大，增幅为0.31%～2.36%。当防渗墙深度S1=110 m时，为全封闭式防渗墙，Q随着L1的增大上下波动，但总体呈增大趋势，增幅为0.15%。

作坝踵出渗透坡降J1随强透水层上游开口长度L1的变化曲线，如图10所示。

图7坝踵处渗透坡降随强透水层厚度的变化曲线 图8出逸坡降随强透水层厚度的变化曲线

图9渗流量随上游开口长度的变化曲线 图10坝踵处渗透坡降随强透水层上游开口长度的变化曲线

由图10可得，各曲线变化规律类似，变化平缓，波动较小；以上游开口长度L1=50 m为对称轴；(1)当L1≤50 m时，坝踵处渗透坡降J1随左端开口长度L1增大而增大，增幅为0%～4.51%；(2)当上游开口长度L1≥50 m时，L1从50 m增大至100 m时，坝踵处渗透坡降J1降低1.19%～2.31%。(3)当防渗墙深度S2=110 m时，为全封闭式防渗墙，对应的J1较小(0.247～0.25)。

当强透水层厚度d=1 m，深度S1=55 m时，作出逸坡降J2的变化曲线如图11所示。

由图11可看出，J2与Q的变化规律类似。出逸坡降J2随强透水层上游开口长度L1的增大而增加，增幅为0.005%～0.2%；且防渗墙深度S2=110 m对应的出逸坡降曲线近似水平，变化幅度最小。

4.3.2 强透水层开口在防渗墙下游 进一步分析渗流量Q和渗透坡降随强透水层下游开口长度L2(下文简称“下游开口长度”)的变化规律，渗流量曲线如图12所示。

由图12可得，各曲线变化规律类似，都以强透水层下游开口长度L2=40 m为对称轴，呈先增大后降低的趋势；当下游开口长度L2由10 m增大至40 m时，渗流量Q增大0～0.71%；当L2由40 m增大至100 m时，渗流量Q降低0.33%～0.59%。且采用全封闭式防渗墙控渗时(S1=110 m)，控渗效果明显优于其他工况。

作坝踵处渗透坡降J1随强透水层下游开口长度L2的变化曲线如图13所示。

对比图12与13可知，两者变化规律类似，以下游开口长度L2=40 m为对称轴，在该处达到极大值；当L2由10 m增大至40 m时，坝踵处渗透坡降J1增大0～2.76%；当L2由40 m增大至100 m时，J1降低0.8%～2.14%。

作出逸坡降J2的变化曲线如图14所示。

图11出逸坡降随强透水层上游开口长度的变化曲线 图12渗流量随强透水层下游开口长度的变化曲线

图13坝踵处渗透坡降随强透水层下游开口长度的变化曲线 图14出逸坡降随强透水层下游开口长度的变化曲线

由图14可得，出逸坡降J2随下游开口长度L2的增加而增大，增幅为0.06%～0.13%；且采用全封闭式防渗墙(S2=110 m)时，J2增大最为显著(0.13%)，其余曲线近似水平。

综上所述，渗流量Q、坝踵处渗透坡降J1、出逸坡降J2曲线变化平缓，可见强透水层下游开口对渗流影响较小。

4.3.3 强透水层开口在防渗墙底端 进一步分析渗流参数随强透水层底端开口长度L3的变化曲线，如图15所示。

由图15可得，渗流量曲线大致分3类，“显著上升曲线”、“平缓上升曲线”、“平缓下降曲线”。(1)当S2=0～50S1=55 m时(防渗墙穿过强透水层)，L3由10 m增加至100 m时，Q增大0.03%～1.05%；(3)当S2=110时，为全封闭式防渗墙，L3由10 m增加至100 m时，Q反而降低0.07%。

作坝踵处渗透坡降J1随底端开口长度L3的变化曲线如图16所示。

由图16可得：(1)当S2=0～50 mS1=55 m时，防渗墙穿过强透水层，L3由10 m增大至100 m时，J1增大0.28%～3.29%；(3)当S2=110 m时，为全封闭式防渗墙，L3由10 m增大至100 m时，J1降低0.4%。

作出逸坡降J2的变化曲线如图17所示。

对比图15～17不难得出，三者变化规律类似，J2的变化规律不再详细赘述。(1)当S2=0～50 mS1=55 m时，J2增大0.02%～0.1%；(3)当S2=110 m时，J2反而降低0.01%。

前文已经详细分析了强透水层上游、下游、底端开口长度对渗流量Q、坝踵处渗透坡降J1、出逸坡降J2的影响规律，但何种开口形式对控渗工程更不利尚不明确，需展开对比分析。

4.3.4 强透水层开口形式分析 以强透水层厚度d=1 m、深度S1=55、开口长度L1=L2=L3=50 m为例，针对强透水层开口形式作对比分析。作不同开口形式下渗流量Q随防渗墙深度S2的变化曲线，如图18所示。

分析图18不难得出，(1)各曲线变化规律类似，渗流量(Q上、Q下、Q底)随着防渗墙深度S2的增加而减小；S2由0 增大至110 m，Q上、Q下、Q底分别降低27.95%、27.68%、28.28%。(2)Q上、Q下、Q底分别为2.738×10-5～3.8×10-5、2.722×10-5～3.764×10-5、2.726×10-5～3.801×10-5m3/s，可见Q下明显低于Q上和Q底，下游开口对渗流量Q影响最小。(3)当S2=0～50 m时，防渗墙未穿过强透水层时，各曲线并未重合；当防渗墙穿过强透水层(S2=0～60 m)时，各曲线近似重合；可见当防渗墙穿过强透水层后，强透水层的开口形式对渗流量影响较小。

当强透水层开口长度L1=L2=L3=50 m时，作坝踵处渗透坡降J1变化曲线如图19所示。

对比图18与19不难得出，渗流量Q曲线和坝踵处渗透坡降J1曲线变化规律类似，其变化规律不再赘述。此外，J1上、J1下、J1底分别为0.25～0.839、0.249～0.827、0.25～0.851，J1底>J1上>J1下，可见对坝踵处渗透坡降影响从大到小排序为：底端、上游、下游。

当强透水层开口长度L1=L2=L3=50 m时，作出逸坡降J2变化曲线如图20所示。

图15渗流量随强透水层底端开口长度的变化曲线 图16坝踵处渗透坡降随底端开口长度的变化曲线

图17出逸坡降随底端开口长度的变化曲线 图18不同开口形式渗流量随防渗墙深度变化曲线

图19不同开口形式坝踵处渗透坡降随防渗墙深度变化曲线 图20不同开口形式出逸坡降随防渗墙深度变化曲线

对比图18～20可得出，Q、J1和J2的规律类似，随着S2的增大而降低。当S2由0增大至110 m时，J2上、J2下和J2底分别降低2.8%、2.7%和2.82%。当S2=0～50 mJ2上>J2下；当防渗墙穿过强透水层时(S2=60～110 m>S1=55 m)，3曲线近似重合。

5 讨 论

5.1 平缓曲线分析

由4.3节可知，在分析强透水层对渗流场的影响规律时，图9～17中渗流参数曲线变化平缓，展开如下讨论。

(1)当防渗墙未穿过强透水层时(S2=0～50 m

(2)当防渗墙穿过强透水层时(S2=60～110 m>S1=55 m)，防渗墙与下层弱透水层(位于强透水层下部)形成封闭式联合防渗体系，强透水层开口长度的改变对渗流参数影响较小。

5.2 防渗墙设置分析

本文深厚覆盖层坝基主要由弱透水层(黏土)构成，局部区域的强透水层为渗流集中通道，为控渗工程中的“薄弱环节”。在分析强透水层特性(S1、d、L1、L2、L3)对各渗流参数的影响时不难得出，当防渗墙穿过强透水层时对应的渗流参数(Q、J1、J2)，明显低于未穿过时对应的各参数；此外，当采用全封闭式防渗墙时(S2=110 m)，渗流参数都降至最低。因此，针对局部区域存在强透水层的深厚覆盖层地基，防渗墙设置时应穿过强透水层，形成相对封闭的联合控渗体系；若仍不能满足控渗要求时，建议做成全封闭式防渗体系。

6 结 论

基于非饱和土渗流理论，探讨深厚覆盖层坝基中局部强透水层特性对渗流场的影响规律，得出以下5点结论。

(1)当强透水层深度大于防渗墙深度时，渗流量、坝踵处渗透坡降和出逸坡降随着强透水层深度增大而减小；反之，随着强透水层深度增大，渗流量逐渐增大，坝踵处渗透坡降先降低后增大，出逸坡降降低。

(2)渗流量、坝踵处渗透坡降、出逸坡降皆随着强透水层厚度的增加而增大；且当防渗墙底端位于强透水层时，渗流参数显著增大。

(3)随着强透水层上游开口长度增大，渗流量和出逸坡降逐渐增大，坝踵处渗透坡降先增大后降低；随着强透水层下游开口长度增大，渗流量和坝踵处渗透坡降先增大后降低，出逸坡降逐渐增大；各渗流参数随强透水层底端开口长度的增加而增大，全封闭式防渗墙除外。

(4)当强透水层处于坝基中间位置，且厚度和开口长度一定时，各渗流参数随防渗墙深度的增加而降低；各开口形式对渗流参数影响从大到小排序为：底端、上游、下游。

(5)针对深厚覆盖层中存在局部强透水层的特殊地基，设置防渗墙时应穿过强透水层，形成相对封闭的联合控渗体系；若仍不能满足控渗要求时，建议做成全封闭式防渗体系。