基于地基承载力的爆炸挤密桩平面间距优化研究

黄晨旭， 李海超， 崔子鑫， 庞 彧

(1.陆军军事交通学院学员第五大队，天津 300161；2.陆军军事交通学院国防交通系，天津 300161)

着眼于应急交通保障、确保战略通道的畅通，具有施工简便、成本低廉、加固深度大等特点的爆炸挤密法在抢建打通断头路、抢修损毁道路和快速提升道路承载能力等方面具有独树一帜的优势。

由于爆炸挤密桩的平面布局影响爆炸挤密法的挤密加固效果，进而影响了加固地区的承载能力，所以对桩的平面布局进行研究具有很重大的现实意义。本文以快速提升未通路段通行能力为背景，运用数值模拟的方法，以桩土复合地基承载力为对象，对黄土地区爆炸挤密桩的平面布局进行研究。

平面布局设计涉及布局形式以及布局间距两方面。在爆炸挤密法桩平面布局形式方面，周双涛等[1]运用LS-DYNA，得到了三点起爆布局形式加固黄土软基效果较好的结论。王鹏[2]研究了不同的爆点布局形式对加固后的黄土软基地区承载能力的影响，得到了在相同置换率的前提下，等边三角形布局明显优于正方形布局的结论。不过，在爆炸挤密桩平面间距方面，目前鲜有研究。董立颖[3]提出了将两个相邻药包爆破后的土体密度显著变化范围重叠1/7作为爆点间距(即爆炸挤密桩间距)，但是该方法并无实际依据，只是根据经验确定，很难说科学、合理。

因此本文针对使用爆炸挤密法施工的黄土填筑路基，炸药采用等边三角形的布局形式，对爆炸挤密桩间距的优化设计展开研究。

1 爆炸挤密规律分析

1.1 爆炸模型的建立

本文的爆炸挤密模型采用ANSYS/LS-DYNA进行数值模拟，计算模型包括炸药和土体2种材料，均采用SOLID164单元。

炸药采用MAT_HIGH_EXPLOSIVE_BURN模型以及JWL平衡方程对施工中常用的2号岩石乳化炸药进行模拟，具体参数及平衡方程设置见文献[4]。根据钻孔设备及工程条件两方面因素，本文采用条形药包。所用炸药的等效半径为2.26 cm，药包长度为190.4 cm，长细比为42.12，重量为4 kg。2号岩石乳化炸药的TNT当量为0.76[5]。本试验计算得到埋深应该不小于289.7 cm[6]，所以在建立模型时炸药上表面距离路基顶面为300 cm。

爆炸模型参考文献[7]建立，如图1、图2所示。由魏连雨[8]研究可知，本文的单点爆炸挤密横向影响范围约为200 cm，所以为研究不同桩间距爆炸挤密规律，共设置桩间距225 cm、250 cm、275 cm、300 cm、325 cm、350 cm、375 cm、400 cm等8个工况。由于桩是由爆炸空腔填筑而成，因此桩间距就是药包的圆心间距。因为模型对称，所以取一半模型进行建模以减少计算时间。

所用黄土材料模型为MAT_SOIL_AND_FOAM模型，实验数据来源于室外试验，具体参数设置为：密度ρ1.85 g/cm3；含水率ω17.10%；泊松比μ0.35；剪切模量G29.6 MPa；体积卸载模量K44.46 MPa；动力屈服函数常数a03.20E+8 Pa2;动力屈服函数常数a17.40E+3 Pa;动力屈服函数常数a2 0.042 7。

图1 爆炸模型尺寸(单位：cm)

图2 爆炸模型

1.2 爆炸挤密规律探究

为了研究炸药对土体的挤密作用，使用LS-PrePost软件对计算结果文件进行提取分析。因为土体在软件中是属于一个PART，所以软件只能以密度等值面的形式展现出爆炸影响范围内的土体密度情况。为方便定量分析炸药对土体的挤密作用，考虑到土体密度变化不大时物理力学性质与参数变化不会特别明显，所以以土体密度1.85 g/cm3为基准、以0.05 g/cm3为间隔，对土体进行分层处理。通过对数据的分析，可以得到以下规律：

(1)由模拟输出的数据可知，爆后空腔两端呈椭球状，中间大致呈圆柱体，爆点附近土体密度等值面大致呈椭球面。在此选取典型工况1、工况5中两爆点连线截面图(如图3所示)。

图3 各工况两爆点连线垂向剖面

(2)当爆腔稳定后，各工况的最大密度值在2.10～2.20 g/cm3之间，总体呈现下降趋势。各工况最大密度值如表1所示。

表1 各工况下土体的最大密度值 g/cm3

(3)通过模拟输出的数据可以明显看出，当桩间距小于等于300 cm时，爆腔周围可以明显看出存在密度为2.05 g/cm3以上的土体层；当桩间距大于300 cm时，爆腔周围土体密度为2.05 g/cm3以上的土体层体积小且分散，不能连接成一个整体。因此在数据处理时，工况5～工况8不考虑建立密度为2.05 g/cm3以上的土体层。将各工况爆腔周围不同土层数据提取后通过建模软件SolidWorks建模后，得到各层土体体积如表2所示。

表2 各工况爆腔周围不同土层体积 cm3

通过表2可以看到，就加固后的土体密度而言，当爆点间距越近，爆腔周围土密度呈现增大的趋势，加固效果稍好。但是，就加固后的土体密度显著变化范围而言，在本文研究的8个工况中，不同工况的土体密度显著变化体积相差不超过5%，所以桩间距的不同对爆腔周围土体的加固效果有影响，但是不明显。这是因为各工况的桩间距明显大于单个药包的横向影响范围，所以不同的桩间距对桩周土的影响较小。

(4)通过不同工况的垂向剖面图(见图4)，桩间距对加固区域的影响主要体现在等边三角形的形心附近的土体加固程度上。桩间距越小，等边三角形形心区域爆后土体密度越高，土体密度显著变化的体积越大。这是因为桩间土受两侧爆点的爆炸冲击波共同影响，因此桩间土的挤密效果受桩间距的影响较大。

图4 不同工况模型的垂向剖面

(5)观察过两爆心的横截面(见图5)，可以看出当桩间距较小时，两爆点连线方向上爆腔有所变形。这意味着，如果爆点间距过小的话，炸药的能量多用于挤密土体，但是却减弱了成腔作用。这是造成爆腔变形的原因。

图5 工况3横截面(图中点为药包圆心坐标)

2 承载力计算

2.1 建模说明

由于爆后土体密度变化明显，无法将其视为同种性质的土体，同时目前没有任何办法能将LS-DYNA的计算结果文件直接导入到任何静力学分析软件中。为了能够计算出爆后复合地基承载力特征值，需要对模型进行合理的处理。

(1)将土体按照密度等值线图进行分层建模得到的椭球形土体模型非线性程度太高，计算难以收敛。为了达到既收敛又与实际相符合的目的，因此在体积相等的前提下，将分层的土体转化成圆柱体进行建模。

(2)在工程中应用爆炸挤密技术将使用群桩对土体进行加固，本文受条件所限，只选取其中一个基本单元进行研究。由规范[9]可知，复合地基静荷载试验测定的是承压板下复合土层的承载力。为了计算出群桩条件下两桩间土体的承载力特征值，承压板只作用在桩中心线围成的部分桩以及桩间土体上。因此承压板为边长为桩间距的等边三角形，厚度为10 cm。整体模型以工况6为例，其承载力计算模型如图6所示。

图6 承载力计算模型

(3)各层土体之间采用绑定接触使之成为一个整体。碎石桩的摩擦系数通常取为0.2，为模拟桩土间的摩擦接触，接触的材料属性为：切向接触为系数取0.2的“罚函数”，法向接触为“硬接触”。在对称面上施加对称约束边界条件，在底面施加固定约束边界条件。

(4)因为各个工况的土层的大致形状是类似的，但是模型各个PART形状不同。因此根据PART的不同形状选用结构化网格、扫略网格或者是自由网格划分技术来对各PART进行划分，以达到减少网格畸变、便于计算收敛的目的。同时加密桩土结合部分的网格，提高计算精度。

(5)荷载沉降曲线的获得方法有2种，分别是给定荷载求解位移或者是给定位移求解对应荷载。为了避免达到极限条件、刚度减小带来的收敛问题，本文采用第2种方法，即在承压板表面施加向下的位移约束，求解对应荷载值。

(6)由于爆炸作用时间较短，土中水难以完全排出，故假设土体的含水率取恒定值，不考虑桩体的排水固结作用。

2.2 确定试验参数

承压板所用钢材料密度为7.85 g/cm3，弹性模量为200 GPa，泊松比为0.35。根据文献[10]桩体采用级配碎石，因此可以采用线弹性模型，密度为2.5 g/cm3，弹性模量为250 MPa，泊松比为0.3。

因为Mohr-Coulomb(摩尔-库仑)模型主要适用于单调荷载下的颗粒状材料，所以本文黄土采用ABAQUS材料库中的线弹性模型和Mohr-Coulomb模型进行模拟，实验数据来源于室外试验，具体黄土模型参数设置如表3所示。

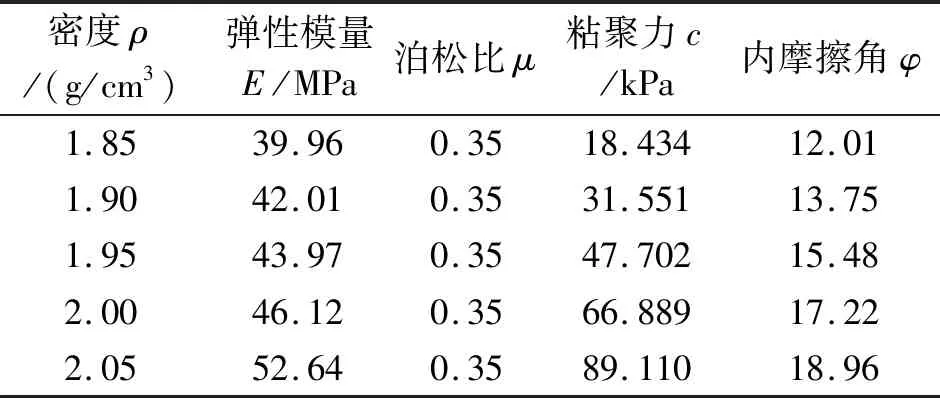
表3 土壤模型参数

2.3 计算结果及分析

根据规范[11]的要求，取沉降s与承压板边长b之比为0.01时的压力值为复合地基承载力特征值。各工况的复合地基承载力特征值如表4所示。

表4 各工况的复合地基承载力特征值 kPa

表4数据经过MATLAB以95%的置信度进行拟合，得到复合地基承载力特征值P(kPa)与桩间距L(cm)之间的关系式为：

P=2.309×10-5L3-0.019 97L2+4.983L-76.13

(1)

其中，该拟合曲线的确定系数R2=0.997 6。

通过对承载力数据的分析，在本文选取的桩间距2.25～4 m的情况下，桩间距越小时，复合地基承载力特征值越大，且桩间距与复合地基承载力特征值呈现较好的三次曲线关系。

3 桩间距优化

从计算结果可以看出，当桩间距小时，桩的布置较为紧密，加固区域的复合地基承载力较高，但是施工成本增加，同时也会影响爆后成腔效果，没有充分利用炸药能量；当桩间距大时，加固区域的复合地基承载力不足，道路容易发生各种病害，因此需要对桩间距进行优化设计，以便选择合理的桩间距。因此，目前需要建立一个地基承载力的基准，当加固地区的地基承载力满足该基准后，尽量选用较大的桩间距，以达到兼顾加固效果与施工成本的目的。

3.1 复合地基承载力基准

爆炸挤密桩法加固后的路基顶面主要承受着路面结构自重应力σB以及车轮荷载产生的附加应力σZ。合理的设计思路应为路基顶面所受的总应力在路基土的弹性限度范围内，即路基土的地基承载力特征值应该大于路基土表面所受垂直应力σS。在这种情况下，当车辆驶过后，路基土能够恢复原状，以此保证了公路的相对稳定，大大降低了路面发生各种病害的概率。所以将路基顶面所受的总应力作为加固后的复合地基承载力的基准，以此来选取合理的桩间距。

加固后路基土表面的垂直总应力σS为

σS=σB+σZ

(2)

其中车轮荷载的大小即轮胎接地压力p(kPa)可由文献[12]中给出的单轴轴载Ps(kN)和轮胎内压Pi(MPa)的经验公式得出。

p=0.0021Ps+0.29Pi+0.145

(3)

轮胎与地面的接触面轮廓大致为一个椭圆形，因其长轴短轴差别不大，所以可以将车轮荷载简化为当量的圆形均布荷载。当量圆半径δ(m)可由路基路面工程[13]中的公式(4)确定：

(4)

式中：P为作用在车轮上的荷载(kN)。

公路由路面和路基两部分构成。公式(3)得到的是车轮荷载在路面的接触压力。为了得到车轮荷载在路基土表面的垂直应力σZ，由土力学[14]可知，当地表圆形面积上作用竖直均布荷载p时，在荷载中心O处下任意深度z处M点的竖直附加应力σZ，可以由布辛内斯克解在圆形面积内进行积分得到。

所以，在整个圆形面积上的均布荷载对于圆心下任意深度z点的附加应力σZ应为公式(5)所示：

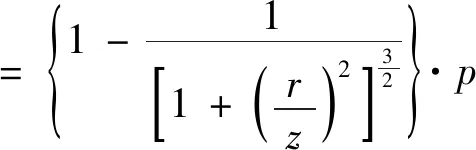
(5)

式中：r为圆面积半径，即车辆荷载的当量圆半径，r=δ；ρ为均布荷载作用范围的极径，0≤ρ≤r；θ为均布荷载作用范围的极角，0≤θ≤2π。

显而易见，在同一水平面内，在圆形竖直均布荷载p作用下，荷载中心O处的竖直附加应力σZ是最大的。因此，选取O处的竖直附加应力作为同一深度路基受力的控制值。

而路面自重在路基顶面所引起的垂直压应力σB按式(6)计算：

σB=∑γiZi

(6)

式中：γi为第i层路面的重度；Zi为第i层路面的厚度。

3.2 桩间距优化设计

为达到应急交通保障的目的，快速提升未通路段通行能力，在对路基使用爆炸挤密法施工加固后，路面铺设15 cm的水泥稳定级配碎石作为临时路面。为了能够确定爆炸挤密桩的合理间距，在这里按照规范[15]的要求，车辆荷载取100 kN，Ps=0.7 MPa，当量圆直径δ=0.213 m，由公式(3)可知轮胎接地压力p=558 kPa。水泥稳定级配碎石路面的重度γ=25 kN/m3。路面自重在路基顶面所引起的垂直压应力以及车辆荷载在路基顶面的附加应力的计算深度都取路基顶面距路面表面深度Z=15 cm。所以根据公式(2)、公式(4)～公式(6)以及路面的实际情况，该路段路基顶面所受的垂直总应力，即复合地基承载力基准σs=259.25 kPa。由拟合公式(1)以及承载力基准可知合理的爆炸挤密桩间距应该是L=281.4 cm。为了方便具体施工，爆炸挤密桩间距取L=280 cm。

4 结束语

(1)当桩间距大于单桩横向影响范围且小于两个影响范围之和时，桩间距对桩周土的挤密效果影响较小，但是对桩间土的挤密效果影响较大。

(2)在桩间距2.25～4 m的情况下，桩间距越小时，路基的承载力特征值越大，且桩间距与承载力特征值呈现较好的三次曲线关系。

(3)爆炸挤密技术处理后的路基承载力受炸药、土体、桩体等多因素共同影响。本文模型在爆炸挤密桩间距L=280 cm时，即使只铺设了15 cm厚的水泥稳定级配碎石作为临时路面，也足以满足行车需求。该方法可以为下一步进行桩间距影响因素分析奠定基础，进而为研究爆炸挤密桩具体布局设计方案提供参考与借鉴。