带粘性的层次Dirichlet过程聚类方法
李 涵,张 娜
(深圳大学 经济学院,广东 深圳 518060)
一、引言
聚类分析是挖掘数据信息的一种方式,其目的是把一个有限的、未标记的数据集,根据预定义的相似性度量,划分成多个自然的类别,从而使得来自同一类里的数据对象都彼此接近,不同的类中的数据对象彼此不同[1]。聚类分析是模式识别的一个相关工具,在许多领域都有应用,如生物信息学、信息检索、市场研究、股票趋势分析等。
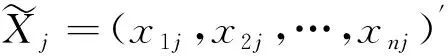
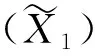

二、Sticky HDP模型的相关理论
(一) 模型介绍
1.Dirichlet过程
Dirichlet过程是一个应用在非参数贝叶斯模型中的随机过程,根据Ferguson的研究成果[8],Dirichlet过程的定义如下:假设H是测度空间Θ上的随机概率分布,对于测度空间Θ的任意一个有限划分A1,A2,…,Ar,如果测度空间Θ上的随机概率分布G满足以下条件:
(G(A1),(G(A2),…,G(Ar))~Dir(αH(A1),αH(A2),…,αH(Ar))
(1)
则G服从以H和α为参数的Dirichlet过程,记为G~DP(α,H)。其中,H为基分布,α>0,为集中度参数,表示了基分布H和G的相似程度。α越大,两者越相似。
以上为Dirichlet过程的定义,为了实现Dirichlet过程的抽样,研究者们提出了三种等价形式来构造Dirichlet过程,分别为Blackwell-MacQueen urn scheme、Chinese restaurant process和stick-breaking构造[9-11]。本文主要应用的是其中的stick-breaking构造形式, 随机概率分布G的生成过程如下。
k=1,2,…
(2)

2.Dirichlet过程混合模型
Dirichlet过程混合模型在Dirichlet过程上进行了扩展[4],对模型参数用Dirichlet过程作为其先验分布。假设有独立观测数据{y1,y2,…,yn},引入指示因子{z1,z2,…,zn},其中指示因子zi表示观测数据yi的类别标签,θzi表示在类别标签zi下,观测数据yi服从分布F(θi),则观测数据yi(i=1,2,…,n)的生成过程如下:
k=1,2,…
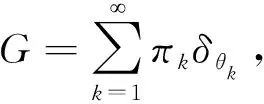
(3)
Dirichlet过程混合模型是有限混合模型的推广,区别在于其类别个数是无限的,把{z1,z2,…,zn}通过求和的形式去掉,得到如下形式:
f(y1,y2,…,yn∣θ1,θ2,…,θk,…)

+πkF(yi∣θk)+…]
3.Sticky HDP模型及其应用
层次Dirichlet过程是Dirichlet过程的推广[12],其形式为:G0|γ,H~DP(γ,H),Gj|α,G0~DP(α,G0)。其中,H是基分布,γ和α是集中度参数。本文提出的带粘性的层次Dirichlet过程(sticky HDP)基于Fox、Sudderth和Jordan等提出的sticky HDP-HMM过程[13]。Sticky HDP-HMM是在层次Dirichlet过程隐马尔科夫模型(hierarchical Dirichlet process hidden Markov model,HDP-HMM)的基础上,用粘性来反映自身状态的滞留。本文在此基础上做了如下改进:用sticky粘性反映总体聚类和指标数据聚类的相似性;允许不同的状态取不同的分布类型,即不同的指标服从不同的分布。
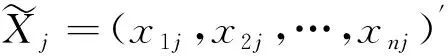
这里K设为分类数目的上限,一般情况下根据观测对象的个数设定,并不需要知道准确的分类数目,最终的分类数目依赖于观测数据[13]。
πj|αj,zi=k~Dir(αjβ1,…,αjβk-1,αjβk+κj,αjβk+1,…,αjβK)
(4)

(二)参数推断
本文用马尔科夫链蒙特卡罗方法(MCMC)中的Gibbs抽样算法来实现参数的推断[14]。Gibbs抽样算法主要分为Polya Urn Gibbs抽样和Blocked Gibbs抽样,但是前者的收敛速度比后者慢[15]。所以,本文对于各指标数据采取的是Blocked Gibbs抽样算法来推断参数及实现聚类。
本文在分析时不限定Fj(·)的分布类型,以下的标记符号和前文保持一致。
1.各参数的先验分布
参数αj+κj和αj的先验分布。参数αj+κj的先验分布为:αj+κj~Gamma(a,b),参数αj的先验分布与αj+κj属于同一分布族[16]。
2.各参数的后验分布
给定参数的先验分布和观测数据服从sticky HDP模型,根据贝叶斯公式,可得到各参数的后验分布,分别如下。

δ(τij,k) 。

3)参数β的后验分布。参数β的后验分布为:(β1,β2,…,βK)~Dir(γ/K+n1,…,γ/K+nK),其中,nk表示总体观测数据中属于类别k的个数。
4)参数πj的后验分布。参数πj的后验分布为:πj∣τj,zi=k~Dir(αjβ1+mj1,…,αjβk-1+mjk-1,αjβk+κj+mjk,αjβk+1+mjk+1,…,αjβK+mjK),其中,mjk表示在总体聚类属于第k类的各数据Xi中,其对应的各指标数据xij在指标数据的聚类中属于第k类的个数。
5)参数αj+κj的后验分布。参数αj+κj的后验分布为[16]:p(αj+κj∣Kj,n,ω)∝(αj+κj)a+Kj-1e-(αj+κj)(b-log(ω))+n(αj+κj)a+Kj-2e-(αj+κj)(b-log (ω)),其中,ω为辅助变量,ω~Beta(αj+κj+1,n)。参数γ的推断与αj+κj相似,可以参考αj+κj的推断过程。

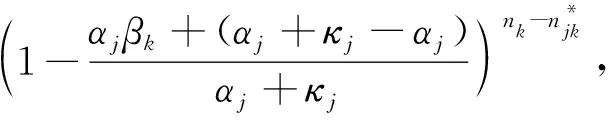
三、仿真模拟结果与分析
为了验证本文所描述的用sticky HDP模型对由多个指标组成的多元数据进行聚类的有效性,分别对仿真模拟数据和IRIS数据集进行了聚类分析。在进行聚类时,运行Gibbs抽样迭代1 500次,由于仿真模拟数据的参数在300次左右达到平稳,IRIS数据集的参数在200次左右达到平稳,故都取前500次作为预热抽样数目,然后在500~1 500次迭代中,每间隔5次迭代保留一次参数样本,选取出现概率最大的类别个数作为最终类别个数,然后选取该类别个数下极大似然函数值对应的分类结果作为总体数据最终的聚类结果。对于仿真模拟数据,在模型的初始设置中,对聚类类别的上限个数尝试了多个数值,分别有K=20,25,30等。结果显示该初始设置足够大时,对参数估计和最终的总体分类结果没有影响。
对于仿真模拟数据和IRIS数据集,真实的类别已知。本文将分别运用不同的聚类方法对数据集进行聚类分析,以分类的准确率作为标准来判断不同聚类方法的优劣。其中,对于模拟数据,所有的运行结果都是基于30次运行结果的平均值,而结果后面括号里的数值是标准差。
本文运行算法的计算机硬件配置如下:Inter(R)Core(TM)i5-5200U CPU@2.20 GHz,8G内存;操作系统为Windows 10;程序运行软件环境:R 3.5.0。
(一)仿真模拟数据

表1 各指标数据中各成分模型对应参数

表2 各指标数据参数的先验分布

表3 各超参数的先验分布
为了验证指标数据粘性大小对于模型最终聚类结果准确率的影响,在生成数据时,设置了多组不同的粘性参数,如表4所示。其中第四组数据粘性参数的设置,是为了验证当各个指标数据的粘性大小不同时,对最终聚类结果准确率的影响,即检验模型的稳健性。模拟数据聚类结果的准确率见表4。其中,准确率定义为样本分类结果与其真实分类一致的比例。

表4 总体数据聚类结果
从表4可以看出,指标数据的粘性越大,总体数据聚类结果的准确率越高。当指标数据的粘性有高有低,如表4中的第四组总体数据,指标数据中粘性最大的有0.8,最小的仅0.1,而最终聚类结果的准确率为85.21%(见表4中*1处),这说明了sticky HDP模型的稳健性,即当指标数据中有粘性很小的数据时,对sticky HDP模型聚类的准确率影响不大。当指标数据的粘性都较小,仅0.4时,总体数据聚类结果的准确率骤降,从粘性0.5时的54.58%下降到32.51%(见表4中*2处),说明当指标数据的粘性低于0.5时,即指标数据与总体数据聚类之间的相关性都较弱时,总体聚类的精度较差。当指标数据都没有粘性,即粘性为0时(见表4中*3处),总体聚类和指标数据聚类相互独立,该准确率为简单随机情况下的结果。
同时,分别运用K-均值聚类方法、最短距离法和最长距离法对该仿真模拟数据进行聚类分析,聚类对比结果见表5。其中各模拟组别的指标数据粘性大小设置与表4一致,K-均值聚类方法和系统聚类法的聚类个数均设为真实值10。
根据表5的结果,以准确率为标准,四种聚类方法的优劣次序依次是sticky HDP聚类方法、K-均值聚类方法、最长距离聚类法以及最短距离聚类法。其中,当指标数据的粘性较大时,sticky HDP聚类方法的准确率明显高于其他方法,显著提高了分类质量。同时,sticky HDP聚类方法还不需要事先知道确切的分类数目,均证实了用该模型对多元数据进行聚类的有效性。

表5 不同聚类方法的聚类结果(基于准确率)
(二)IRIS数据集
本文以经典的IRIS数据集作为测试数据集。该数据集是从加拿大加斯帕半岛上鸢尾花的花朵中提取的地理变异数据,其中包含150个鸢尾花花朵样本,分属于鸢尾花下的3个类别,分别是山鸢尾、变色鸢尾和维吉尼亚鸢尾。每个类别中有50个样本,每个样本包含鸢尾花的花萼和花瓣的长度及宽度4个特征属性,即萼片长度(Sepal Length)、萼片宽度(Sepal Width)、花瓣长度(Petal Length)、花瓣宽度(Petal Width)。
在sticky HDP算法的初始化中,聚类的类别个数设置为K=15。最终的聚类结果见表6。

表6 基于sticky HDP模型的鸢尾花数据聚类结果
根据表6的结果,sticky HDP聚类方法能够确定鸢尾花数据的真实类别个数,且能保证准确率,准确率达到92.67%。同时,分别运用基于K-均值聚类方法、最短距离法、最长距离法以及Dirichlet过程聚类方法对该数据集进行聚类分析,聚类对比结果见表7。其中,K-均值聚类方法、最短距离法和最长距离法的聚类个数均设为真实值3。

表7 不同聚类方法的聚类结果
由表7可以看出,以准确率为标准,几种聚类方法的优劣次序依次是sticky HDP聚类方法、K-均值聚类方法、最长距离法、Dirichlet过程聚类方法和最短距离法。其中,sticky HDP聚类方法的准确率高达92.67%,比准确率最低的最短距离法的准确率高出24.67%。由于IRIS数据集中各特征数据处于不同类别时重叠较少,所以K-均值和最长距离法在这种情况下比较适用,但sticky HDP方法仍得到更高的聚类准确率,并且不需要事先知道确切的分类数目,这都证实了用该模型对IRIS数据集进行聚类的有效性。


表8 鸢尾花的特征属性数据的一致性与粘性结果
从表8的结果可以看出,特征属性花瓣宽度的粘性最大,有0.803,这说明该指标与鸢尾花类别的相关性很高,即当该指标中的数据在指标数据的聚类中属于某一类时,其在总体聚类中也属于该类的概率很大(有0.817),根据该指标数据的类别能够在很大程度上判断鸢尾花的类别。而特征属性萼片宽度的粘性最小,仅0.329,这说明该指标与鸢尾花类别之间的相关性很弱,即当该指标中的数据在指标数据的聚类中属于某一类时,其在总体聚类中也属于该类的概率不大(仅0.382),也就是说根据该指标判断鸢尾花类别的准确率很低。
最后,对该数据集下每个特征属性的数据进行直观分析,来进一步验证该聚类方法的结果,每个特征属性数据的直方图见图1。从该直方图可以看出,特征属性中花瓣宽度的数据可能来自三个分布的混合,即有三个类别,这与该数据集下鸢尾花类别的数目一致,则该指标数据的粘性可能较大;而萼片宽度数据可能只来自一个分布,这与该数据集下鸢尾花类别的数目相差较大,则该指标数据的粘性可能较小。该直观分析与表8中估计的粘性结果一致,进一步证实了sticky HDP聚类方法的有效性。

图1 4个特征属性数据的直方图
四、结论
多元数据的各指标服从的分布不同以及相关性的差异会影响聚类方法的适用性、复杂性和准确率。本文提出改进的sticky HDP模型,旨在解决指标服从不同分布的问题,实现多元数据的降维聚类,同时用模型参数来反映指标数据与总体聚类之间的相关性,最后用仿真模拟数据和实例证明了该方法的有效性。指标数据粘性的大小,可以直接反映指标数据与总体数据聚类之间的相关性程度高低。指标与总体聚类的相关性越大,则相应的粘性参数越大,从而反映该指标在总体聚类中的重要性程度越高,这为研究多元数据的聚类、各指标与总体聚类之间的相关性提供了一个新的方法和角度。当各指标数据中有粘性较大的指标时,sticky HDP聚类方法明显优于其他聚类方法,能够显著提高分类质量。而当指标数据与总体数据聚类之间的粘性都很小,即分类的相关性都很弱时,对总体数据进行聚类的意义并不大。 对于仿真模拟数据,sticky HDP算法运行的总时间为0.82h,每次Gibbs抽样过程的平均运行时间为1.96s;对于IRIS数据集,sticky HDP算法运行的总时间为3.78min,每次Gibbs抽样过程的平均运行时间为0.15s。本文的实例只分析了IRIS数据集,后续还可以把这个方法应用到其他领域的数据集上,以进行进一步的挖掘,得到更多有用的信息。

