基于姿态角的轮腿机器人驱动控制系统研究

(东南大学 仪器科学与工程学院，江苏 南京 210096)

移动机器人作为机器人领域的重要分支，可在地震、核辐射及火灾等复杂恶劣环境中代替人类进行探索和作业，具有广阔的应用前景[1]。其中轮腿型机器人同时具有攀爬能力强和操控简单的特征，完全可以胜任城市环境下尤其是攀爬楼梯等工作[2]。且已有研究表明，五星形轮腿结构同时兼顾了机器人的越障能力和速度等性能[3]。

图1中的机器人为本项目组团队研制的五星形轮腿结构机器人，其结构紧凑，尺寸适中，装配有一个四自由度机械手，可实现在城市复杂危险环境中探索作业，尤其适合攀爬楼梯等复杂任务。该轮腿机器人的各项结构参数、质量参数和机电性能如表1所示。

但是在该类轮腿机器人通过楼梯时，往往会因轮腿的相位角差异、摩擦打滑、轮腿磨损等因素导致轮腿机器人在攀爬过程中产生大幅偏移[4]。例如图1中，由相位角差异导致左前轮腿和右前轮腿的主受力腿分别踏在上下两层不同的楼梯上，因为机器人机体较大，较小的偏航角也会导致机器人在楼梯上产生较大的偏移，即增大了机器人不稳定性，容易造成机器人倾翻。同时由于远程无线传输的时延和操控者反应滞后等因素，极易造成机器人偏航角度增大，进而碰撞到左右墙壁。图2为远程遥操作机器人时机器人姿态传感器传回的偏航角和俯仰角的变化图形，图中浅灰色曲线为机器人在爬楼前标定初始数值后计算所得的偏航角，可以用于实时反馈机器人的偏航程度。所以在操控者遥操作机器人攀爬楼梯时，可利用偏航角的姿态实时调整机器人。

图1 轮腿机器人攀爬楼梯照片

项目参数机器人尺寸外形尺寸(含轮腿)(长/宽/高)/mm980/670/340轮距(前后/左右)/mm614/630整备质量/kg40轮子外围直径/mm380电机性能控制模式速度模式额定转速/r·min-155额定扭矩/N·m22.3爬楼转速/r·min-112

图2 攀爬楼梯过程中姿态曲线图

为实现基于姿态角对轮腿机器人进行控制，快速、低成本地开发出机器人闭环控制系统。拟采用基于建模与仿真的虚拟样机技术对机械和控制系统进行联合分析，即通过仿真软件ADAMS 和Simulink建立轮腿机器人虚拟样机的联合仿真，并对整体特性进行反复的仿真测试，减少实际机器人调试的时间[5]。为验证机器人攀爬楼梯时的稳定性，采用重心投影法，分析了机器人攀爬过程中的稳定性能。

1 基于姿态的轮腿机器人驱动控制

1.1 机器人驱动控制目标

轮腿机器人在攀爬楼梯前进过程中，4个轮腿的相位角度等状况不可能绝对同步，所以在其攀爬楼梯过程中，偏航角始终处于一定范围内变动。本驱动控制系统的设计目标是防止前侧左右2个轮腿出现图1中分别跨越上下2层台阶而导致机器人出现较大偏航。图3所示为测得的机器人前侧左右2个轮腿分别跨越2层台阶和同处于1层台阶下的各3次的偏航角。

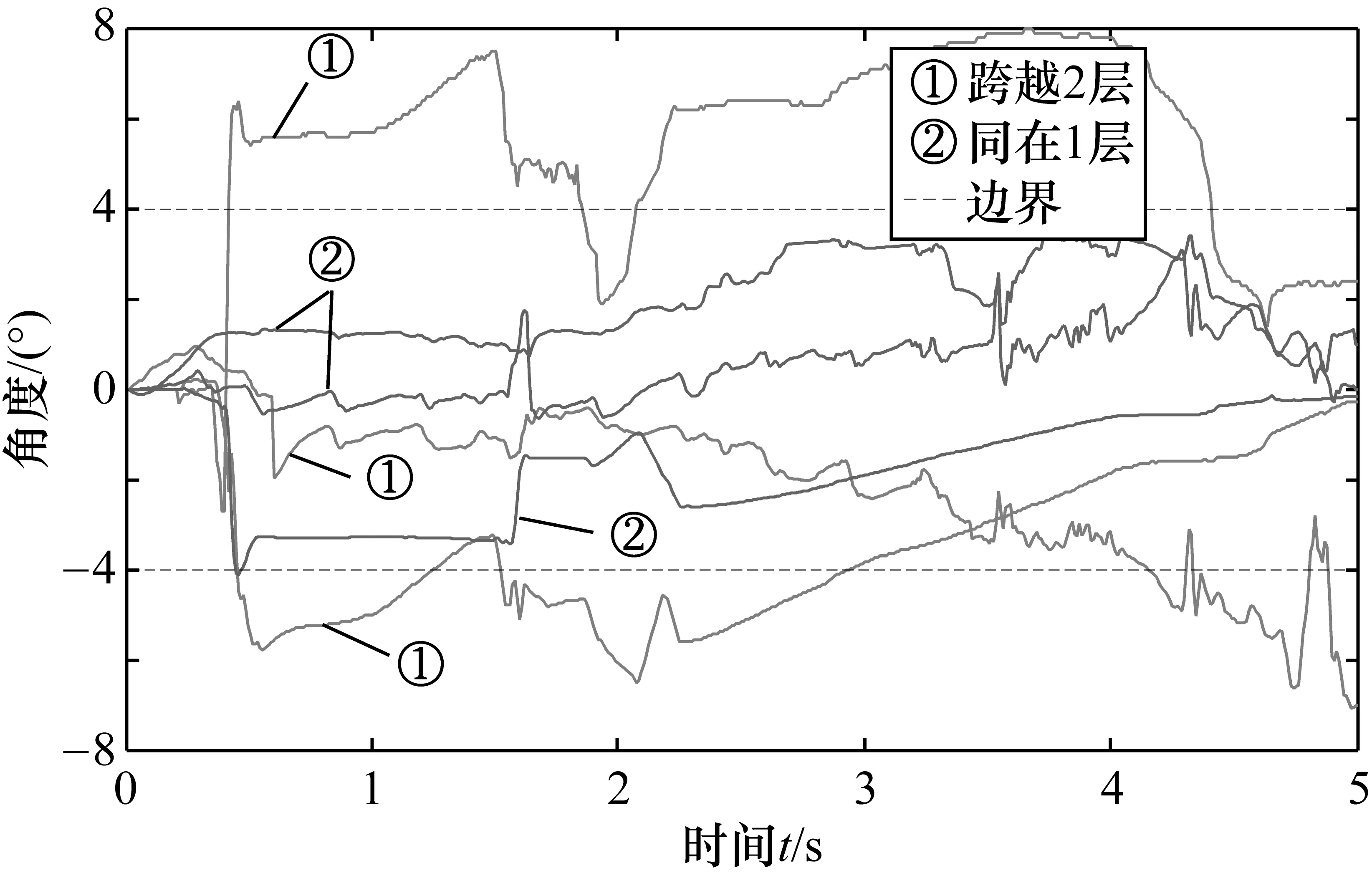
图3 攀爬楼梯过程中姿态曲线图

由图3中两种情况下各3次的偏航角的情况可知，前侧左右2个轮腿同处于1层台阶时的偏航角约在4°包络线内。左右2个轮腿跨越2层台阶时的偏航角会超过5°，所以选用5°为此次仿真中是否进行偏航控制的判断依据。

1.2 机器人动力学建模

通过SOLIDWORKS建立五星形轮腿机器人和楼梯的三维模型。本仿真设置一旦出现5°偏航角时就对机器人的姿态开始调整，所以仿真模型中直接设置机器人初始位置有5°的偏航角。为简化在ADAMS/Simulink联合仿真软件中操作并降低计算量，对实际模型进行适当简化，其中机器人搭载的机械臂和内部的电机、驱动控制器等均简化成等重量、同重心的立方体重块置于机器人机体内，轮腿机器人采用4个独立的减速电机单独驱动。楼梯模型根据GB 50352-2005民用建筑设计通则[6]，设置宽度为28 mm，高度设为18 mm。将SOLIDWORKS中的三维模型导入ADAMS/VIEW中模型如图4所示。

图4 轮腿机器人ADAMS/VIEW模型

将三维模型导入后，为系统添加相关的载荷和约束，其中除了4个轮腿的旋转副外，还添加了机器人可转动腰部关节的旋转副。再分别设置左侧两路电机和右侧两路电机的转速为2个输入变量；设置楼梯重心为基准，测量机器人重心的偏航角YAW变量为输出变量。

1.3 联合仿真模型

利用ADAMS/Control 模块，可以将机械系统仿真分析工具与控制设计仿真软件Matlab有机地连接起来，实现以下功能：

① 把复杂的控制加到ADAMS模型上，可以一次仿真整个系统，遇到问题，可从机械系统和控制系统协调的角度来解决[7]。

② 直接从ADAMS模型中产生机械系统仿真模型，而不用推导，列写较复杂的方程描述机械系统，大大简化了建模过程[8]。

③ 分析在ADAMS环境或者控制应用程序环境获得的联合仿真结果[9]。

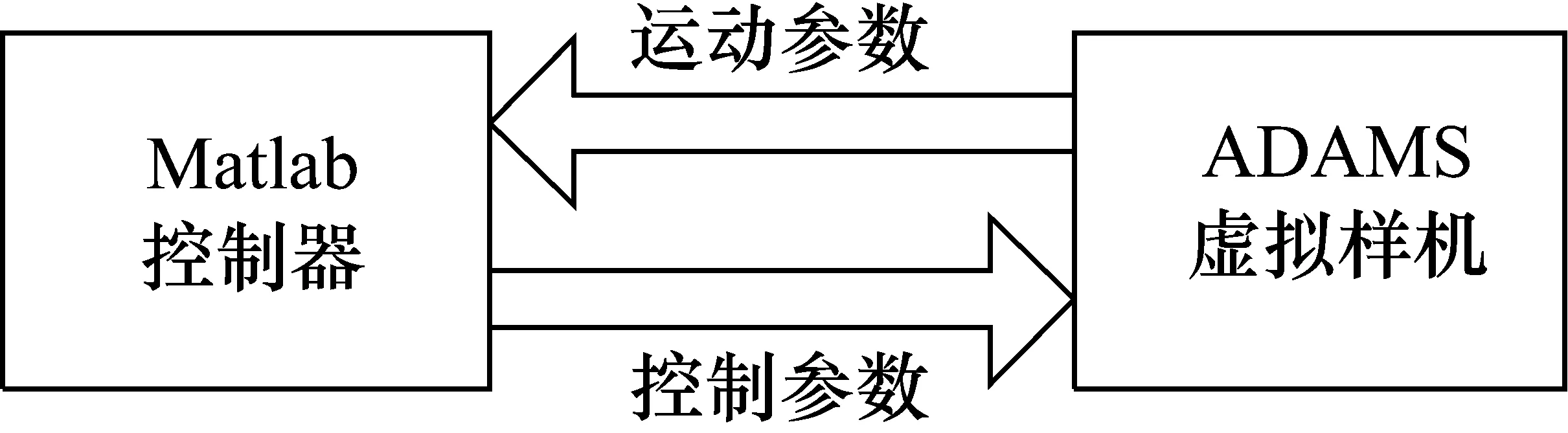
图5 ADAMS/Matlab联合仿真数据交换

在Matlab的Simulink中建立以偏航角YAW为误差，对左右两侧电机转速采用PID驱动控制系统，其中PID模块用于减小误差，抑制超调[10]，限幅模块限制电机转速范围。因为本系统是在出现大偏航后才进行速度控制的，所以系统始终保持初始输入转速72°/s，仿真框图如图6所示。

图6 Simulink仿真框图

1.4 联合仿真结果分析

设置本次控制目标误差小于1°，稳定时间小于2 s。经过反复对PID模块3个系数的调试，最终设置比例系数P=5，积分系数I=0.2，微分系数D=0，经PID驱动控制系统调整的偏航角YAW变化曲线如图7所示。

该仿真表明，基于姿态角的机器人速度PID控制模型可以实现轮腿机器人在出现较大偏航角后，快速调整机器人姿态。

1.5 机器人驱动控制系统

将基于机器人的姿态的驱动控制系统添加于原来的机器人控制系统内，原机器人下层控制系统框图如图8所示。

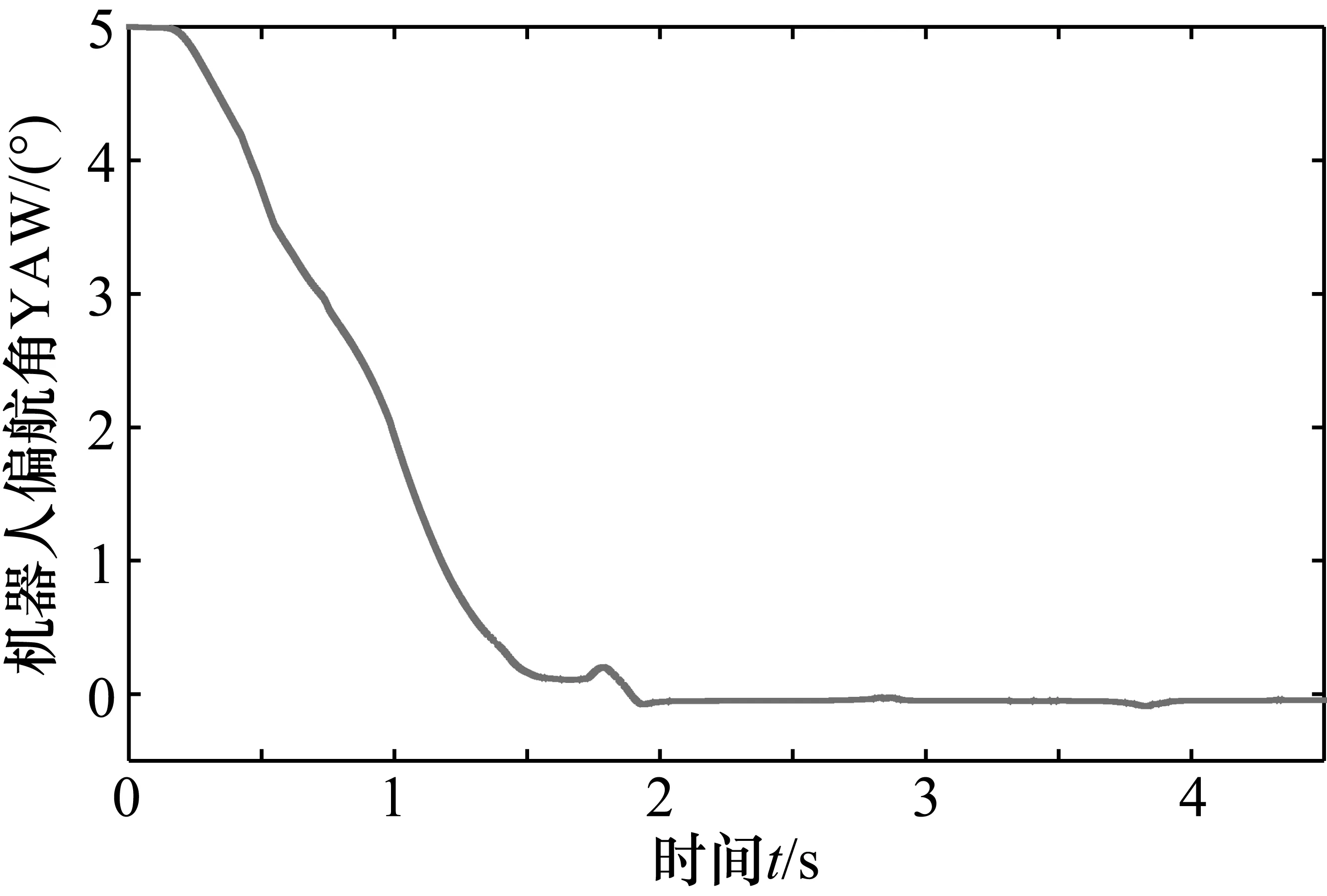
图7 联合仿真调整后机器人偏航角变化曲线

图8 轮腿机器人下位机控制系统框图

其中姿态传感器采用的是整合了6轴运动处理组件的MPU6050，原始的ADC数据从传感器读取后，经过姿态解算，可获得目标载体的俯仰角、滚转角和航向角等数据，测量精度为0.1°。由于传感器在不同的地点采集到的航向角均不同，所以需对航向角先进行一段时间的采集并做归一化求均值后，作为是否偏航的基准值，该任务可由传感器控制模块完成，一旦检测到超过5°，再向主控制器发送偏航角度。主控制对机器人机体运动控制的流程图如图9所示。

图9 下位机主控制器软件流程图

2 轮腿机器人攀爬楼梯稳定性验证

在轮腿机器人攀爬楼梯时，除了需要通过对姿态角的监测进而控制电机，防止偏航角进一步变大，还需要对机器人的稳定性进行验证，防止轮腿机器人在攀爬楼梯时倾翻。

机器人的稳定性能分析一般分为静态和动态两种，其中静态稳定性分析有：重心投影法、静态稳定边界法、能量稳定边界法等[11]。本机器人在攀爬楼梯过程中比正常行走的速度慢，所以仅采取静态分析。童俊华[12]等人通过以判定机器人重力线是否越过倾覆线为标准，通过基于图形的计算来判断。轮腿机器人攀爬楼梯示意图如图10所示，由该图给出轮腿机器人不发生倾翻的条件公式为

(h+Rsinφ)sinθ<(L-Rcosφ)cosθ

(1)

式中，h为机器人重心到轮腿中心的距离；R为轮腿中心至轮腿与地面接触质点的距离；L为重心到两后轮腿中心线法向距离；θ为机器人俯仰角；φ为轮腿与地面接触点与机器人平面的夹角。

图10 轮腿机器人攀爬楼梯倾翻示意图

为保证轮腿机器人在攀爬楼梯过程中遇到极限情况也不倾翻，可将式(1)变换为式(2)。

(2)

由图2中机器人PITCH俯仰角等变化情况可知

(3)

将轮腿机器人的参数L=365 mm，h=25 mm，Rmax=200 mm带入式(2)中，可知该不等式在机器人攀爬楼梯过程中成立，即本轮腿机器人在极限特殊情况下也能满足较高的稳定性能，满足攀爬楼梯等复杂城市环境的需求。

3 结束语

通过ADAMS和Simulink对五星形轮腿机器人的联合仿真，基于实时获取的偏航角角度，利用PID控制器对机器人左右两侧的电机分别调控。直接将该驱动控制系统移植进原机器人控制系统中，该控制系统可以减少机器人在攀爬楼梯过程中出现大偏航的情况，有效防止机器人碰撞上左右两侧的墙壁。利用虚拟样机设计方法，可极大降低研发成本，加快开发进度[13]。本文还借助重心投影法，利用图形化计算确定了轮腿机器人在本驱动控制系统下，即使在极限特殊情况下，同样能保持稳定不倾翻的性能。