基于博弈论的大型活动安全费用投入研究

北京交通大学经管学院 交通大学安全风险管理研究所 王雨情

澳门科技大学商学院 李笑然

随着生产力的不断提高，人类物质生活水平不断改善，精神追求也越来越多，随之而来的是不断增多的大型活动。这些大型活动除了带给我们身心上的欢愉和精神上的享受之外，也带来了数量众多的安全事故，造成大量人员伤亡，令人触目惊心。我国近年举办的大型活动中发生的最轰动世界的安全事故当属“12.31上海外滩踩踏事件”，该事故造成36人死亡，49人受伤，社会影响非常恶劣。

根据事故致因理论中的轨迹交叉论，人机系统中存在人的不安全行为和机械或物质危害(物的不安全状态)两类能量逆流序列，当人流与物流发生交叉时，则会发生安全事故，且该交叉点即是事故发生的“时、空”[1]。对于大型活动安全事故来说，安全费用投入不足会造成物的不安全状态，加之人的不安全行为，二者交叉发生在大型活动举办场所内，即发生了安全事故。

为了避免大型活动中发生安全事故，大型活动主办方应投入安全措施费用。然而，安全与经济效益通常被企业管理者视为相互矛盾的两个方面，重视安全就会降低经济效益产出，因此往往忽略了在安全措施上的投入，造成安全事故隐患。本文引入博弈论理论，通过分析大型活动主办方与参与者就安全费用投入展开的博弈，为大型活动主办方提供参考借鉴。

1 安全费用投入博弈分析

为了简化模型以便进行研究，本文将大型活动参与人员看作一个整体，作为博弈方之一；将活动主办方看作是另一个博弈方，建立起博弈模型。

1.1 模型假设

虽然活动主办方在活动筹备阶段已经投入的安全费用，但是考略到在活动主办过程中主办方仍需考略追加投入，因此本研究将安全费用投入博弈简化为完全信息静态博弈。根据博弈论理论[2～3]，此时的博弈各要素如下。

(1)局中人。

局中人是指博弈过程中的博弈参与者。本研究将局中人简化为活动参与者(局中人1)和大型活动主办方(局中人2)。

(2)策略集。

设局中人i的第j个策略为aij，局中人i的策略集为Si，即：

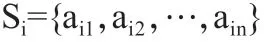
上式表明，局中人i的策略集有n种策略选择。

在安全费用投入博弈模型中，活动参与者(局中人1)的策略集S1中，a11表示安全行为；a12表示不安全行为；活动主办方的策略集S1中，a21表示投入足够安全费用；a22不投入足够安全费用，由于机械设备等。

(3)收益与支付矩阵。

根据两名局中人活动参与者和主办方的策略集，确定安全费用投入博弈中的支付矩阵，如表1所示。

表1 安全费用投入博弈支付矩阵

上述支付矩阵中，a表示主办方投入安全费用产生的成本(支出)；b表示参与者不安全行为收到伤害造成的损失。由于参与者在大型活动中遭受了安全事故，其赔偿势必要由活动主办方承担部分或全部。因此，假设主办方投入足够的安全费用时赔偿为c，未投入足够的安全费用时为d，显然d＞c。

1.2 纳什均衡解

应用求解完全信息静态博弈的划线法，求解过程如下[4]。

(1)当活动主办方选择“投入足够安全费用策略”时，活动参与者选择安全行为策略收益最高，因此在第一象限内的“0”下面划线。

(2)当活动主办方选择“不投入足够安全费用”策略时，活动参与者选择安全行为策略收益最高，因此在第二象限内的第一个“0”下面划线。根据(1)(2)的分析可知，“安全行为”是参与者的严格占优策略。

(3)当活动参与者选择“安全行为”策略时，主办方选择“不投入足够安全费用”策略收益最高，因此在第二象限内的第二个“0”下面划线。

(4)当活动参与者选择“不安全行为”策略时，主办方选择哪种策略要视d和(a+c)的大小关系而定。当d＞a+c时，主办方选择“投入足够安全费用”策略收益最高，因此在-(a+c)下面划线；当d＜a+c时，主办方选择“不投入足够安全费用”策略收益最高，因此在-d下面划线；当d=a+c时，主办方选择策略两种的收益相同，因此可同时在第三象限内的-(a+c)和第四象限内的-d下面划线。注意：不论是上述何种情况发生，第三象限和第四象限内的决策组合均不会出现双划线的情况，因此不影响纳什均衡结果。

由划线法可知，统一决策象限内的双划线组合即为纳什均衡结果。因此，(安全行为，不投入足够安全费用)即为纳什均衡解。

1.3 混合策略均衡解

对于完全信息静态博弈，我们可以求解混合策略均衡解。混合策略纳什均衡解，即假定局中人以一定的概率随机选择某种策略。

在安全费用投入博弈中，假设活动参与者选择“安全行为”策略的概率为p，“不安全行为”策略的概率为1-p，以此保证活动主办方选择“投入足够安全费用”和“不投入足够安全费用”两种策略无差异；另外，活动主办方选择“投入足够安全费用”策略的概率为q，选择“不投入足够安全费用”两种策略的概率为1-q，以此保证参与者选择“安全行为”和“不安全行为”两种策略无差异。注意，这里的p和q还以有其他理解：活动参与者由于安全素质有限，因此有p的几率进行安全行为，有1-p的概率做出不安全行为；主办方受到企业经济效益(或活动预期效益)制约，不能投入足够的安全费用，此时的安全费用投入率为q。显然这种理解方式更符合实际情况。

p，q的求解过程如下：

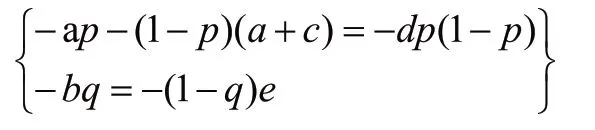
1.4 博弈结果分析

(1)根据纳什均衡解可知，大型活动参与者会选择“安全行为”，而活动主办方会选择“不投入足够安全费用”。显然这个均衡解不符合于安全生产管理所期盼的纳什均衡：(安全行为，投入足够安全费用)。为此，相关方面应该采取措施使现阶段的纳什均衡解转移至期盼解，具体可包括政府加大日常安全检查和处罚力度、构建企业安全文化等[5]。

以政府加大安全检查和惩处力度为例，此时支付矩阵变更为如表2所示(此时f＞a)。

表2 政府加大检查惩处力度时的支付矩阵

根据支付矩阵及划线法求解，此时的纳什均衡为(安全行为，投入足够安全费用)，符合安全生产目标要求。

(2)根据纳什均衡解可知，当(d-c)相对于a无穷大时，p无限趋近于1，即活动参与者选择“安全行为”的概率无限趋近于1，此时符合安全生产管理要求；当e相对于b无穷大时，q无限趋近于1，即活动主办方选择“投入足够安全费用”的概率无限趋近于1，此时符合安全生产管理要求。为此，政府应该加强事故惩处力度和安全检查力度，敦促活动主办方投入足够安全费用。

2 确保安全费用投入的对策措施

通过上文的博弈分析，笔者认为保证大型活动主办方确保安全费用投入，可以从以下几个方面入手。

(1)政府加大安全检查和处罚力度。

政府加大安全检查和惩处力度，有利于及时发现大型活动主办方在安全设备设施、安保人员、活动场所等方面的不足，及时敦促主办方积极投入安全费用，确保设备设施无缺陷、安保力量充足、活动场所安全性高。

(2)政府加大事故惩处力度。

政府加大事故惩处力度，尤其是事故惩处力度应远远大于投入足够安全费用的成本，如此一来活动主办方自然会做出权衡，积极投入安全费用。

(3)企业构建安全文化。

企业方面应该积极构建本单位的安全文化[5]，积极建立和落实安全生产责任制，建立完善的安全生产费用提取制度，确保安全费用的投入。

3 结语

本文引入博弈论的相关理论和方法，通过对大型活动主办方和参与者在安全费用投入方面展开的博弈，分析了大型活动安全费用投入不到位的症结所在。为了积极避免大型活动安全事故，从保证安全费用投入方面考虑，政府应该加大日常安全检查和处罚力度、加大事故惩处力度，企业方面应该积极构建安全文化。