加速器隧道控制网变形可监测性及稳定性分析

郭迎钢，李宗春，刘忠贺，赵文斌，袁建东，王志颖

(1.中国人民解放军战略支援部队信息工程大学，河南 郑州 450001；2.中国科学院 上海应用物理研究所，上海 201800；3.中国科学院 近代物理研究所，甘肃 兰州 730000)

变形监测与分析对于大坝等大型工程建构筑物和边坡、矿区等重点区域有重要的意义[1-3]。粒子加速器是研究高能物理和粒子的大型科学实验装置[4-5]，为保证粒子束尽可能沿设计轨道运行，需对设备元件和测量控制网[6-8]进行精确的测量及变形监测[9-11]。设备元件的变形监测主要采用静力水准[12-14]和位移传感器[15-17]等技术，精度可达μm级。隧道控制网的测量以激光跟踪仪[18-19]为主要工具，通过定期复测(一般每年1次)来维持、更新控制网点的坐标数据，并分析其变形情况。

隧道控制网是加速器元件安装定位和检查调整的直接测量依据，对其复测结果的分析和有效利用具有重要意义。目前，国内对隧道控制网复测结果普遍采用的处理方法是：以最新1期的观测值平差结果直接作为控制基准，结合设备增减情况分析前后2期的点坐标，对坐标变化异常的控制点进行标记并弃用。该处理方法不甚严谨：1) 坐标变化异常阈值凭经验选取，缺乏理论依据；2) 有可能弃用稳定点，造成控制网信息的浪费；3) 有可能将极个别变形点纳入控制网，影响对应区域的器件安装精度，从而降低加速器的工作效率；4) 若有未能发现的控制网整体变形，有可能导致元器件的大规模错误调整，导致本可正常运行的加速器作不必要的调整。该方法实质上是未引入控制网稳定性检验的理论和方法。为此，本文将三维控制网变形可监测性和稳定性分析理论应用于粒子加速器隧道控制网，以期更好地指导实践。

1 三维控制网变形的可监测性

控制网的变形可监测性，也即控制网的灵敏度问题。通过分析控制网可能监测到的最小变形值及其方向，能得出控制网监测变形的能力。可将控制网的变形视为模型误差[20]，按照附加系统参数模型进行求解，利用线性假设法进行显著性检验，并以灵敏度椭球的形式来直观表示三维控制网可测定变形的下界值。

1.1 变形模型和假设检验

设三维控制网2期观测的误差方程为：

V1=A1X1-l1

V2=A2X2-l2

(1)

式中：A1和A2分别为2期观测的系数矩阵；X1和X2为未知参数；l1和l2为自由项；V1和V2为观测值改正数。

(2)

当H0∶d=0成立时，可导出F分布的检验统计量：

(3)

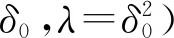
1.2 灵敏度椭球

根据二维控制网中灵敏度椭圆元素的表达式[21]，对三维控制网的灵敏度椭球元素的计算公式进行推导。在三维控制网中，1个控制点的三维坐标变形向量可表示为：

d=|d|e

(4)

由式(4)可得：

(5)

(6)

λ1～λ3及其对应的方向余弦(li,mi,ni)即为灵敏度椭球元素。灵敏度椭球的边界是可测定变形的下界值，即在灵敏度椭球的边界内，按照给定的显著水平和检验功效，在现有的测量精度、控制网网形等条件下，无法判断该点是否发生了变形。

2 隧道控制网的稳定性

控制点的稳定与否的判断是隧道控制网复测成果分析的重要内容。控制网的稳定性分析方法有比较法、t检验法、平均间隙法[22]等。比较法和t检验法适用于图形简单、点数较少的监测网，而加速器隧道控制网图形结构复杂、控制点数量众多，为此本文优选平均间隙法来寻找变形点。稳定性分析中涉及到参考基准的选择，由于控制网中所有控制点几乎都在同一精度等级，因此选取重心基准进行平差。

2.1 整体稳定性检验

设隧道控制网的2期观测取重心基准平差后，网点的坐标差向量及其权阵为：

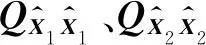
2.2 平均间隙法逐点检验

(7)

对控制网中的每个点计算对应的ωi和ΔRi。首先剔除第j点ωj=max{ωi}，然后通过式(8)检验：

(8)

若不通过，重复上述过程；否则结束逐点检验，剩下的控制点是稳定的。

3 实验分析

根据加速器形状的不同，控制网主要分为直线形和环形两种。控制点一般间隔一定距离分布在地面、墙面和隧道顶部便于观测的位置，采用激光跟踪仪自由设站法进行观测，如图1所示。

3.1 变形可监测性分析

控制点的分布、跟踪仪设站位置和测量方案等因素影响着控制网的网形，进而影响控制网的变形可监测性。假设某直线形加速器控制网的设计情况为：总长100 m，沿隧道纵向每6 m分布1组控制点，每组控制点有5个，隧道顶部布置1个、底部布置2个、两侧壁面各布置1个；跟踪仪测量时，在每2组控制点所在截面的中间隧道中轴线上架设1站，仪器中心高1.4 m；每1站上对邻近的4个截面上的20个点进行观测。假设某环形加速器的直径为100 m，控制点分布、仪器架设位置和观测方案与直线形控制网相似。以下对这2种三维控制网的变形可监测性进行分析。

根据直线形加速器和环形加速器控制网的观测方案得到的控制网网形示于图2。

取显著水平α=0.001、检验功效β=0.80时，δ0=4.13；取先验单位权中误差σ0=0.02 mm，按照式(6)计算每个控制点的灵敏度椭球，结果示于图3。

对于直线形控制网，由图3a可知，两端控制点上灵敏度椭球的体积明显大于中间控制点的，表明中间控制点上的变形更易被监测到；中间控制点上的灵敏度椭球体积相差不大，各点监测能力相近。对于环形控制网，观察图3b可知，由于整个控制网首尾相连，所有控制点上的灵敏度椭球体积相近，监测变形的能力较为一致。从局部放大图可看出，直线形控制网灵敏度椭球的长轴方向近似分布在竖向上，最弱监测变形的方向为竖向，与精度最弱方向基本一致；环形控制网各点灵敏度椭球的主轴方向不一致，表示不同方向上的变形可监测能力不同，但长轴方向与竖向夹角较小，表明竖向的灵敏度较低。分析竖向上灵敏度较低的原因如下：由于控制点由多个测站进行交会观测，这些测站在水平方向分布较为均匀，交会质量较好；竖向上测站的高度单一，交会质量较差。

图1 隧道内控制点分布Fig.1 Control point distribution in tunnel

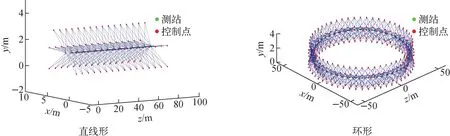
图2 控制网网形Fig.2 Configuration of control network

图3 灵敏度椭球分布Fig.3 Distribution of sensitivity ellipsoid

图4 灵敏度椭球主轴长度Fig.4 Axis length of sensitivity ellipsoid

直线形控制网从某一端开始编号，起始截面内的5个控制点依次命名为1～5号点，环形控制网由于首尾相接，不存在端点，故任意选取某个截面进行编号。根据式(6)计算出2个控制网所有控制点的灵敏度椭球3个主轴的长度|d|max、|d|med、|d|min，将椭球的3个主轴由长到短依次命名为第1主轴、第2主轴和第3主轴，如图4所示，部分控制点的灵敏度椭球参数列于表1，其中1、2号点为端点，其余为中间点。

图4纵坐标的最大值和最小值能反映出控制网的整体灵敏度指标，直线形控制网的|d|max=0.249 mm，|d|min=0.030 mm；环形控制网的|d|max=0.142 mm，|d|min=0.027 mm。由表1可看出，直线形控制网端点(以1、2号点为例)灵敏度椭球的第1主轴长度(|d|max)与中间控制点灵敏度椭球的第1主轴长度相比明显较大；环形控制网灵敏度椭球的第1主轴长度相近。对于中间的大部分控制点(以8、12、22、50号点为例)，其灵敏度椭球的第2主轴(|d|med)和第3主轴(|d|min)的长度相差较小。

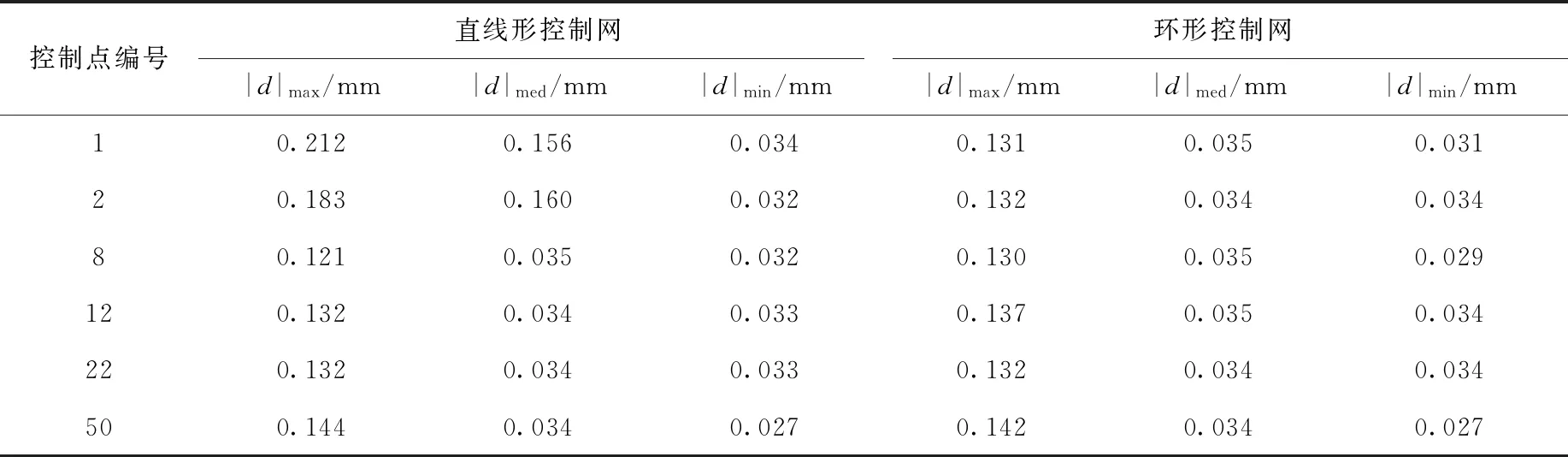
表1 灵敏度椭球元素参数Table 1 Parameter of sensitivity ellipsoid

3.2 稳定性分析

上海光源(SSRF)储存环控制网每年都要进行1次以上的复测。本文以2016、2017年的复测数据为例，对其进行稳定性分析。

SSRF储存环控制网有多类控制点，其命名规则为：BD表示外墙点；BT表示支柱点；BM表示地面点；BQ表示锯齿墙点。计算储存环上268个控制点2期观测的坐标差值，坐标差矢量的三维分布如图5a所示。以环中心与控制点BD808的连线为y轴、控制点与环中心连线与y轴的夹角为θ，逆时针方向为正。以BD808为原点将环形展开，得到的三维坐标差随θ增大的分布情况如图5b所示。

由图5a可知，2期数据在竖直方向上的坐标差大于水平方向上的坐标差，径向上的坐标差大于沿隧道前进方向上的坐标差。面向BD101控制点观察整个环形的坐标差分布，呈现出前后下沉、左右上升的变形现象。在局部区域上，控制点的坐标分量变化规律近似一致，表明相邻点具有相同的变形趋势。由图5b可知，2期数据的坐标差大部分在0.3～0.9 mm范围内。

为分析控制网整体是否发生了变形及控制网中哪些点发生了变形，按照式(8)构造检验统计量。取显著水平α=0.001，用2017年的控制网观测成果计算得：

15.60>F(α,m,n-t-m)=0.82

由此可知，控制网整体稳定性检验未通过，说明控制网中某些点发生了位移。

按照平均间隙法进行逐点检验，ωi的最大值为0.49 mm2，对应的70号点BD417为不稳定点，将其剔除；对剩下的点进行检验，ωi的最大值为0.48 mm2，对应的154号点BD821为不稳定点，…，重复以上步骤，在剔除124个不稳定点后，图形一致性检验合格，此时ωi的最大值为0.05 mm2，表明剩下的144个点是稳定点。其中具有代表性的点的坐标差与变形量列于表2。

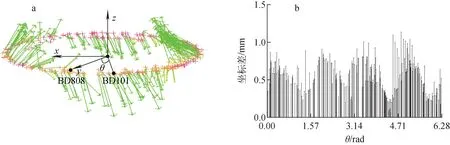
图5 2期观测的坐标差Fig.5 Coordinate difference of two terms observations

表2 部分点的变形量Table 2 Deformation of some typical control points

在图5的基础上，将124个变形点的变形量用绿色针状图显示，如图6所示。

图6 控制网点的变形量Fig.6 Deformation of control point

图6中，红色椭圆标注的部分控制点(如BD304、BD306、BT313等)，虽然2期坐标的坐标差较大，但由平均间隙法可知这些点为稳定点；蓝色椭圆中标注的控制点(如BD207、BD208、BD210等)，虽然2期坐标的坐标差较小，但由平均间隙法可知这些点为变形点。因此，在利用加速器控制网的多期测量数据分析控制网点的变形情况时，不能简单地根据2期坐标差来分析控制网变形情况，应严格采用平均间隙法进行分析，通过选用稳定点和变形较小的点来指导加速器元器件的安装更加可靠。

表2中BD603点和BM111点的变形量分别为该控制网能发现的最小和最大变形量，最小变形量为0.17 mm(BD603点)，反映出该控制网的变形可监测性较强；最大变形量为1.13 mm(BM111点)，表明该控制网的变形量在1.2 mm以内。将图6中变形点的情况进行统计，结果列于表3。

表3 各类变形点的统计情况Table 3 Statistical result of different kinds of points

由表3中统计的变形点所占比例来看，BM点

4 结论

本文研究了粒子加速器三维控制网的变形可监测性和稳定性分析方法。在二维控制网变形可监测性理论基础上，推导了三维控制网灵敏度椭球元素的计算公式，并结合三维控制网的变形模型和稳定性分析理论，通过仿真设计对直线形和环形两种典型的加速器控制网进行了变形可监测性分析，以SSRF储存环控制网2016、2017年的复测数据为例进行了稳定性分析，得出如下观点。

1) 直线形控制网两端控制点的变形可监测性明显弱于中间控制点的变形可监测性，环形控制网的变形可监测性较为均匀；网形对灵敏性椭球有较明显的影响，加速器控制网点的在垂直方向上的灵敏性较弱。

2) SSRF隧道控制网2016、2017年2期控制点坐标在竖直方向上的坐标差大于水平方向上的坐标差，径向上的坐标差大于沿隧道前进方向上的坐标差；整体呈现出前后下沉、左右上升的变形现象。

3) 采用平均间隙法进行变形分析时，2期数据中坐标差大的点未必是变形点，坐标差较小的点有可能是变形点，坐标差并不能严格反映出控制网的变形情况。

4) SSRF隧道控制网监测变形的能力较强，最小可监测出0.17 mm的变形量；变形点的变形量不大，均在1.2 mm以内。根据变形量的平均值，4类控制点的稳定性从强到弱依次为地面点、外墙点、锯齿墙点和支柱点，地面点的稳定性最优。在加速器元器件安装调整时，应根据稳定性分析结果选择稳定性好的点作为基准。