灰色多属性风险决策方法及其应用研究

张金波 施明华 李晓然

（皖西学院 金融与数学学院，安徽 六安 237012）

0 引言

当前，我国正处在社会转型和经济转轨的阶段，决策者所面临的决策信息常带有较大的不确定性，决策风险也随之增大。如果能确定发生状况的客观概率或者主观概率，则称这样的决策为风险决策。风险决策广泛存在于经济、政治、贸易活动中，并得到越来越多研究者关注。一方面，随着我国经济社会的发展，决策者很难通过单个属性对候选对象进行合理评价，往往需要借助多个属性指标，这便形成了多属性决策问题[1-3]。例如Li MY等[4-7]讨论了多属性风险决策问题，Zhou H等[8-10]考虑了灰色多属性风险决策问题,但很少有涉及灰色区间数的多属性风险决策问题的研究报道。Li Z等[11]将决策者的风险偏好划分为三种不同的类型，然后建立相应的区间灰数多属性决策方法，并通过一个实际的投票实例说明了该方法的实用性和有效性。刘光凤等[12]定义了灰色隶属度，解决了概率为区间数的灰色多属性风险决策问题。孙丽萍等[13]利用证据理论得到灰色信息置信矩阵，构建风险评价模型，并用于度量原油舱的风险。徐选华等[14]基于后悔理论获取决策信息为区间数的决策对象感知效用，在此基础上，给出各个决策对象的风险熵，进而给出一种应急方案的排序。

另一方面，区间数的比较在决策过程中起着至关重要的作用，因为决策问题大都最终演变为区间数的比较与排序问题。虽然区间排序的文章发表较多，但至今没有出现一种被广泛认可的方法。大多数文献采用均是徐泽水[15]所定义的区间数排序方法，Li Z等[11-14]也不例外。也有一些学者尝试对该方法进行改进，例如Sevastianov等[16]依据区间坐标值给出一种简洁易算的排序方式，但信息损失较大，排序不稳定。张吉军[17]提高了精度，但给出的计算公式复杂，不便实际应用。因此本文尝试提出一种新的灰色随机变量排序方式，并应用于灰色多属性风险决策问题。

1 灰色随机变量及其排序

对于只知道其变化范围,无法给出精确值的数称之为灰数，灰数是灰色系统理论的基本“单元”或“细胞”，通常记为“⊗”[18]。

定义1[18]取值连续充满某个区间，并且该区间具有上界和下界，则称这样的灰数为连续型区间灰数，记为⊗∈[a，b]。 假定⊗1∈[a，b]，⊗2∈[c，d]为2个连续型区间灰数，k为正常数，则有：

（1）⊗1±⊗2∈[a±c，b±d]；

（2）k⊗1∈[ka，kb]；

（3）-⊗1∈[-b，-a]。

定义2 若随机变量的取值为有限个不同的连续型区间灰数⊗，则称之为连续型灰色随机变量，记为ξ（⊗）。其分布函数如表1所示：

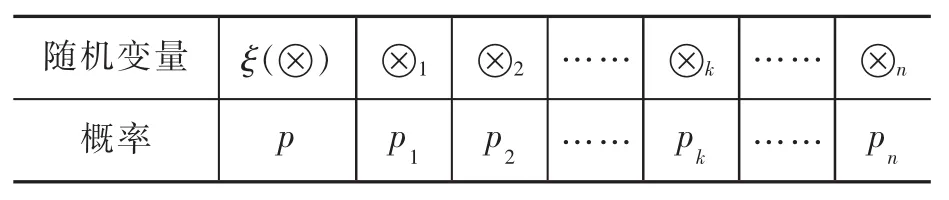
表1 ξ（⊗）的分布函数

定义3[9]设⊗1∈[a，b]，⊗2∈[c，d]，且设 l1=b-a，l2=d-c，则⊗1大于⊗2的可能度定义如下：

目前文献中给出的区间优势判别方法，基本都是定义3及其等价形式。但这种可能度对区间数排序会导致有效信息的丢失。例如，情况1：⊗1∈[2，2.5]与⊗2∈[1，3]；情况 2：⊗3∈[2.1，2.5]与⊗4∈[1，3.1]，通过定义3 得出 p（⊗2≥⊗1）=p（⊗4≥⊗3）=0.4。事实上情况1中⊗2比⊗1的绝对优势范围为[2.5，3]小于⊗3比⊗2的绝对优势范围[2.5，3.1]，同时⊗2落在[2.5，3]的可能度0.5/3也小于⊗4落在[2.5，3.1]的可能度0.6/3.1。两种情况对比缩小的是均衡优势区间，范围从[2，2.5]变至[2.1，2.5]。因此不应该出现 p（⊗1≥⊗2）=p（⊗3≥⊗4）。 为对上述排序方式加以改进，本文提出一种新的区间数排序方法。

定义4 设⊗1∈[a，b]，⊗2∈[c，d]，且设 l1=ba，l2=d-c，则⊗2大于⊗1的可能度定义如下：

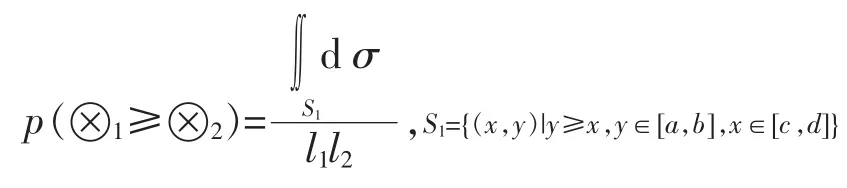
定理1 设⊗1∈[a，b]，⊗2∈[c，d]，∈[e，f]则

1-1 0≤p（⊗1≥⊗2）≤1；

1-2 p（⊗1≥⊗2）+p（⊗2＞⊗1）=1，特别的

p（⊗1≥⊗1）=1/2；

1-3 p（⊗1≥⊗2）=p（⊗1≤⊗2）；

1-4 如果 p（⊗1≥⊗2）≥1/2，p（⊗2≥⊗3）≥1/2，则 p（⊗1≥⊗3）≥1/2。

证明：根据定义4 显然可得（1）、（2）、（3），下面证明（4）。由定义4 知 p（⊗1≥⊗3）=p（⊗1≥⊗2）·p（⊗2≥⊗3）+p（⊗2≥⊗1）p（⊗1≥⊗3）+p（⊗1≥⊗3）·p（⊗3≥⊗2），

移项得

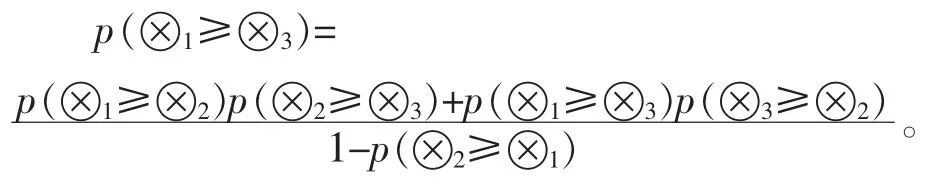
由（1）、（2）可知

据此可得 p（⊗1≥⊗3）≥1/2。

定义5 ⊗1∈[a，b]，⊗2∈[c，d]，若 p（⊗1≥⊗2）≥1/2 则认为存在序关系⊗1≻⊗2；若 p（⊗2≥⊗1）≥1/2 则认为存在序关系⊗2≻⊗1；若 p（⊗2≥⊗1）=1/2则认为存在序关系⊗2=⊗1。

由定理1可知，定义5给出的序是一种严格偏序。对于情况 1：⊗1∈[2，2.5]与⊗2∈[1，3]；情况2：⊗3∈[2.1，2.5]与⊗4∈[1，3.1]，通过定义5 得出p（⊗2≥⊗1）=0.375，p（⊗4≥⊗3）=0.4。可见定义5较好的保留了信息。在定义5的基础上，我们结合期望理论，给出如下判断连续型灰色随机变量的方法。

定义6 ξ（⊗1）与 ξ（⊗2）为 2 个连续型灰色随机变量，其分布函数如表2和表3所示，则ξ（⊗1）大于 ξ（⊗2）的可能度定义如下：

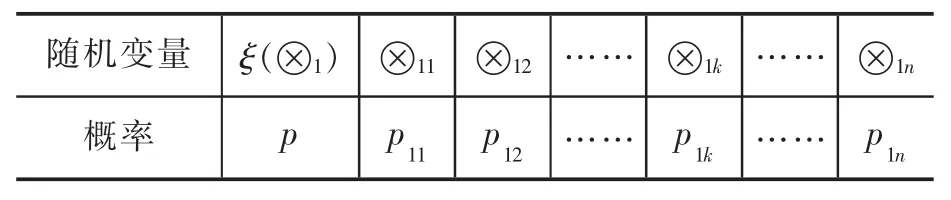
表2 ξ（⊗1）的分布函数

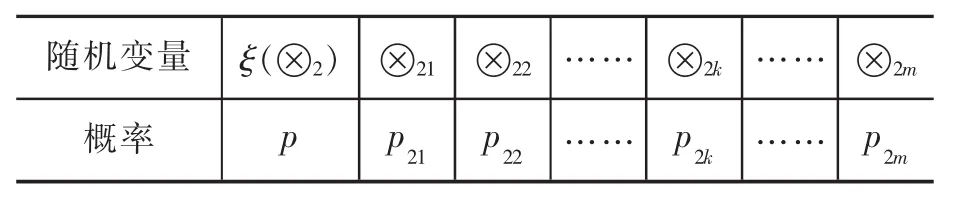
表3 ξ（⊗2）的分布函数

定理2 ξ（⊗1）、ξ（⊗2）、ξ（⊗3）为连续型灰色随机变量，则

2-1 0≤p（ξ（⊗1）≥ξ（⊗2））≤1；

2-2 p（ξ（⊗1）≥ξ（⊗2））+p（ξ（⊗2）＞ξ（⊗1））=1，特别的 p（ξ（⊗1）≥ξ（⊗1））=1/2；

2-3 p（ξ（⊗1）≥ξ（⊗2））=p（ξ（⊗1）≤ξ（⊗1））；

2-4 如果 p（ξ（⊗1）≥ξ（⊗2））≥1/2，p（⊗2≤⊗3）≥1/2，则 p（⊗1≥⊗3）≥1/2。

证明：记 p（⊗1i≥⊗2j），i，j∈{1，2，…，n}最大值和最小值分别为M与m，由定理1（1）可知m≥0，M≤1，可得

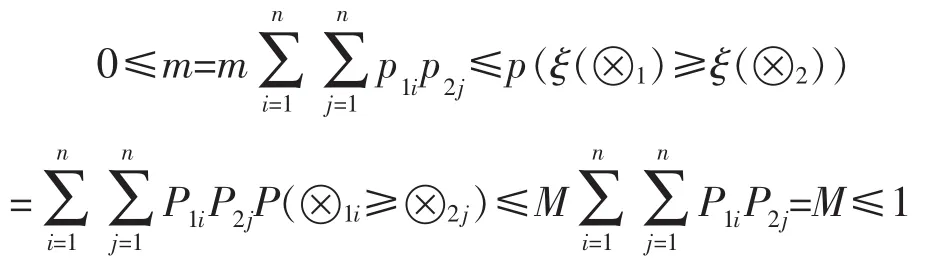
因此定理2-1成立，下面证明定理2-2。

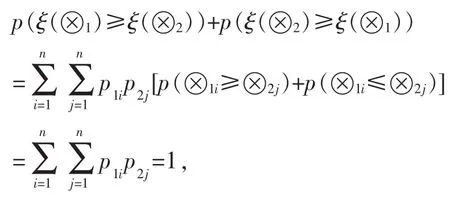
令 ξ（⊗2）=ξ（⊗1）带入上式，显然有 p（ξ（⊗1）≥ξ（⊗1））=1/2。 故定理2-2 得证。

利用定理1-3，显然定理2-3成立。因此下面只需证明定理2-4即可。

因此

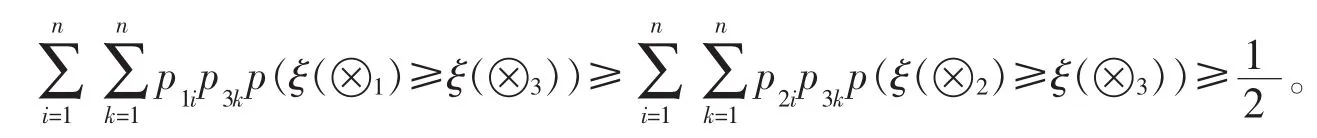
定义7 ξ（⊗1）与（ξ（⊗2）为 2 个连续型灰色随机变量，若 p（ξ（⊗1）≥ξ（⊗2））≥1/2 则认为存在序关系 ξ（⊗1）≻ξ（⊗2）；若 p（ξ（⊗2）≥ξ（⊗1））≥1/2则认为存在序关系 ξ（⊗2）≻ξ（⊗1）；若 p（ξ（⊗1）≥ξ（⊗2））≥1/2 则认为存在序关系 ξ（⊗1）=ξ（⊗2）。

2 灰色风险决策算法

对于一个灰色风险多指标决策问题，这里我们假定其概率是确定的，权重是未知的，并且对各方案没有偏好。 设指标集 G={g1，…，gk，…gn}，方案集 X={x1，…，xk，…xm}，指标 gk∈G 具有种状态，并且在每种状态下具有的概率为，指标集的权重为{w1，…wk，…wn}。 方案xk，k∈{1，2，…，m}在指标 g1，l∈{1，2，…，n}下取值均为连续型区间数。则 X={x1，…xk，…xm}每个元素均为连续型灰色随机变量。如表4所示。

表4 指标gk的风险决策表

下面给出一种基于连续型灰色随机变量排序准则的风险决策方法，步骤如下：

步骤1：利用定义7构造方案集X={x1，…xk，…xm}在指标 g1，l∈{1，2，…，n}下的判断矩阵为，其中。

步骤2：构造加权综合矩阵B＝[bj]mxm，其中。由定理2可得该矩阵是互补判断矩阵。计算B＝[bj]mxm的排序向量

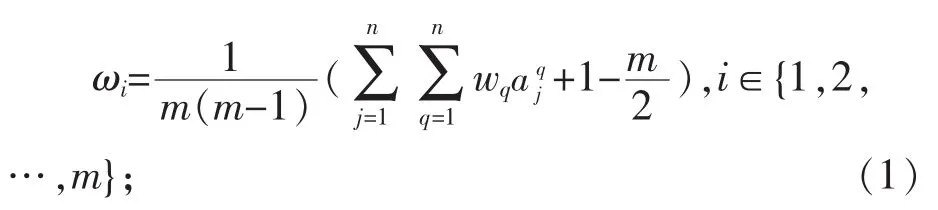
步骤4：计算 ωi的满意度指标，建立优化模型。假定求得最优解为，带入（1）式由 ωi大小对方案进行排序。

3 实例分析

能源问题一直困扰人类，越来越多的国家和地区致力于开发和利用新能源技术。目前，煤层气、油砂、页岩油、燃料乙醇和生物柴油在一些地方得到了有效的发展。Nea Kessani是希腊北部的一个农村社区，该地区的经济衰退需要在清洁能源和先进制造业中创造新的就业岗位，实现传统农业向现代工业的转变。当地企业计划投资开发低焓地热资源，市场预测能源开采有四种可能状况，分别为很好 s1、好 s2、一般 s3和差 s4，现设计四种方案，考虑三个指标，分别为直接收益u1，间接收益u2和污染损失u3。各种指标的风险决策表如表 5～7所示，求最优方案[7]。

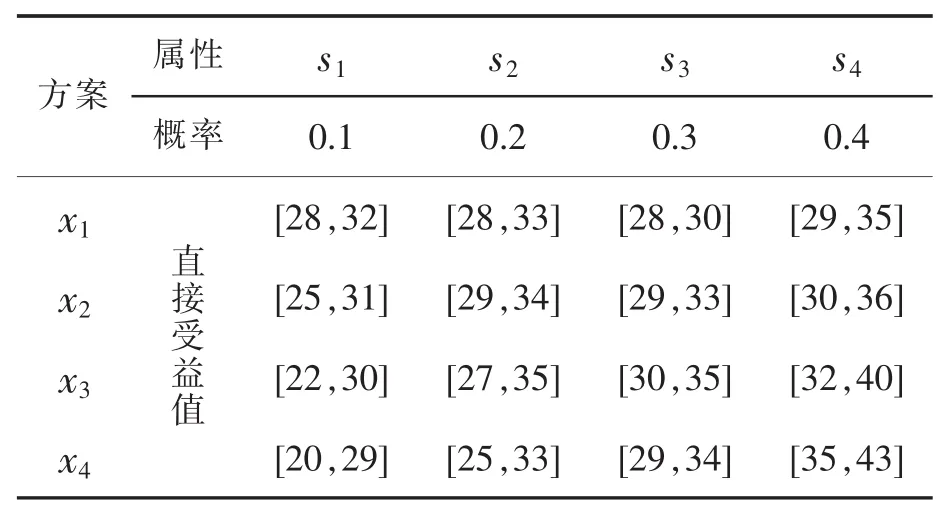
表5 直接收益决策表[7]

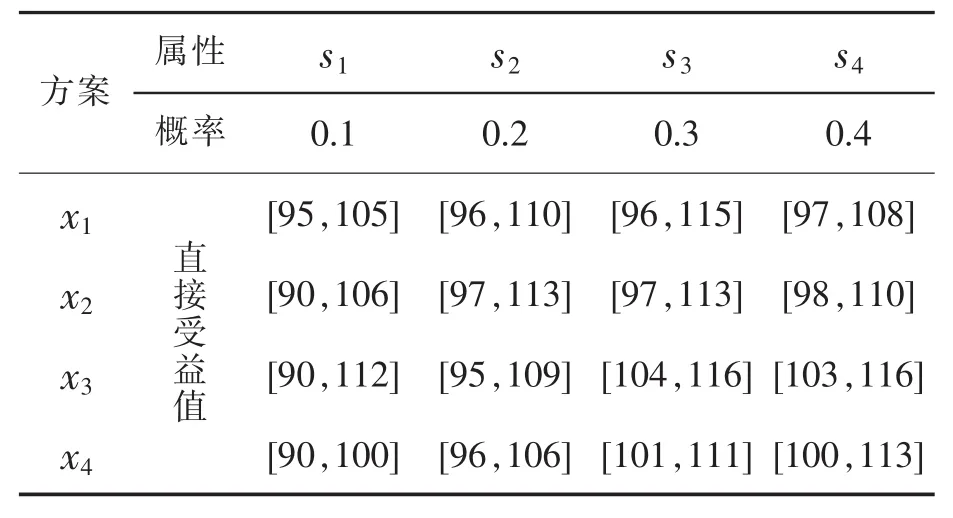
表6 间接收益决策表[7]

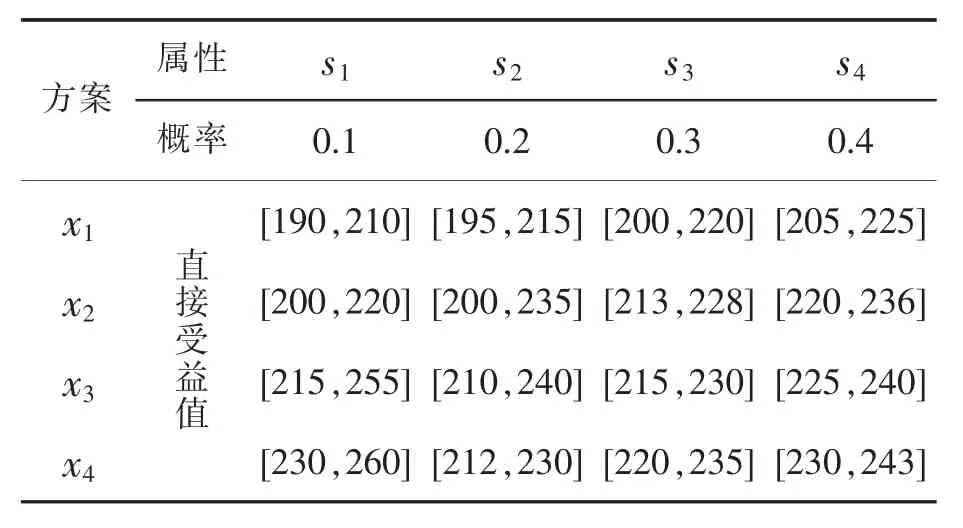
表7 污染损失决策表[7]

步骤1 首先将指标一致化，利用定义7计算得出三个指标的判断矩阵如下：

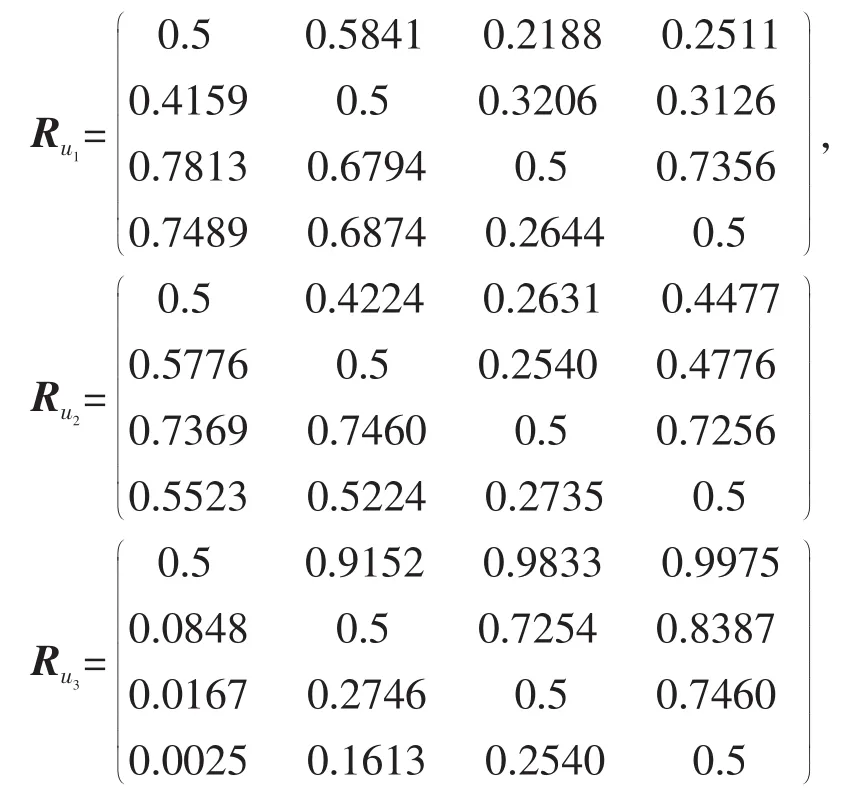
步骤2 记u1，u2与u3的权重分别记为w1，w2与w3，则由公式（1）计算可得各方案的排序指标

步骤3 参考熵权法和主观权重法计算的权重值，给出权重指标的取值范围

由优化模型 max ωi，s.t.w∈Ω，求得 ωi的最大理想值为：，求得最小理想值为：；

步骤4 求解优化模型

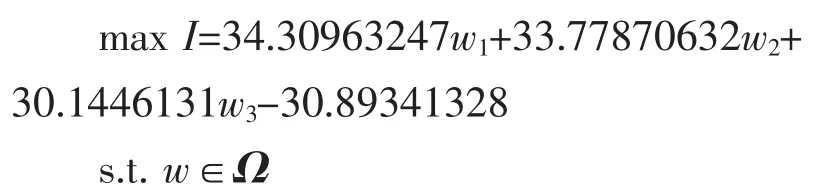
解得 w1=0.65，w2=0.2 与 w3=0.15，带入（1）得ω1=0.237177506，ω2=0.224259089，ω3=0.293750781，ω4=0.244811291。 因此，四种方案的排序为 c2＜c1＜c4＜c3，方案 3 是最佳方案。

若采用陈雯等[7]提出的决策方法求解，可得各方案的相对贴进度 ωi（i=1，2，3，4）分别为

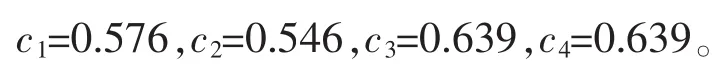
因而，四种方案的排序为 c2＜c1＜c4～c3，即认为方案3和方案4都是最佳方案。明显文献[7]给出的优选指标区分度不高，这主要由于文献[7]的决策模型采用排序方法为定义3，正如前文所述，这种排序可能会导致决策信息的丢失，从而影响决策结果的准确性，而本文的基于期望理论构建的排序方法则能可有效避免这一缺陷，构建的排序方法因而更具科学性。

4 结论

为了更加准确的刻画区间数的大小，本文定义了一种具有严格偏序关系的相对优势度，比王浩伦等[9]研究中的方法更为精细。结合期望效用理论，将该方法用于刻画连续型灰色随机变量的可能度计算。在此基础上提出了灰色风险多指标决策方法，实例分析表明该方法是可行和有效的。此外本文提出的方法计算方便可操作性强，有助于解决供应链管理，风投项目选择等问题，具有一定的应用价值。