不同受力模式下沥青混合料动态模量应变依赖特性研究

周 维 锋

(山西省交通科学研究院，山西 太原 030006)

0 引 言

在沥青路面力学分析中，沥青混凝土的模量是路面力学计算的关键参数之一，其取值直接影响路面结构受力分析结果[1]。对于线粘弹性力学分析体系，通常采用动态模量表征材料粘弹性质。大量的研究表明，沥青混合料的动态模量具有明显的环境和荷载依赖性，其中温度和频率是影响沥青混合料动态模量的两个主要外部因素[2-3]。由于沥青混合料组成物质的多样性和复杂性，导致沥青路面结构的力学响应更接近非线粘弹性体系，即沥青混合料的动态模量与材料的应力状态有关[4]，且不同应力路径、不同试验条件下的材料动态模量值差异较大。

材料的动态模量不仅可以描述材料的粘弹性质，也可以用来描述材料的非线粘弹和损伤性质。但是动态模量作为表征材料力学性质的重要参数，在不同的荷载模式和作用时间下其数值明显不同，进而影响路面材料的力学响应行为和损伤模式。通常，沥青混合料在压缩或剪切荷载条件下，其响应模量主要表现为硬化特征，即随着荷载水平的增加，模量数值逐渐增大；在弯曲或拉伸荷载条件下，沥青混合料表现为软化特征，即模量随着荷载水平的增加而逐渐减小[5]。

综上所述，沥青混合料的动态模量不仅受温度、荷载频率、应变水平的影响[6]，更重要的是受荷载模式的影响，荷载模式直接决定路面材料的损伤和破坏模式。为了能够更为合理地描述沥青混合料非线性应变依赖特性，笔者开展不同受力模式下沥青混合料动态模量试验，为沥青混合料动态模量的应变依赖特性研究提供基础。

笔者通过对沥青混合料进行弯拉和压剪两种受力模式下的频率扫描试验，基于时间-温度等效原理得到沥青混合料在不同应变水平下的Boltzmann动态模量主曲线，并在此基础上通过推导和数值拟合建立了两种沥青混合料在弯拉和压剪受力状态下的动态模量应变依赖模型，为沥青混合料的非线性特征提供合理性描述，为沥青混凝土路面结构设计提供可靠的模量依据。

1 试验材料与方法

1.1 试验材料

频率扫描试验所用材料为某高速公路建设所用沥青混合料。沥青混合料的合成级配为骨架孔隙结构，其参照SAC矿料设计方法，以最大公称粒径4.75、0.075 mm为关键筛孔进行了配合比设计。沥青混合料的油石比以最紧密状态的改进型体积设计为基础，以性能均衡设计为核心，最终确定得到了不同沥青混合料的合理沥青用量。沥青混合料具体信息如表1。

表1 沥青混合料信息Table 1 Information of asphalt mixture

1.2 试件成型与试验设备

采用法国VECTRA公司生产的M2F梯形梁试验设备进行弯拉受力模式下的频率扫描试验。该设备通过偏心转子在梯形梁试件顶部施加水平荷载。试验采用应变控制模式，通过改变偏心转子的偏心度控制荷载的应变水平与加载频率。试验所需试件为梯形梁试件，尺寸为：上底25 mm，下底56 mm，高250 mm，厚25 mm[7]。

采用SHRP的SPT试验仪进行压剪受力模式下的频率扫描试验[8]。采用该设备测量沥青混合料在不同温度、不同频率、不同应变水平下的动态模量。试件成型采用旋转压实成型法，然后从旋转压实成型的φ150×170 mm圆柱体试件中钻芯取出φ100×150 mm芯样进行试验[9]。

1.3 试验方法

频率扫描作为材料流变特性分析的一种手段，要求材料在试验过程中应一直处于线粘弹性区域(liner viscoelastic region, LVR)。因此在频率扫描试验前需要对沥青混合料试件进行应变扫描，以确定材料的线粘弹性区域。相关研究表明，若沥青混合料的动态模量降低至不超过其最大动态模量的10%，则沥青混合料仍然处于线粘弹性区域[10]。在进行频率扫描前对沥青混合料试件进行应变扫描试验，确定沥青混合料在不同试验方法下的LVR。根据应变扫描试验得到的应变扫描结果确定的频率扫描试验方案如下：

1.3.1 弯拉受力模式下的沥青混合料频率扫描试验方案

试验温度为0～40 ℃，共5个温度水平，温度水平依次升高，每个温度水平间隔10 ℃。每个温度试验开始前试件需要在试验温度下保温4 h。每一档温度下，在0.03%～0.09%应变范围内，以0.03%为间隔共设置3个应变水平。扫描频率按照10～40 Hz的连续正弦波进行加载，共8级频率，相邻荷载频率间隔5 Hz。

1.3.2 压剪模式下的沥青混合料频率扫描试验方案

试验温度为0～40 ℃，共5个温度水平，温度水平依次升高，每个温度水平间隔10 ℃。每个温度试验开始前试件需要在试验温度下保温4 h。每一档温度下，在0.03%～0.09%应变范围内，以0.03%为间隔共设置3个应变水平。扫描频率分别为0.01、0.1、0.5、1、5、10、25 Hz。

2 动态模量应变依赖模型确定方法

2.1 动态模量应变依赖模型推导过程

时间-温度等效原理认为，粘弹性材料在不同时间尺度上的力学行为可以通过温度的改变来实现，其本质在于材料粘弹性松弛时间T的温度相关性。即材料的自由体积分数与温度的改变呈线性关系[11]：

f=f0+αT(T-T0)

(1)

式中:f为材料在温度T下的自由体积分数；f0为材料在参考温度T0下的自由体积分数；αT为自由体积分数的热膨胀系数。基于时温等效原理的分析，国内外研究者多采用Boltzmann函数描述沥青混合料复数模量的主曲线，如式(2)：

(2)

式中：y为模量对数值；x为频率值；A1、A2、x0、d为回归系数，其中x0为曲线拐点。y=A1、y=A2为函数的两条渐近线。按照式(2)，可根据沥青混合料的服役温度水平计算动态模量值。为了更加全面地描述温度、频率以及应变对沥青混合料动态模量的变化规律，笔者在Boltzmann函数的基础上构造复数模量主曲面表达式。由此构造基于应变依赖性的沥青混合料主曲面模型，令：A1=a·eb·ε，A2=a·ec·ε，将A1、A2代入式(2)，可得到沥青混合料应变依赖模型，如式(3)：

(3)

式中：T为温度；ε为应变水平；a、b、c、x0、d为回归系数。

2.2 动态模量应变依赖模型确定

根据非线性最小二乘法拟合得到沥青混合料中不同应变水平下的平移后温度-复数模量试验数据，整理成自变量为温度和应变水平，因变量为复数模量对数的数据格式，采用式(3)对其进行回归分析，可得到基于温度参数的沥青混合料复数模量应变依赖模型。该模型采用温度及双参数，通过函数关系表征了沥青混合料的复数模量，使得模量取值变为函数形式，有效避免了路面结构计算分析中沥青混合料模量取为定值所造成的结构计算分析不合理的问题。

3 试验数据处理与拟合

3.1 主曲线拟合

按照2.1节所述主曲线拟合法，采用Boltzmann主曲线模型，如式(2)，通过非线性拟合得到沥青混合料在不同受力模式、不同应变水平下以10 Hz为基准频率的动态模量主曲线。拟合得到的主曲线参数如表2。

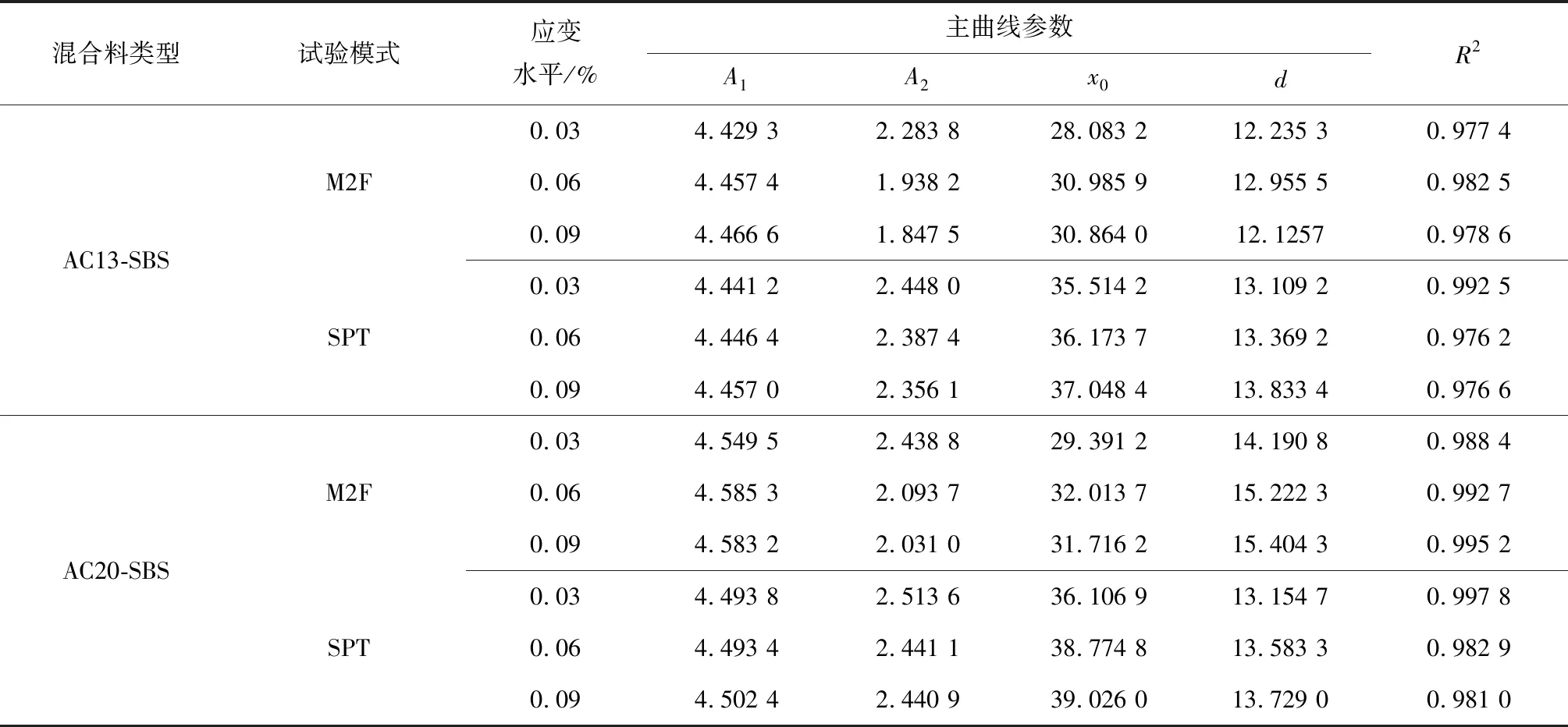
表2 主曲线参数Table 2 Fitting parameter of master curve

由表2可知，对于两种沥青混合料，不论是在弯拉还是压剪模式下，采用Boltzmann主曲线模型对沥青混合料动态模量主曲线进行拟合，拟合精度均较高。

根据拟合得到的主曲线参数，以温度为横坐标、动态模量的对数值即复数模量(lgE)为纵坐标绘制得到沥青混合料动态模量主曲线，如图1、图2。

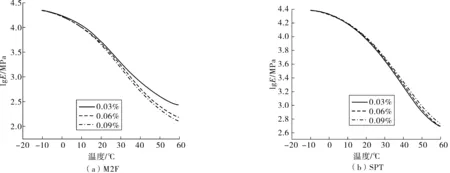
图1 AC13-SBS复数模量主曲线Fig. 1 Complex modulus master curve of AC13-SBS

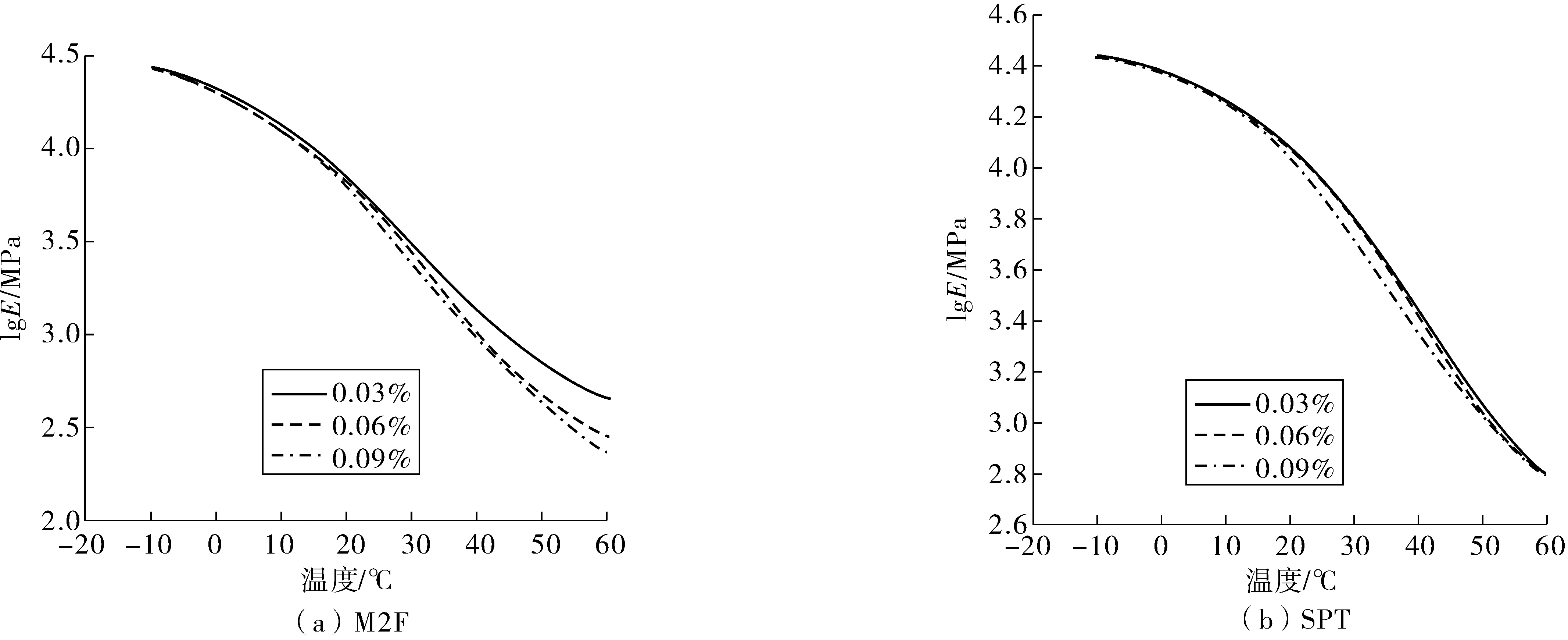
图2 AC20-SBS复数模量主曲线Fig. 2 Complex modulus master curve of AC20-SBS

分析图1、图2中沥青混合料的动态模量主曲线可以发现，沥青混合料不同应变水平下的动态模量值在低温区并无明显差距。随着温度的升高，当材料进入常温区和高温区后，应变对沥青混合料的影响逐渐明显，其动态模量主曲线出现了较大差异，即在低温条件下材料的应变依赖性并不明显。而随着温度的升高，材料的应变依赖性逐渐增强，即材料的非线性逐渐增强。

比较材料在不同受力模式下的动态模量主曲线变化趋势可得：在弯拉受力模式下，材料的动态模量值随着应变水平的升高而降低，而在压剪模式下材料的动态模量值随着应变水平的升高而增大，即材料在弯拉模式下表现出“软化特性”，而在压剪模式下表现出“硬化特性”。这也反应了不同受力模式下材料的应变依赖特性不同。另外，由图1、图2可以发现，对于沥青混合料，在弯拉受力模式下，应变水平对材料的动态模量影响较大，而在压剪受力模式下，应变水平对材料的动态模量影响较小。

3.2 应变依赖模型

根据2.2节所述应变依赖模型确定方法，采用沥青混合料应变依赖模型，如式(3)，对试验数据进行非线性拟合，得到两种沥青混合料的应变依赖模型。拟合得到的沥青混合料不同受力模式下的应变依赖模型参数如表3。由表3可以发现，基于Boltzmann动态模量主曲线构建得到的AC13-SBS、AC20-SBS两种沥青混合料的应变依赖模型，拟合的相关系数均高于97%，由此表明该模型可靠性较高，能够准确描述温度、频率以及应变水平对沥青混合料动态模量的影响。

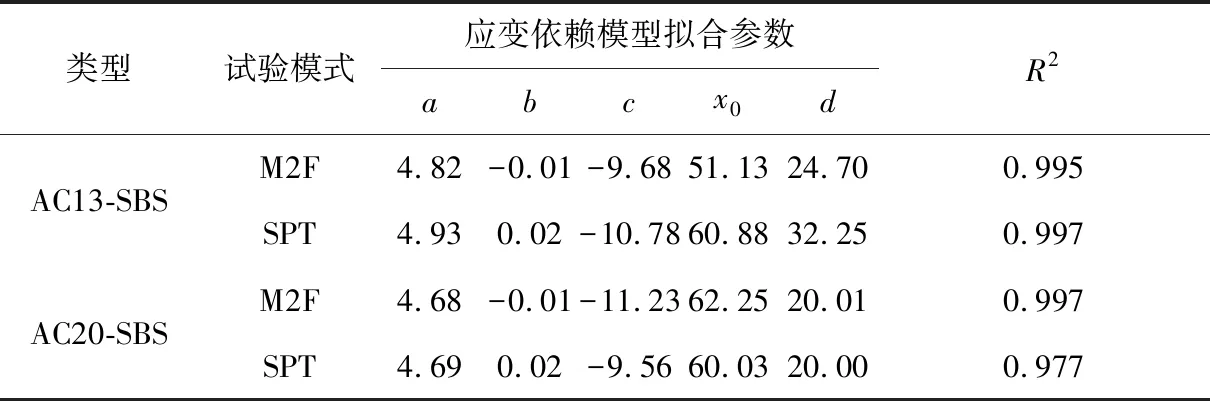
表3 沥青混合料应变依赖模型拟合参数Table 3 Fitting parameter of strain-dependent model

根据表3中拟合数据可绘制得到沥青混合料应变依赖模型，即沥青混合料主曲面，如图3、图4。

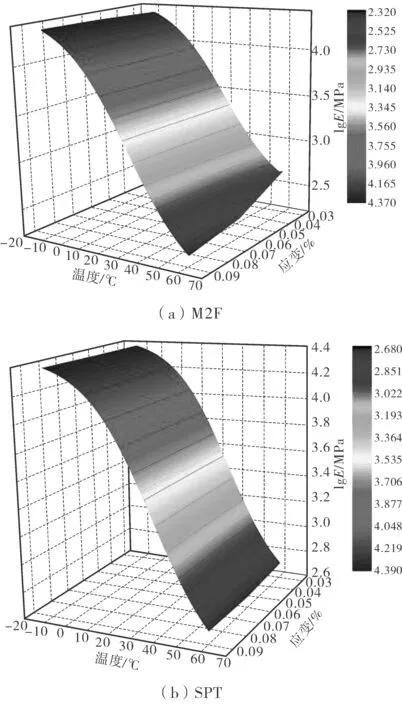
图3 AC13-SBS复数模量主曲面Fig. 3 Complex modulus master surface of AC13-SBS

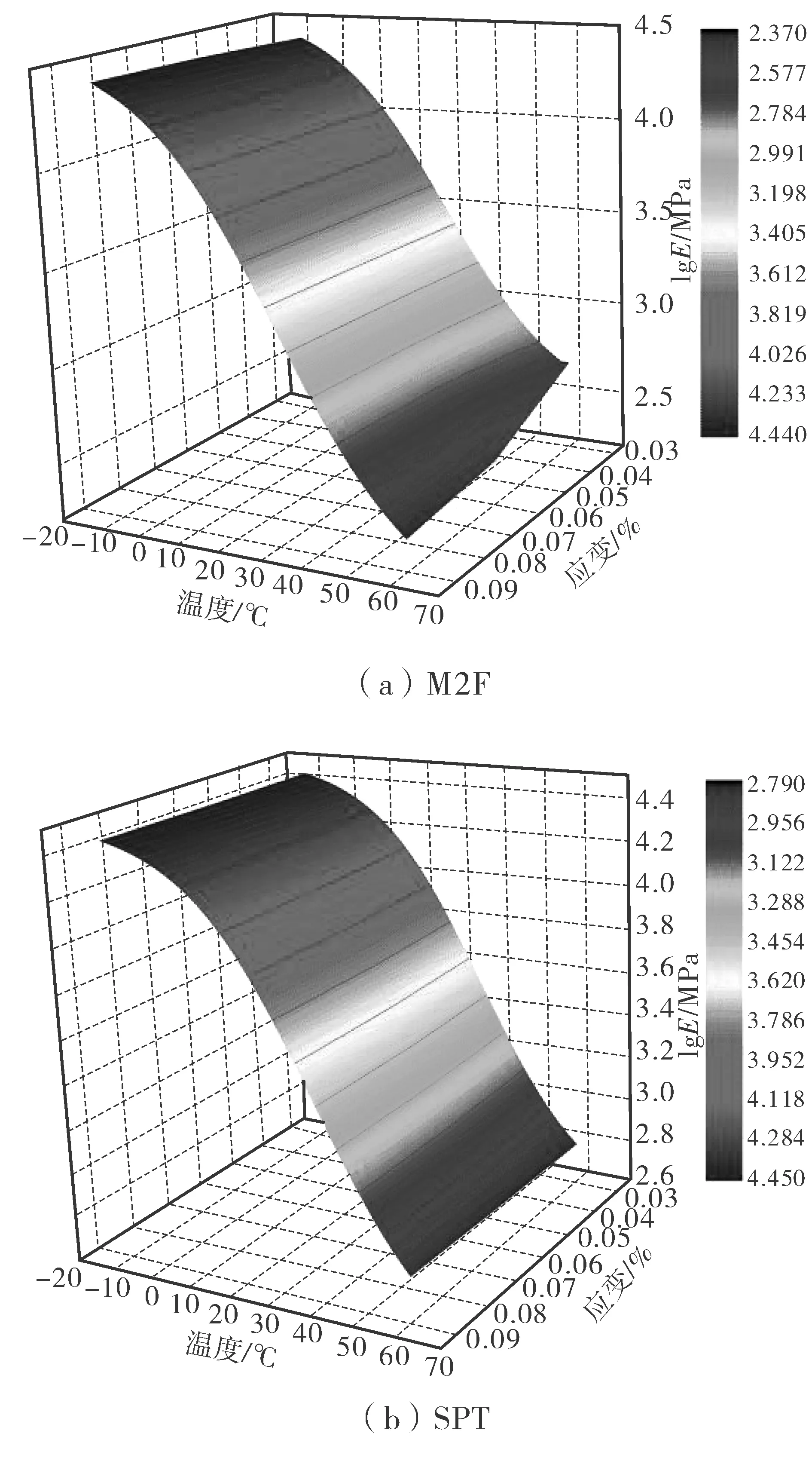
图4 AC20-SBS复数模量主曲面Fig. 4 Complex modulus master surface of AC20-SBS

综上所述，沥青混合料的动态模量不仅受荷载频率和温度的影响，应变水平对沥青混合料的力学响应状态也有明显的影响。沥青混合料的动态模量随着频率的增加而增加；反之则减小。荷载模式也是影响沥青混合料应变依赖特性的关键因素，材料在弯拉和压剪受力模式下应变模式不同。由于目前用于测量沥青混合料复数模量的方法较多，且不同模量测量方法下沥青混合料的受力方式不同，因此在进行结构设计和力学分析时，应建立沥青混合料在不同受力模式下的复数模量应变依赖模型。

4 结 论

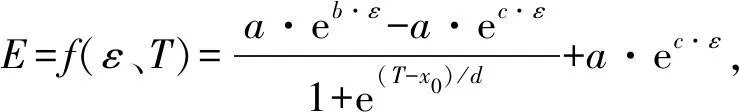
2)在不同的荷载模式下，沥青混合料复数模量均存在应变的依赖性，但是变化规律不同。在SPT试验中(压剪状态)，沥青混合料的动态模量随应变的增加而逐渐增大；在梯形梁试验中(弯拉状态)，沥青混合料的动态模量随应变的增加而逐渐减小，直至材料的破坏。

3)沥青混合料复数模量的应变依赖性受温度的影响比较显著。在低温区，沥青混合料复数模量的应变依赖性并不显著；当材料处于常温或者高温状态下，材料的应变依赖性逐渐增大，表明沥青混合料的非线黏弹特征越来越显著。

4)在相同应变水平下，压剪状态下测定的复数模量值高于弯拉状态，低频高温条件下此种差异更为显著。