光照强度与环境温度对光伏发电系统影响的研究

张唯一 张菁

摘 要：本文对新能源开发和利用过程中的光伏发电系统进行了深入研究。首先分析了最大功率点跟踪算法、PWM 斩波控制、蓄电池充放电原理等，并在此基础上构建了光伏系统的控制模块以及储能模块。然后根据建立的数学模型以及相关算法，搭建光伏发电系统的仿真模型，并分析在不同光照强度和环境温度下光伏发电系统的输出特性。

关键词：光伏发电系统;光照强度和环境温度;控制模块;储能模块

文章编号：2095-2163（2019）04-0297-04 中图分类号：TM715 文献标志码：A

0 引 言

光伏发电是缓解当前能源枯竭等一系列重大问题的最有效手段[1]。光伏发电系统由太阳能电池组件模块、控制模块、蓄电池储能模块等组成，电池模块是光伏发电系统中的核心模块[2]。光伏发电系统的性能受外部环境的影响[3]。建立一个准确、通用的光伏发电系统，观察其在不同环境（光照、温度等）下的输出特性，对进一步提高系统的效率具有重要意义[4]。

光伏发电系统的输出功率与运行点有关。用MPPT算法求出系统的最大功率点，可以提高系统的最大功率输出[5]。通过建立仿真模型，为今后光伏发电系统的实际建设和运行奠定了基础。

1 光伏发电系统控制模块模型

1.1 MPPT控制模块的搭建

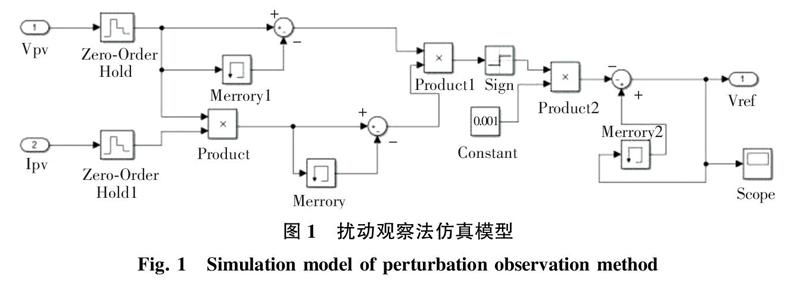
本次仿真 MPPT 算法采用的是扰动观察法，并在 MATLAB/Simulink 环境中对其进行了仿真，其模型如图1所示。

Zero-Order Hold是零阶保持器，其作用是对输出量进行采样，本次设计选用最大值0.0001;“Memory”是延时发生器，其输出是上一个采样期的输入值，并作为下个周期的比较量;“Sign”模块可以判断输入的正负，并且当输入大于 0 时输出 1，输入为 0 输出 0，输入小于 0 时输出-1，作用是把正弦、余弦函数变成方波输出。

1.2 PWM脉宽调制仿真模型

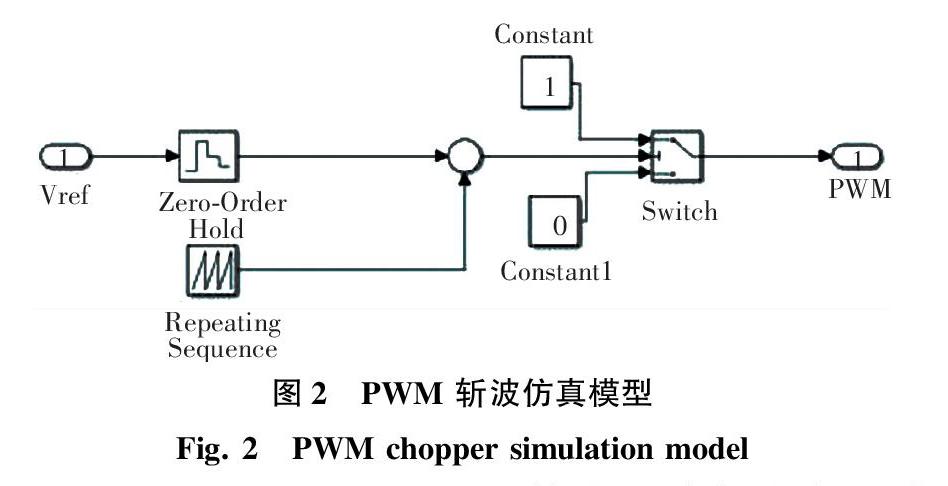
仿真采取的做法是通过 MPPT 得到追踪的参考信号，然后调制其波形，得到所希望的 PWM 調制波。常用的参考信号有锯齿波和等腰三角波，其中后者的应用更多一些。原理是，在交点时刻控制电路中可控开关器件的开断，通过这种方式能够得到宽度和信号波幅值成正比关系的脉冲。PWM斩波仿真模型如图2所示。

Repeating Sequence可以输出一个标准的三角波信号，与前级 MPPT 输出的比较差值，作为下一个模块的启动。Switch接受上级的输出结果并进行判断，若大于零则接通constant 1，若小于零则接通 constant 0，然后进一步驱动 DC/ DC 电路。

1.3 DC/DC 斩波电路仿真模型

通过控制功率开关的占空比α，就可以获取输出的最大功率点，也实现了MPPT 控制过程。DC/DC 变换电路常用的有升压 boost 电路和降压 buck 电路。

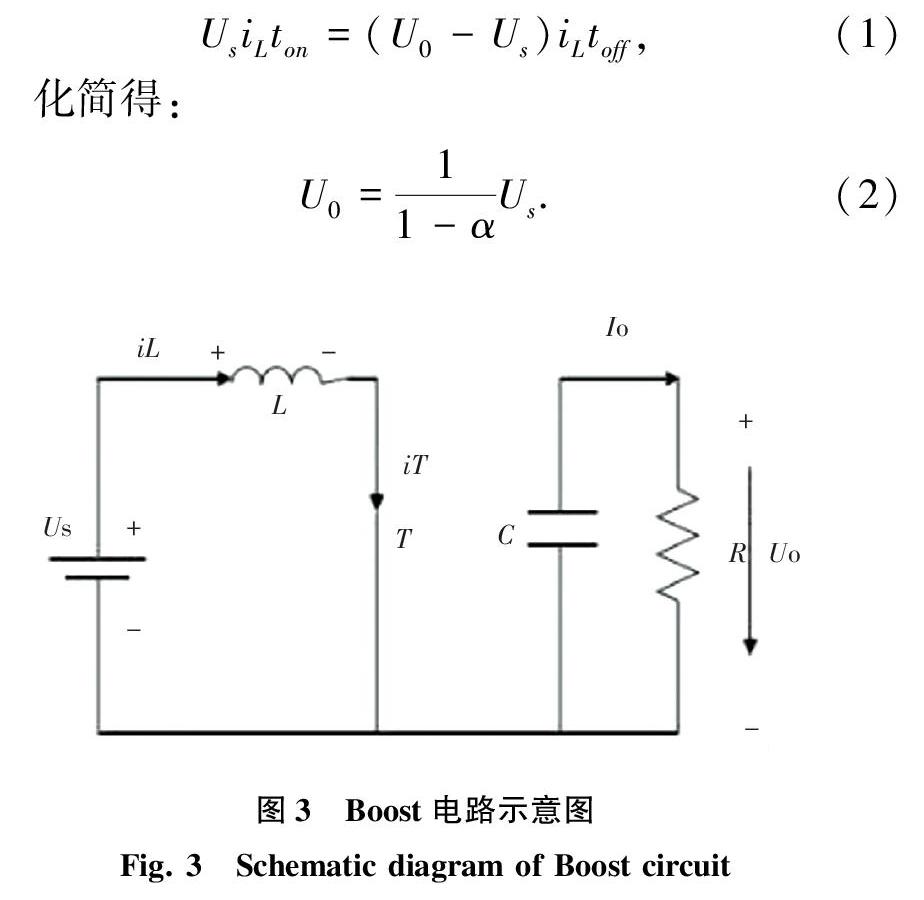
本模块采用 Boost 作为 DC/ DC 转换的直流升压电路，这种方式不仅能够大大改善工作效率，并且也使得电路驱动变得更加简单，因此利用 Boost升压电路DC/DC变换器的电路会有一个比较理想的

结果。图3所显示的就是 Boost 直流升压电路的运行状态：通过控制器调节 switch开关的占空比α，就可以得到理想的输出电压。

若电流的纹波幅度高，则电感可能在整个换向周期结束之前完全放电。在这种情况下，通过电感的电流在一段时间内下降到零，虽然差别很小，但其对输出电压方程式有很大的影响。电压增益可以用如下公式计算：

2 光伏发电系统仿真模型及特性分析

经过上述的设计，完成了对一个独立的光伏发电系统模型的搭建仿真。

下面对仿真进行以下说明：总系统的模型由多个子系统构成，其中包括太阳能光伏电池阵列、MPPT 控制器（包括 PWM 斩波、DC/DC 直流升压电路）和蓄电池组件。将每一部分进行封装，最后得到了一个独立的光伏发电系统模型，如图4所示。

根据商家给出的参数，设定电感值L=10·e-3H，电容值C=300·e-6F，等效负载R=20Ω，Diode 模块采用默认数据。本次设计中用到的太阳能光伏电池的参数见表1。

2.1 标准情况下的仿真分析

首先，在正常的外界条件下（太阳辐射强度Sref=1 000 w/m2，外界温度Tref=25 ℃）对建立好的模型进行仿真，观察在 MPPT 追踪前后的功率、电压仿真曲线，运行后的结果如图5，图6所示。

由图6 可知，本次设计中用到的直流升压电路的升压比为53.71/17.68≈3。

2.2 温度T发生变化时的仿真

太阳能光伏发电系统在实际运行过程中，一般放在室外，会受到周围环境温度的影响。每天早晚有一定的温差，每年的4个季节温度也不一样，所以本次设计基于不同温度条件下，进行了相应的仿真实验。环境温度数据见表2，仿真曲线如图7、图8所示。

根据仿真图可以看出，环境温度升高，系统的输出功率、电压等均会下降，然而环境温度降低时，光伏系统的输出量则会变多。不难看出，环境温度的改变与太阳能光伏发电系统的输出特性是成反比关系的。尽管如此，环境温度的改变对于系统输出特性的影响还是比较微弱的。

2.3 太阳辐射强度S改变时的仿真

太阳能光伏发电系统在实际运行过程中，一般放在室外，所以光照也会给其带来一定的影响，所以对 S 发生变化时进行仿真是有意义的，本次设计基于光照条件下，进行了相应的仿真实验。太阳辐射强度变化见表3。

光照量S对太阳能光伏发电系统输出特性的影响比较大，当光照量S变化很大（由1 000 w/m2→600 w/m2），且辐射强度不太高时，太阳能光伏系统的输出功率并不稳定，会跳动。根据实验可以推测，光照弱的地方，太阳能光伏系统的性能差，所以阴天、雨天等天气不利于系统运行。根据上下2条曲线对比可以看出，直流升压回路促进了输出的稳定性。

3 結束语

太阳能光伏电池输出与外界环境温度T和太阳辐照强度S具有明显的非线性特征，只有在特定的电压值下才有最大的输出功率，通过 MPPT 控制找到最大功率点有助于提高光伏发电的效率。

本文通过仿真搭建出来的光伏发电系统模型，验证了光伏发电的输出特性。在未来的研究中，可以尝试建立系统的实物模型，以便于更好地对新能源开发利用进行深入地研究。

参考文献

[1] 刘皓明， 宁健， 朱芳芳，等. 考虑随机性分布式电源的配电系统潮流计算[J]. 电力需求侧管理， 2014， 16（1）：11-14.

[2] 许洪华. 中国光伏发电技术发展研究[J]. 电网技术， 2007， 31（20）：77-81.

[3] 张立梅， 唐巍， 赵云军，等. 分布式发电对配电网影响的综合评估[J]. 电力系统保护与控制，2010，38（21）：132-135，140.

[4] 李晶， 许洪华， 赵海翔，等. 并网光伏电站动态建模及仿真分析[J]. 电力系统自动化， 2008， 32（24）：83-87.

[5] 王飞， 余世杰， 苏建徽，等. 太阳能光伏并网发电系统的研究[J]. 电工技术学报， 2005， 20（5）：72-74，91.

[6] 王成山， 郑海峰， 谢莹华，等. 计及分布式发电的配电系统随机潮流计算[J]. 电力系统自动化，2005，29（24）：39-44.

[7] 李振坤， 陈星莺， 刘皓明，等. 配电网供电能力的实时评估分析[J]. 电力系统自动化，2009，33（6）：36-39，62.

[8] 于雷， 王立地， 纪建伟，等. 基于PV节点分布式电源的弱环网潮流计算[J]. 沈阳农业大学学报， 2013， 44（3）：373-376.

[9] 谷文卓. 配电网最大供电能力的定义、模型与计算方法[D]. 天津：天津大学， 2012.

[10]陈浩， 张焰， 俞国勤，等. 配电网最大供电能力计算方法[J]. 中国电力，2009，42（8）：20-23.

[11]刘洪， 郭寅昌， 葛少云，等. 配电系统供电能力的修正计算方法[J]. 电网技术， 2012， 36（3）：217-222.

[12]国宗， 韦钢， 李明，等. 含分布式电源的配电网供电能力评估方法[J]. 现代电力，2015， 32（4）：56-61.

[13]YU B， MATSUI M， JUNG Y，et al. A combined active anti-islanding method for photovoltaic systems[J]. Renewable Energy，2008，33（5）：979-985.

[14]HUNG G K， CHANG C C， CHEN C L. Automatic phase-shift method for islanding detection of grid-connected photovoltaic interters[J]. IEEE Power Engineering Review，2002， 22（9）：55.

[15]YU G J， JUNG Y S， CHOI J Y，et al. A novel two-mode MPPT control algorithm based on comparatvie study of existing algorithms[C]//2002 Conference Record of the Twenty-Ninth IEEE Photovoltaic Specialists Conference .New Orleans， LA， USA：IEEE，2002：1531-1534.

[16]De CASTRO L N， Von ZUBEN F J. Learning and optimization using the clonal selection principle[J]. IEEE Transactions on Evolutionary Computation，2002，6（3）：239-251.

[17]De SOTO W， KLEIN S A. Improvement and validation of a model for photovoltaic array performance[J]. Solar Energy，2006，80：78-88.