基于悬架解耦遗传控制的车辆侧倾研究
何 锋,冯子航,2,吴 清
(1. 贵州大学 机械工程学院,贵州 贵阳 550025; 2. 江苏宿迁宿城经济开发区管理委员会,江苏 宿迁 223800;3. 北京理工大学 机械与车辆学院,北京100081)
近年来,车辆行驶稳定性逐渐成为研究的热点。车轮受到路面激励引起车辆的垂向、俯仰、侧倾运动是多输入多输出(MIMO)的耦合过程。其极大影响了乘坐的稳定性及舒适性,尤其在转向工况下,由侧向力引起的侧倾运动会增加车辆的不稳定性。许多车企基本都采用悬架、转向等系统对车辆稳定性进行控制,并且达到一定的控制目的[1]。
目前,国内不少学者针对整车悬架系统侧倾稳定性控制进行了研究。金智林等[2]以整车悬架为基础,分析了不同路面激励下非簧载质量对车辆侧倾稳定性的影响,并提出分层控制策略;王亚雄等[3]在考虑横向载荷转移率(LTR)、侧倾角加速度等因素的基础上,构建了3自由度主动悬架线性二次型高斯(LQG)控制器,但其侧倾运动主动悬架的控制加权系数难以确定;张亮修等[4]分别建立起3自由度侧倾动力学模型和7自由度垂向动力学模型来估计车辆的侧倾状态,并通过滑模变结构来决策车辆的侧倾力矩。但上述研究的控制方法都未涉及系统解耦,难以明确转向对侧倾的具体影响。陈建国等[5]在单轮激励模型基础上对整车悬架系统进行解耦控制,达到了一定效果,但没有明确其反馈控制器的二阶系数。
笔者在建立整车9自由度主动悬架系统的同时建立了四轮路面激励模型作为输入信号,运用微分几何解耦方法对整车悬架系统进行解耦,使得整车的垂向、俯仰、侧倾运动相互独立。并设计反馈控制器,通过遗传算法对控制器二阶方程系数进行全局寻优,对后续解耦后系统进行单独控制。结果表明:经解耦控制后悬架系统使悬架系统垂向加速度、侧倾角加速度均方根值大幅衰减,车辆稳定性大大提高。
1 主动悬架车辆侧倾模型
为研究转向工况下车辆主动侧倾问题,笔者建立了9自由度车辆侧倾模型,包括整车主动悬架的7自由度模型、以及线性2自由度车辆侧向动力学模型,如图1。
整车侧向运动平衡方程如式(1):
(1)
整车质心横摆运动平衡方程如式(2):
(2)
前后轮侧偏力[6]如式(3):
(3)
整车质心处簧载质量垂向运动方程如式(4):
(4)
整车悬架非簧载质量垂向运动方程如式(5):
(5)
整车质心处侧倾运动方程如式(6):
(6)
整车俯仰运动方程如式(7)、(8):
(7)
(8)
式中:m、ms、mui分为整车质量、簧载质量、非簧载质量;αf、αr分别为前后轮的侧偏角;Ix、Iy分别为整车绕x、y轴的转动惯量;Lf、Lr分别为质心到前后轴距离;c、d分别为质心到左右侧车轮横向距离;θ为簧载质量俯仰角;φ为簧载质量侧倾角;Zs为簧载质心垂向位移;Zri为路面不平度函数;Zui为非簧载质量垂向位移;Zsi为簧载质量垂向位移;Kti为轮胎刚度;Ksi为悬架弹簧刚度;Csi为悬架阻尼系数;Fai为作动器产生的力。
2 四轮路面激励建模
国内外关于整车转向工况下的研究,大多基于建立单轮路面激励模型。为提高车辆整车转向工况模型的准确性,考虑到基于滤波白噪声,笔者建立了单轮路面激励时域模型,并根据左右轮迹相干函数和前后轮的滞后性,建立四轮路面空间时域模型。
2.1 单轮路面激励时域建模
根据路面功率谱密度及系统频响函数建立单轮路面激励Z(t)的时域模型[7],如式(9):
(9)
式中:f0为下截止空间频率,f0=0.01 m-1;v为汽车行驶速度,m/s;G0(n0)为路面不平度系数,m3;Z(t)为随机路面激励;ω(t)为均值为0、功率谱密度为1的理想单位白噪声。
2.2 四轮路面激励时域建模
车辆行驶过程中,左、右轮受到的随机路面激励并不相同,一般采用相干函数或者传递函数进行描述,文献[8]则选择了相干函数作为激励信号的数学模型,如式(10):
(10)
式中:n为空间频率;B为左右车轮轮距;α为路面同性指数;W为频率梯度;np为参考空间频率;P为梯度指数。
假设车辆匀速行驶,车辆后轮所受路面激励相较于前轮会产生时间为T的延时,如式(11):
T=(Lf+Lr)/v
(11)
假设车辆行驶在B级路面,速度为v=20 m/s。由式(9)~(11)则可建立起四轮路面激励时域模型,如图2~5。由图2~5可看出:整车模型在单轮激励和四轮激励条件下,各个输出参数均方根值有很大变化。与单轮激励相比,四轮激励下的垂向加速度均方根值(RMS)增加了13%;侧倾角超调量增加了33%。
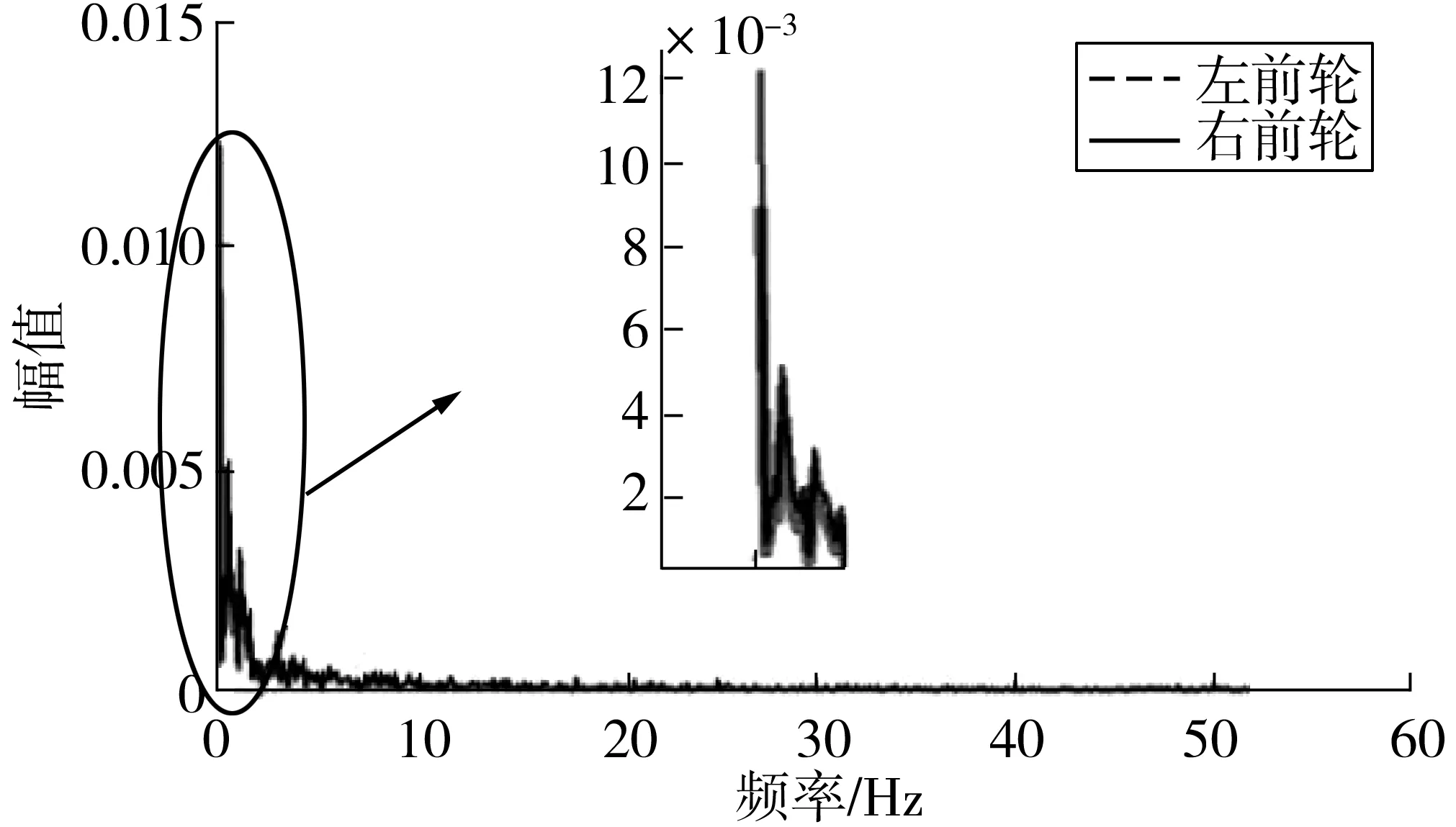
图3 前轮激励频域Fig. 3 Front wheel excitation frequency domain

图4 垂向加速度对比Fig. 4 Vertical acceleration comparison
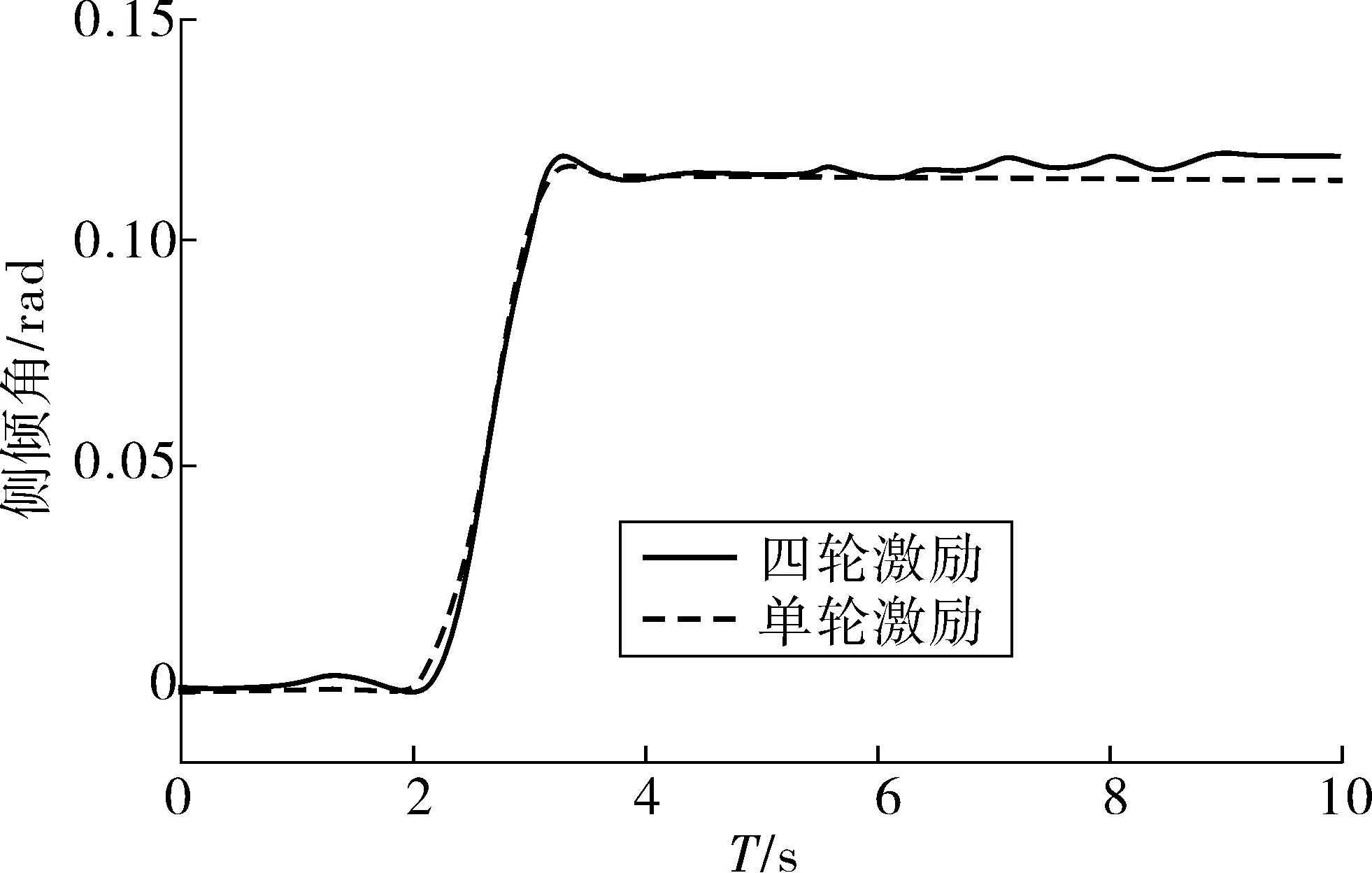
图5 侧倾角对比Fig. 5 Roll angle comparison
3 微分几何悬架解耦
3.1 非线性化二阶系统解耦条件
将悬架系统建成18维状态方程组[9],MIMO非线性系统表达如式(12):
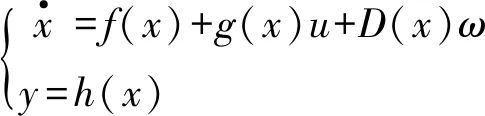
(12)
式中:x=[x1,x2,…,x18]∈Rn为系统状态变量;u∈Rm为控制变量,由作动器输入;ω=[Zr1,Zr2,Zr3,Zr4,δ]∈Rl为外界干扰信号;h(x)=[Zs,θ,φ,Zu1]为输出信号;f、g、D分别为非线性光滑向量场。
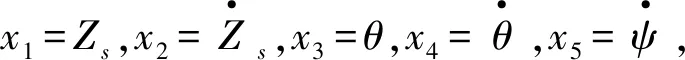
引入状态反馈控制规律,如式(13):
u=α(x)+β(x)ϑ(x)
(13)
式中:α为m维的解析向量;β为邻域内的m维解耦逆矩阵;ϑ为新的输入变量。
根据文献[10],MIMO非线性系统在x0处具有关于输入μ向量相对阶r=[r1,r2,r3,r4]。
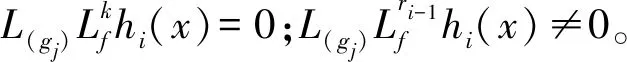
2)m×m解耦矩阵为:
E(x)=
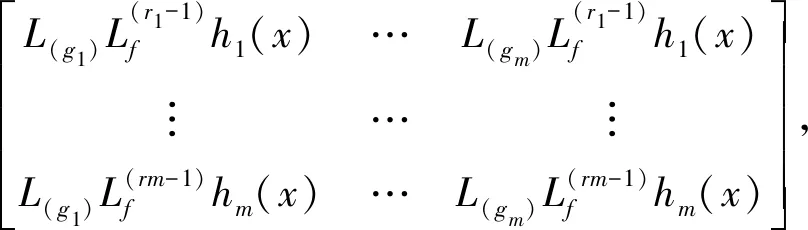
3.2 悬架系统解耦控制计算
根据李氏函数规则有:
⋮
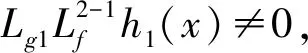
系统的解耦矩阵E(x)可表示如式(14):
(14)
经计算:detE≠0;LDLfhi(x)=0,i=1,2,3,4。根据文献[11],反馈控制规律的反馈形式如式(15):
(15)
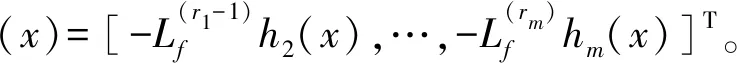
3.3 控制量计算
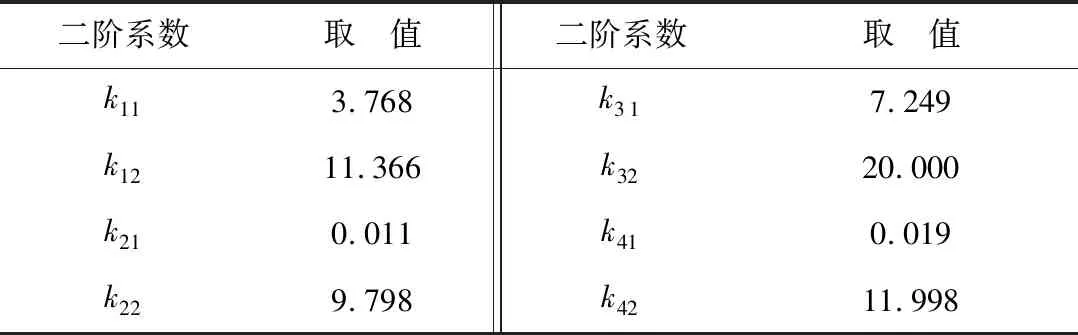
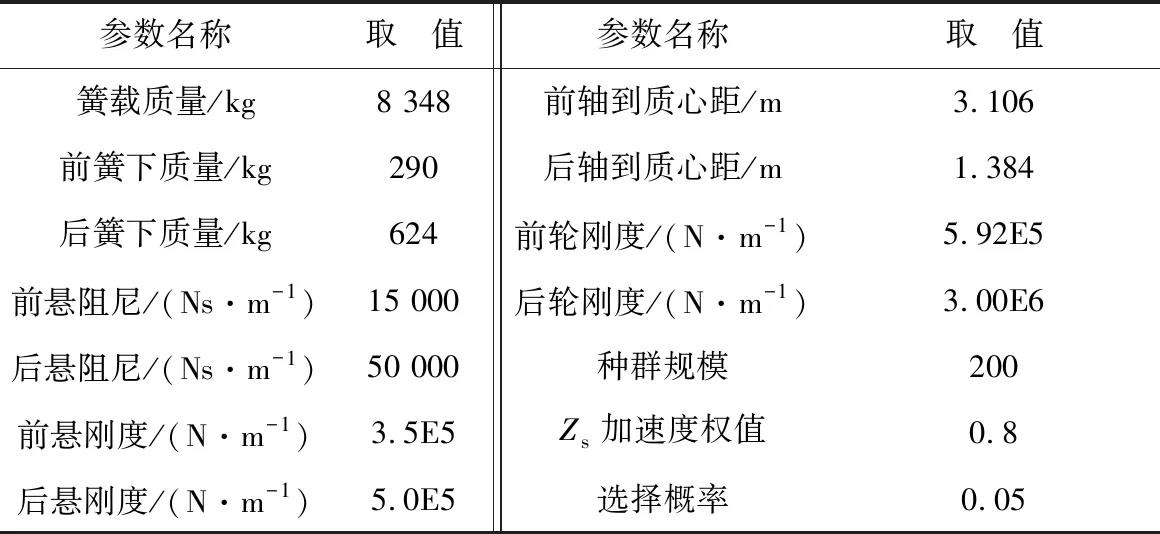
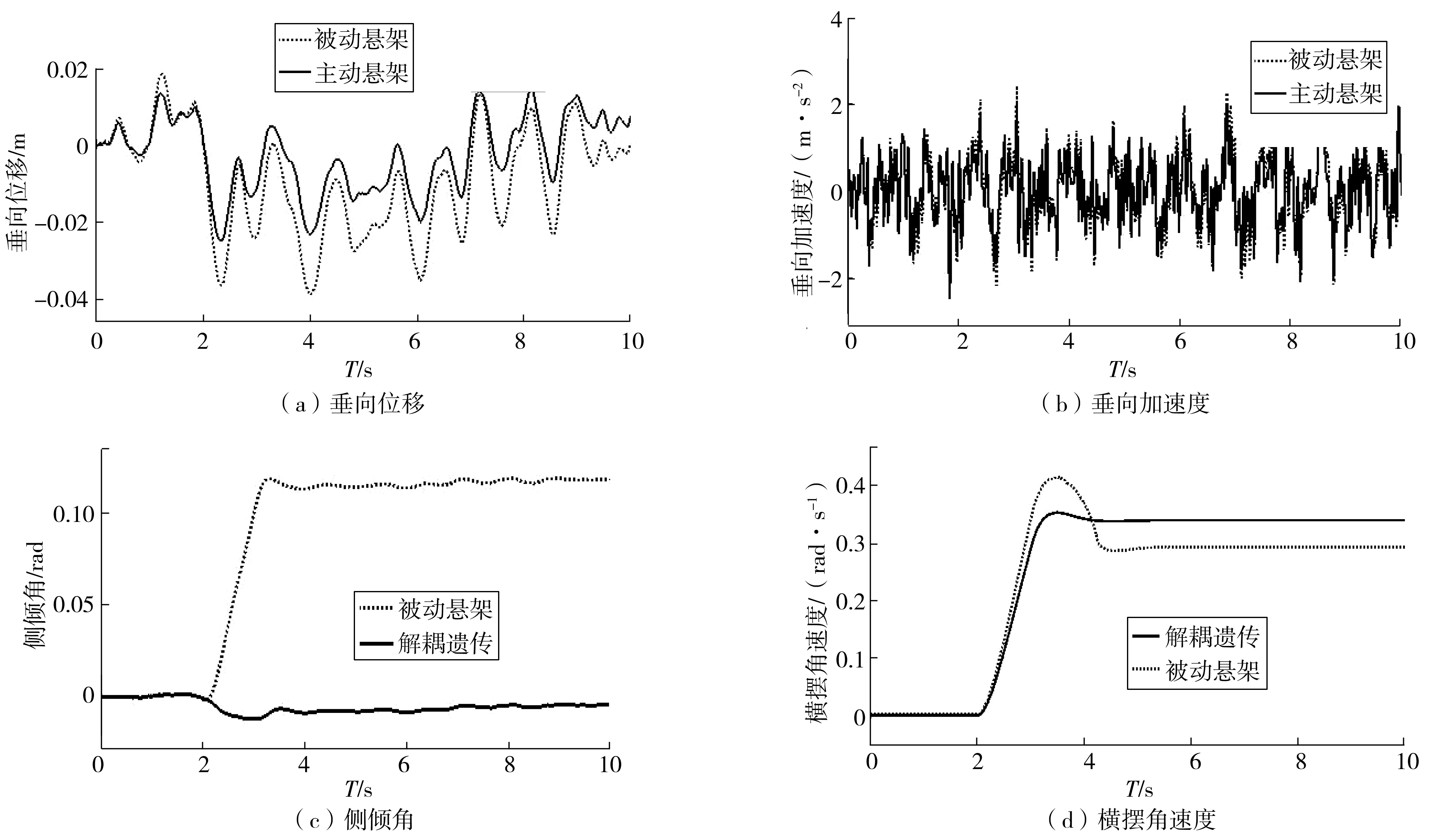
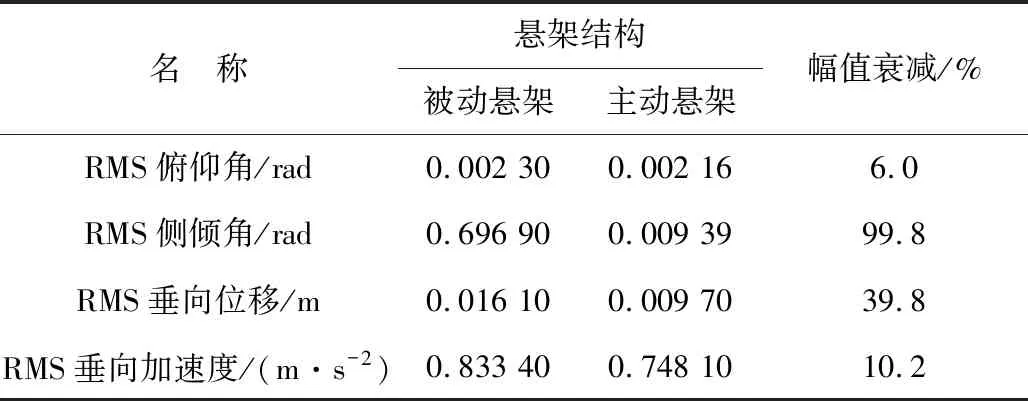
当系统相对阶r (16) 式中:k11、k12分别为参考出入中垂向速度、垂向位移相关的系数;k21、k22分别为与俯仰角速速、俯仰角相关的系数;k31、k32分别为与侧倾角速度、侧倾角相关的系数;k41、k42分别为与非簧载质量垂向位移相关的系数。 为此,式(16)中ϑ3的表达式可表示如式(17): (17) 把式(13)~(16)带入式(12)中,将垂向位移加速度等转换为独立的线性二阶系统,如式(18): (18) 根据劳斯判据可知:二阶系统稳定的充要条件是各项系统系数都大于0,但系数选取的不同也会直接影响到各个参数变化。 将四轮路面激励信号和前轮转向角作为目标优化的输入信号。式(1)~(8)编写为18元微分方程组,并作为子m文件导入到MATLAB中,运用四阶Runge-Kutta将式(12)方法编写为母m文件进行调用求解。经计算仿真采用步长为h=2.5E-04。 为减少车辆行驶过程中悬架振动问题,对垂向位移加速度等重要参数进行加权处理[12]。多目标遗传算法优化目标函数如式(19): (19) 根据劳斯判据:系统稳定条件为kij>0。由于车辆性能指标之间存在的矛盾,k值选取不同会直接影响悬架目标输出参数。笔者设定kij的变化范围为0~20。 笔者运用遗传算对目标函数式(19)进行优化求解,其反馈控制二阶系数结果如表1。 表1 反馈控制二阶系数Table 1 Second order coefficient of feedback control 仿真过程中的模型参数如表2。根据已建立的模型和算法,笔者选择B级路面,车速设定为20 m/s,在第2 s时刻方向盘转角由0°转到150°,并保持该角度不变。通过MATLAB/Simulink进行仿真对比分析,其仿真结果如图6。 表2 仿真主要参数Table 2 Main parameters for simulation 图6 仿真结果Fig. 6 Simulation result 由图6可知:经解耦控制后的整车悬架垂向位移、垂向加速度得到了抑制,同时整车横摆角超调量也大幅减小。基于数学模型,笔者分析了转向角对车身侧倾的影响,并加入相应的衰减项进行控制,车身侧倾角大幅衰减,得到了很好控制,说明该控制方法可行有效,如表3。 表3 结果比较Table 3 Comparison of results 1)建立了整车9自由度侧倾模型和四轮路面激励模型,并对比分析了单轮和四轮激励对整车垂向加速度和侧倾角的影响。 2)在转向工况下,通过数学模型分析了前轮转角对车辆侧倾角的影响,并在反馈控制中加入了相应的衰减项。 3)针对解耦算法中反馈控制器二阶系数选取的复杂性,运用遗传算法对目标函数进行全局寻优,最后通过MATLAB/Simulink进行仿真验证。结果表明:在转向工况下,所使用的解耦遗传算法能使车辆稳定性得到提高。
4 反馈控制二阶系数优化
4.1 目标函数
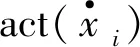
4.2 优化结果与分析
5 仿真分析
6 结 论

