静电纺丝聚合物纳米纤维力学性能表征及凝聚态结构研究进展

张德立　喻进华　田厚宽

摘 要：聚合物纳米纤维由于其独特的纳米结构和性能特征，在膜材料、生物医用材料等领域具有广阔应用前景。静电纺丝技术是制备聚合物纳米纤维的最有效方法，已获得了广泛应用。作为纤维材料，力學性能是其最重要的物理性能之一。然而，因其尺寸极其微小，聚合物纳米纤维力学性能表征非常困难。近十多年来，科学家开展了系列研究，获得了关于静电纺丝聚合物纳米纤维结构与力学性能的重要研究成果。由于纳米受限等的影响，静电纺丝纳米纤维具有与普通纤维不同的力学性能特征与凝聚态结构。文章综述了表征单根聚合物纳米纤维力学性能的方法，总结了纳米纤维力学性能与其尺寸的依赖关系，简要介绍了描述静电纺聚合物纳米纤维聚集态结构模型，并对纳米纤维结构与性能关系研究进行了展望。

关键词：聚合物纳米纤维;力学性能;凝聚态结构;尺寸依赖性

中图分类号：TS101.921;TB303

文献标志码：B

文章编号：1009-265X（2019）03-0010-06

A Review on Mechanical Properties of Electrospun PolymerNanofibers： Characterization and Condensed Structure

ZHANG Deli1， YU Jinhua2， TIAN Houkuan3

（1.Chongqing No.1 Middle School， Chongqing 400030， China; 2.College of Textile Garment，Southwest University， Chongqing 400715， China; 3.School of Pharmaceutical andChemical Engineering， Taizhou University， Taizhou 318000; China）

Abstract：Because of its special structures and performance characteristics， polymer nanofiber is widely used in the field of membrane material and biomedical materials. Electrospinning is the most effective way to prepare polymer nanofibers， and has been widely applied. As a fibrous material， its mechanical property is one of the most important physical properties. However， the characterization of mechanical properties of polymer nanofibers is very difficult due to the nanoscale size. In the recent decade， scientists have carried out a series of studies and gained important research achievements about the structure and mechanical properties of electrospun polymer nanofibers. Due to the impacts of nano limit， electrospun nanofibers own different mechanical properties and condensed state structure from common fibers. The methods for characterization of mechanical properties of single polymer nanofiber were summarized， and the dependence relationship between mechanical properties of nanofibers and the size was summed up in this paper. Meanwhile， several theoretical models describing the condensed structures of polymer nanofibers were introduced. In the end， the research prospects on the relationship between nanofiber structure and properties was also discussed.

Key words：polymer nanofibers; mechanical properties; condensed state structures; size dependence

聚合物纳米材料因其独特的物理化学性质受到广泛关注。目前，人们已经能够制备直径为几十纳米的聚合物纤维[1-2]。这种纳米纤维被广泛应用于生物材料、药物载送、能量储存与转换、传感、超滤、微滤等领域[3-4]。静电纺丝技术是目前使用最普遍的聚合物纳米纤维制备方法，可实现纳米纤维直接、连续制备与生产，受到了广泛研究。值得注意的是，大量研究发现静电纺丝制得聚合物纤维分子链的构象、聚集态结构以及力学性质显著不同于宏观尺度下的性能，呈现出尺寸依赖性[5-6]。深入研究静电纺丝聚合物纳米纤维结构与性能的关系对于功能性纳米材料的结构设计和性能优化具有重要指导意义。然而，由于纳米纤维尺寸微小，表征宏观尺寸聚合物材料力学性能的方法并不适用于纳米纤维，因此聚合物纳米纤维结构模型的建立具有很大的挑战。近十多年来，在工作测量静电纺丝聚合物纳米纤维的力学性能及黏弹性方面，科学家开展了系列创新研究工作，获得了重要进展。本文将对静电纺丝单根纳米纤维力学性能表征以及纳米纤维聚集态结构模型进行综述，并对静电纺丝纤维结构与性能关系研究进行了展望。

1 聚合物纳米纤维制备及其力学性能表征重要性

目前纳米纤维的制备方法有很多，例如纺丝法[7]、模板合成法[8]、相分离法[9]、自组装法[10]以及静电纺絲法[11-12]等。相对于其他方法而言，静电纺丝法具有设备简单、操作方便、纤维形态/尺寸可控性好、适用性广泛等优势，是制备大量聚合物纳米纤维最有效的方法。同时，利用静电纺丝法制备的聚合物纤维具有广泛的应用前景，如用作增强纤维、分离膜材料、传感器、药物传输、伤口敷裹材料以及纳米器件等[13]，因而受到了材料科学家的关注。

静电纺丝是一种基于高压静电场下导电流体产生高速喷射的原理而发展来的技术。静电纺丝过程中，将聚合物溶液通过一定速率从针尖匀速挤出。电场作用下，针头处的液滴由球形变为圆锥形（即“泰勒锥”），并从圆锥尖端不断延展得到纤维细丝。由于纳米纤维携带过量电荷的相互排斥作用，纳米纤维迅速发生弯曲，而后沉积在接收装置上，获得无纺布形式的聚合物纤维[14]。通过改变电压、收集装置类型、聚合物溶液性质（浓度、导电性、黏度、表面张力、溶剂的挥发性等）可以调控纤维的形态及结构，实现对聚合物纤维相关物理性能的控制。

聚合物纤维的力学性能是影响其在材料领域实际应用的重要因素。例如，超高模量、超高强度聚合物纤维在特种材料、军工、航空航天等领域具有重要应用价值，一直是材料科学家长期追求的目标。显然，以纤维为基础构建的功能材料的整体性能由单根纤维的物理特性所决定。因此，研究单根聚合物纳米纤维力学性能的基本规律，对于阐明聚合物纤维结构与性能关系、优化纳米纤维制备条件、生产工艺显得尤为重要。同时，由于力学性能是材料凝聚态结构及分子运动的体现，研究单根纤维力学性能还为纤维分子链排列方式、聚集态结构及分子运动的研究提供重要方法和手段。然而，由于纳米纤维尺寸极其微细，基于宏观材料开发的常规力学性能表征手段无法适用于纳米纤维的测量，制约了对聚合物纳米纤维力学性能及其与分子结构关系的研究。

近三十年来，随着纳米技术的发展，一大批新型纳米表征技术，例如原子力显微镜（AFM）、扫描电子显微镜（SEM）相继被开发出来。这为聚合物纳米纤维力学性能以及纤维分子链凝聚态结构的研究提供了新的契机，其研究结果对于高性能聚合物纤维材料的制备和开发无疑具有极其重要的价值。

2 聚合物纳米纤维力学性能的表征

由于原子力显微镜（AFM）能够对纳米尺度材料进行有效操控，使其成为了表征聚合物纳米纤维力学性能的最有效方法。1999年，Salvetat等[15-16]首次利用AFM对碳纳米管的弹性模量和剪切模量进行了直接表征，开启了利用AFM表征纳米纤维力学性能的大门。2005年，Bellan等[17]将该方法应用于静电纺丝聚乙烯纤维力学性能的表征。此后，大批科学家进入该研究领域，发展了系列方法研究聚合物纳米纤维力学性能。总的来说，目前基于AFM的纳米纤维力学性能表征技术主要有以下4种：单纤维拉伸测试技术、弯曲测试技术、纳米压痕技术、剪切调制原子力显微镜技术（SMFM）。

利用单纤维拉伸测试技术可获得单根纤维的“应力-应变”曲线。借助扫描电子显微镜（SEM）或者光学显微镜，将单根纳米纤维的两端分别粘接在AFM探针和一根金属线上。测量过程中，固定AFM探针，拉动金属线，使纳米纤维发生伸长直至最终断裂，如图1所示[18]。拉伸过程中，纤维所受应力（γ）可通过AFM悬臂梁的偏折度（δ）进行表征（γ=kδ;k为探针的弹性系数）[19]。纳米纤维的伸长则可利用SEM直接获得，从而得到单根纤维完整的“应力-应变”曲线，可获得拉伸强度和模量等信息。

弯曲测试技术[20]能够测量单根纳米纤维的刚性和模量。图2给出了常见的三点弯曲测试的实验构造图。首先将纳米纤维安放在微米/纳米栅格上，其形貌、位置、直径可通过原子力显微镜成像获得，如图3所示。测量时，在AFM探针上施加一定载荷（F）挤压纳米纤维，使纳米纤维产生形变（δ）。形变量δ则包含了纤维材料模量信息。根据弯曲理论，假设纳米纤维的形变是完全弹性的，并忽略AFM探针和纳米纤维之间的剪切力，基于三点弯曲测试的形变模型（式（1））[10]可以直接计算得到纳米纤维的杨氏模量（E）。

E=FL3/192δI    （1）

式中：I=πd4/64，d为纤维直径，各参数物理意义见图2。

Tan等[20]利用该法研究了单根聚乳酸纤维的力学性能，发现纤维模量随纤维直径减小而增大。

纳米压痕技术[21]和剪切调制AFM[22-23]也可表征纳米纤维力学性能，但需注意，这两种方法得到的模量为纤维表面层的模量。纳米压痕测试过程中，利用AFM针尖挤压纤维表面，通过监测针尖逼近纤维表面而后撤回过程中，针尖所受力的大小（F）和针尖与样品表面位移（D）的关系，可获得反映纤维表面力学性能信息的F-D曲线[24]，如图4。图4中虚线部分为针尖逼近样品表面过程中针尖受力（F）与针尖-表面相对位移（D）的关系曲线;实线部分为针尖回撤过程所获得F-D曲线。其中虚线中F随D减小而线性增大部分（图4中的C部分）的斜率可反映纤维表面硬度，该值越大则说明材料表面越硬、模量越高;图4中虚线和实线围成的面积则反映了纤维形变过程中的能量耗散，是表征纤维黏弹性的主要指标。

剪切力调制显微镜（SMFM），通过在水平方向上施加周期性震荡[26]，使针尖在样品表面平行滑动;并施加垂直方向的恒定载荷以维持针尖与样品表面的接触;测量平行方向悬臂振幅的变化（ΔX）可以反映样品表面的力学性能。当材料表面硬度较高时，针尖很浅地插入样品表面，造成小的接触面积和样品对针尖很小的拖拽力，最终导致较小的ΔX值。反之，当纤维表面变软，针尖插入表面较深，样品对针尖的作用力增大，使得针尖滑动的阻力变大，悬臂振幅变化值也增大。此外，利用Hertz模型还可计算得到纤维表面的剪切模量。Liuy等[27]利用SMFM研究了聚乙烯-聚乙酸乙烯酯共聚物和聚乙烯纤维表面弹性模量，结果发现当纤维直径小于10 μm后，其弹性模量随纤维直径减小而增大。

诸多学者利用上述方法对聚合物纳米纤维力学性能进行了研究，发现纤维弹性模量强烈依赖于其直径。2004年，Tan等[20]第一次研究了聚乳酸（PLA）纳米纤维的模量随纤维直径的变化，发现当纤维直径小于350 nm后，纳米纤维的杨氏模量随直径的下降而显著升高。随后，Wong等[28-30]针对这一特殊现象开展了系统研究，发现纤维弹性模量降低的现象与聚合物纤维种类、纳米纤维形成条件等无关，比如采用不同浓度聚合物溶液、不同静电压等。这说明聚合物纳米纤维弹性模量的尺寸依赖性是普遍现象，反映了静电纺丝聚合物纳米纤维截然不同的物理性质及凝聚态结构。

3 聚合物纳米纤维聚集态结构模型

聚合物材料弹性模量主要与其分子链结构相关。纳米纤维模量与尺度的依赖性则预示着纤维内高分子链具有与本体不同的聚集态结构。尽管，目前对于如何理解纳米纤维模量的尺寸依赖性并没有统一认识，但是大多数研究结果显示这一现象与高分子链取向有关。最简单的模型就是分子链在纤维中均匀取向;并且直径越小，取向度越高，从而导致模量增大。但是实际情况更加复杂，笔者总结了目前认可度较高的描述静电纺丝聚合物纳米纤维的三种微结构模型。

3.1 表面取向层模型（Surface Oriented Layer）

Ji等[31]利用三點弯曲测试和SMFM研究了单根聚苯乙烯（PS）纳米纤维的模量随直径的变化，发现两种测量方法所得的结果一致。根据前面对三点弯曲测试和SMFM技术的介绍，可知三点弯曲测试结果主要反映整根纳米纤维的模量;而SMFM得到纤维表面模量。Ji等[31]的实验结果表明整根纤维的模量与纤维表面的模量是一致的。基于该实验现象，作者提出表面取向层模型：认为在静电纺丝过程中由于表面张力的作用，导致纳米纤维存在一层分子链高度取向的表面层，具有较高的弹性模量。当纳米纤维直径较大时，表面层在整个纤维中所占体积分数非常小，纳米纤维的模量趋于本体材料值。然而，当纳米纤维直径减小，纳米纤维的高度取向表面层占整根纤维的体积分数越来越大，直到整根纳米纤维只由表面层组成，使得纳米纤维模量增加。此外，纳米填充聚合物复合纤维材料具有较高模量的实验现象也可用该模型解释。由于填充物/聚合物界面区域分子链取向度增大，导致纳米纤维复合物的模量高于普通的纳米纤维。

3.2 核-壳结构模型（Core-Shell Morphology）

Reneker等[32-33]发现纤维表面的双折射现象比纤维内部明显，表明纤维表面层分子链取向更显著。基于该现象，作者提出静电纺丝聚合物纳米纤维的核-壳模型。认为纳米纤维表面存在密度较高、高度取向的壳层。其认为，由于在成型过程中，纤维表面溶剂蒸发很快、分子来不及松弛，导致其表面附近分子链堆积更紧密、取向度更高。该模型可以通过研究成型溶剂挥发速率的影响进行验证。Koombhongse等[34]在对溶液质量分数为10%的聚醚酰亚胺-六氟异丙醇溶液进行静电纺丝时发现其只能得到中空的、塌陷形成带状的纤维[35]。这是由于六氟异丙醇挥发速率极快，导致纤维表面瞬间干燥、固化，纤维内部分子链、溶剂等不断往表面迁移，形成中空纤维。作者认为这是核-壳模型的极限情况，其结果也为核-壳结构模型提供了证据。

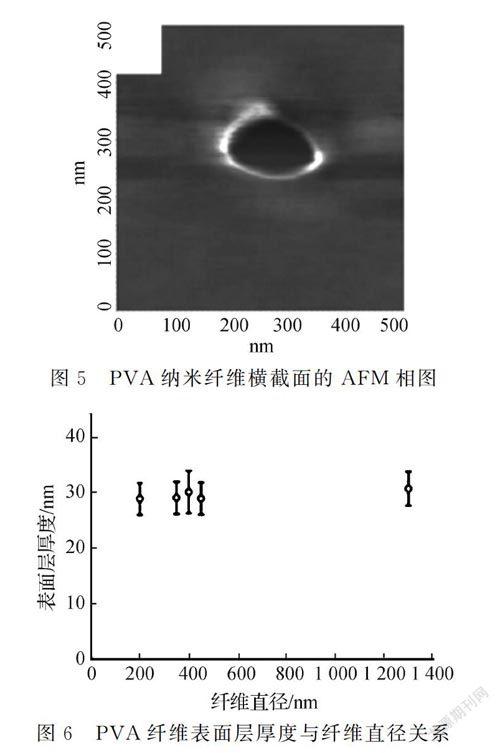
Guenthner等[36]利用计算机模拟研究了静电纺丝过程中纳米纤维的形成过程。结果发现，当溶剂挥发很快时，在纳米纤维表面层存在一层密度较高的壳层，壳层内基本不存在溶剂;而在纤维内部（核层），溶剂所占的体积分数超过80%。这在理论角度证明了核-壳结构的合理性。Stachewicz等[37]最近也给出了证明核-壳结构的强有力证据。作者利用聚焦离子束切断聚乙烯醇（PVA）纳米纤维，利用AFM对纤维横截面进行扫描。图5为PVA纤维截面区域的相图[36]，可以明显看到纤维边缘存在一圈亮度较高的区域。根据AFM理论，相图主要与材料软硬度相关。图5纳米纤维表面的亮色区域则表示纤维表面存在一层硬度较高的表层。作者统计发现不同直径PVA纤维表面壳层的厚度均为30 nm，见图6[36]。因此，这些结果充分支持了核-壳结构模型;认为纳米纤维是由分子链高度取向、高密度堆积形成的壳以及低密度、分子链无规排布的核组成。

3.3 无定形超分子取向结构模型（Formationof Supramolecular Oriented Amorphous-Structures）

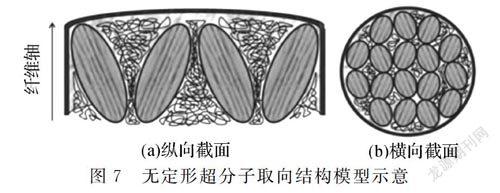
无定形超分子取向结构模型于2007年由Arinstein[30]首次提出。无定形超分子取向结构模型认为在静电纺丝过程中，由于受到快速拉伸作用，纳米纤维内部会形成分子链局部取向，类似超分子有序组装体的微小区域（如图7中的椭圆结果[38]）。超分子取向结构具有一定特征尺寸，当纳米纤维直径小于该尺寸后，由于受到纤维尺寸限制作用，超分子结构被迫沿着平行于纤维的方向进行规整排列，形成长程有序的规整取向结构，进而使得纳米纤维的模量升高。值得注意的是，超分子取向结构的尺寸与分子量相关，因此该模型也可用来解释纳米纤维临界直径的分子量依赖性。

需注意的是，上述纳米纤维结构模型都是指无定形纳米纤维或半结晶纤维中无定形部分的结构模型，未考虑结晶的作用。其中，表面取向层模型和核-壳模型都是基于表面效应，认为纳米纤维都存在高度取向的表面层。尽管均可解释部分实验现象，这些模型还是各存缺陷。例如，核-壳模型认为壳层的模量比纳米纤维高，但实验数据并不支持这一点[31]。另外，实验发现当纤维直径小于10 μm时，纳米纤维的模量便开始升高，这很难与“表面”模型统一。由于表面层厚度很薄（一般为几十纳米），很难想象超薄表面层会对数百纳米直径纤维性能产生影响。相比较而言，超分子取向结构模型可将更多实验结果统一，被认为可能是更接近实际情况的模型。

4 总结和展望

本文主要着眼于静电纺丝单根聚合物纳米纤维，介绍了纳米纤维力学性能的表征手段、纤维力学性能与尺寸的依赖关系。并在此基础上，总结了描述静电纺丝聚合物纳米纤维聚集态结构的几种模型。可以发现，聚合物纳米纤维具有与宏观材料截然不同的物理性能，其弹性模量随纤维直径减小而升高。显然，要实现对聚合物纳米纤维材料的制备、生产、结构优化等必然要求对其特殊结构与性能关系的深入理解。尽管目前提出的描述聚合物纳米纤维结构的3种模型可解释部分实验现象，然而各模型结果存在一定不足之处。从以上讨论可知，目前对于非晶态聚合物纳米纤维结构争论的焦点在于分子链局部有序的程度以及有序区域的分布。然而，直接测量纤维分子链局部取向还极其困难，造成目前人们并未获得对纳米纤维凝聚态结构及其性能关系清晰、统一的物理图像。近年来新表征技术的发展将有利于人们进一步深入认识聚合物纳米纤维的微观结构，最终实现对聚合物纳米纤维结构和物理性能的精确调控。

參考文献：

[1] RENEKER D H， CHUN I. Nanometre diameter fibres of polymer， produced by electrospinning[J]. Nanotechnology，1996，7（3）：216-223.

[2] LI D， XIA Y. Electrospinning of nanofibers： reinventing the wheel？ [J]. Advanced Materials， 2004，16（14）：1151-1170.

[3]YANG F， MURUGAN R， WANG S，et al. Electrospinning of nano/micro scale poly （L-lactic acid） aligned fibers and their potential in neural tissue engineering [J]. Biomaterials， 2005，26（15）：2603-2610.

[4] DING B， WANG M， WANG X，et al. Electrospun nanomaterials forultrasensitive sensors [J]. Materials Today， 2010，13（11）：16-27.

[5] PERKIN S， KLEIN J. Soft matter under confinement [J]. Soft Matter， 2013，9（44）：10438-10441.

[6] ALCOUTLABI M， MCKENNA G B. Effects of confinement on material behaviour at the nanometre size scale [J]. Journal of Physics： Condensed Matter， 2005，17（15）：R461-R524.

[7] ONDARCUHU T， JOACHIM C. Drawing a single nanofibre over hundreds of microns[J]. Europhys Lett， 1998，42（2）：215-220.

[8] FENG L， LI S， LI H，etal. Super-hydrophobic surface of aligned polyacrylonitrile nanofibers[J]. Angewandte Chemie International Edition， 2002，41（7）：1221-1223.

[9] MA P X， ZHANG R. Microtubular architecture of biodegradable polymer scaffolds[J]. J Biomed Mat Res， 2001，56（4）：469-477.

[10] WHITESIDES G M， GRZBOWSKI B.Self-assembly at all scales [J]. Science， 2002，295（5564）：2418-2421.

[11] DREW C， LIU X， ZIEGLER D， et al. Metal oxide-coated polymer nanofibers[J]. Nano Letters， 2003，3（2）：143-147.

[12] BUER A， UGBOLUE S C， WARNER S B. Electrospinning and properties of some nanofibers[J]. Textile Research Journal，2001，71（4）：323-328.

[13] AUDREY F， IOANNIS S. CHRONAKIS. Polymer nanofibers assembled by electrospinning[J]. Current Opinion in Colloid & Interface Science， 2004，8（1）：64-75.

[14] BAUMGARTEN P K. Electrostatic spinning of acrylic microfibers [J]. Journal of Colloid & Interface Science， 1971，36（1）：71-79.

[15] SALVETAT J-P， BRIGGS G A D， BONARD J-M， et al. Elastic and shear moduli of single-walled carbon nanotube ropes[J]. Physical Review Letters， 1999，82（5）：944-947..

[16] SALVETAT J-P， KULIK A J， BONARD J-M， et al. Elastic modulus of ordered and disordered multiwalled carbon nanotubes[J]. Advanced Materials， 1999，11（2）：161-165.

[17] BELLAN L M， KAMEOKA J， CRAIGHEAD H G. Measurement of the Youngs moduli of individual polyethylene oxide and glass nanofibres[J]. Nanotechnology， 2005，16：1095-1099.

[18] BAZBOUZ M B， STYLIOS G K. The tensile properties of electrospun nylon 6 single nanofibers [J]. Journal of Polymer Science Part B： Polymer Physics， 2010，48（15）：1719-1731.

[19] TAN E P S， GOH C N， SOW C H， et al. Tensile test of a single nanofiber using an atomic force microscope tip [J]. Applied Physics Letters， 2005，86（7）：9-15.

[20] TAN E P S， LIM C T. Physical properties of a single polymeric nanofiber [J]. Applied Physics Letters， 2004，84（9）：1603-1605.

[21] CHYASNAVICHYUS M， YOUNG S L， TSUKRUK V V. Probing of polymer surfaces in the viscoelastic regime [J]. Langmuir，2014，30（35）：10566-10582.

[22] GE S， PU Y， ZHANG W， et al. Shear modulation force microscopy study of near surface glass transition temperatures [J]. Physical Review Letters， 2000，85（11）：2340-2343.

[23] NARAGHI M， ARSHAD S N， CHASIOTIS I. Molecular orientation and mechanical property size effects in electrospun polyacrylonitrile nanofibers[J]. Polymer， 2011，52（7）：1612-1618.

[24] 左彪，劉悦，常帅锋，等.成膜因素控制的SIS膜表面环境响应行为[J].中国科学（化学），2017，47（10）：1208-1217.

[25] 赵玉荣，陈天宇，左彪，等.分子水平研究不同嵌段结构苯乙烯/丁二烯共聚物的表面结构[J].中国科学（化学），2010，40（8）：1025-1034.

[26] GE S， PU Y， ZHANG W， et al. Shear modulation force microscopy study of near surface glass transition temperatures [J]. Physical Review Letters， 2000，85（11）：2340-2343.

[27] LIUY， CHEN S， ZUSSMAN E， et al. Diameter-dependent modulus and melting behavior in electrospun semicrystalline polymer fibers[J]. Macromolecules 2011，44（11）：4439-4444.

[28] WONG S C， BAJI A， LENG S. Effect of fiber diameter on tensile properties of electrospun poly （-caprolactone） [J]. Polymer， 2008，49（21）：4713-4722.

[29] SHIN M K， KIM S I， KIM S J， et al. Size-dependent elastic modulus of single electroactive polymer nanofibers [J]. Applied Physics Letters， 2006，89（23）：231929.

[30] ARINSTEIN A， BURMAN M， GENDELMAN O， et al.Effect of supramolecular structure on polymer nanofibre elasticity [J]. Nature Nanotechnology，2007，2（1）：59-62.

[31] JI Y， LI C， WANG G， et al. Confinement-induced super strong PS/MWNT composite nanofibers [J]. Europhysics Letters， 2008，84（5）：56002.

[32] RENEKER D H， YARIN A L， ZUSSMAN E， et al. Electrospinning of nanofibers from polymer solutions and melts [J]. Advances in Applied Mechanics， 2007，41（7）：43-195.

[33] XU H. Formation and characterization of polymer jets in electrospinning [D]. Akron ：The University of Akron， 2003.

[34] KOOMBHONGSE S， LIU W， RENEKER D H. Flat polymer ribbons and other shapes by electrospinning [J]. Journal of Polymer Science Part B： Polymer Physics， 2001，39（21）：2598-2606.

[35] JARUSUWANNAPOOM T， HONGROJJANAWIWAT W， JITJAICHAM S， et al. Effect of solvents on electro-spinnability of polystyrene solutions and morphological appearance of resulting electrospun polystyrene fibers [J]. European Polymer Journal， 2005，41（3）：409-421.

[36] GUENTHNER A J， KHOMBHONGSE S， LIU W， et al. Dynamics of hollow nanofiber formation during solidification subjected to solvent evaporation [J]. Macromolecular Theory and Simulations， 2006，15（1）：87-93.

[37] STACHEWICZ U， BAILEY R J， WANG W， et al. Size dependent mechanical properties of electrospun polymer fibers from a composite structure [J]. Polymer， 2012，53（22）：5132-5137.

[38] ARINSTEIN A. Confinement mechanism of electrospun polymer nanofiber reinforcement [J]. Journal of Polymer Science Part B： Polymer Physics， 2013，51（9）：756-763.