初中数学一线三等角模型的渗透和应用

肖真

摘  要：几何困难，困难基本在于对含有复杂图形的问题，学生找不到思路，没有方向。复杂图形实际上都是由简单图形组合而成，只要我们掌握了一些常见的基本图形的解题方法，就可以把复杂图形分解为基本图形来解决。因此“基本图形分析法”是几何证明的一种重要手段。一线三等角是初中数学重要的基本图形（数学模型），也是中考常考的考点。熟悉一线三等角模型，可以快速找到解题的突破口，破解难点，使部分几何问题迎刃而解。

关键词：基本图形;一线三等角;模型

一线三等角是初中几何的基本模型，复杂图形中要学会识别基本图形，用基本图形分析法进行解题，在学习过程中注意观察积累，注重归类。

一、一線三等角基本图形及其性质

二、基本图形的渗透和应用

阶段一：学生在初二学习三角形全等，会开始接触到一线三等角证明全等三角形的题。这时候教师可以由易到难，从一线三直角的题再到普通的一线三等角，让学生感受这一类题证三角形全等，归纳出一线三等角模型。注意提示学生基本图形的结论不能直接利用，还需要证明，因为它不是教材中的公理、定理。熟悉基本图形是为了根据基本图形，想到题目的解题思路，这时只要把和基本图形相关的结论证明一下，解题的过程才算完整。

阶段二：初三时在三角形全等的基础上学习三角形相似，一线三等角相关题仍然高频率出现。学生发现一线三等角的功能变得更加强大，不需要有线段关系就可以直接推出三角形相似。这个时候教师只需要稍微提一下，学生都能反应并且掌握一线三等角推三角形相似。

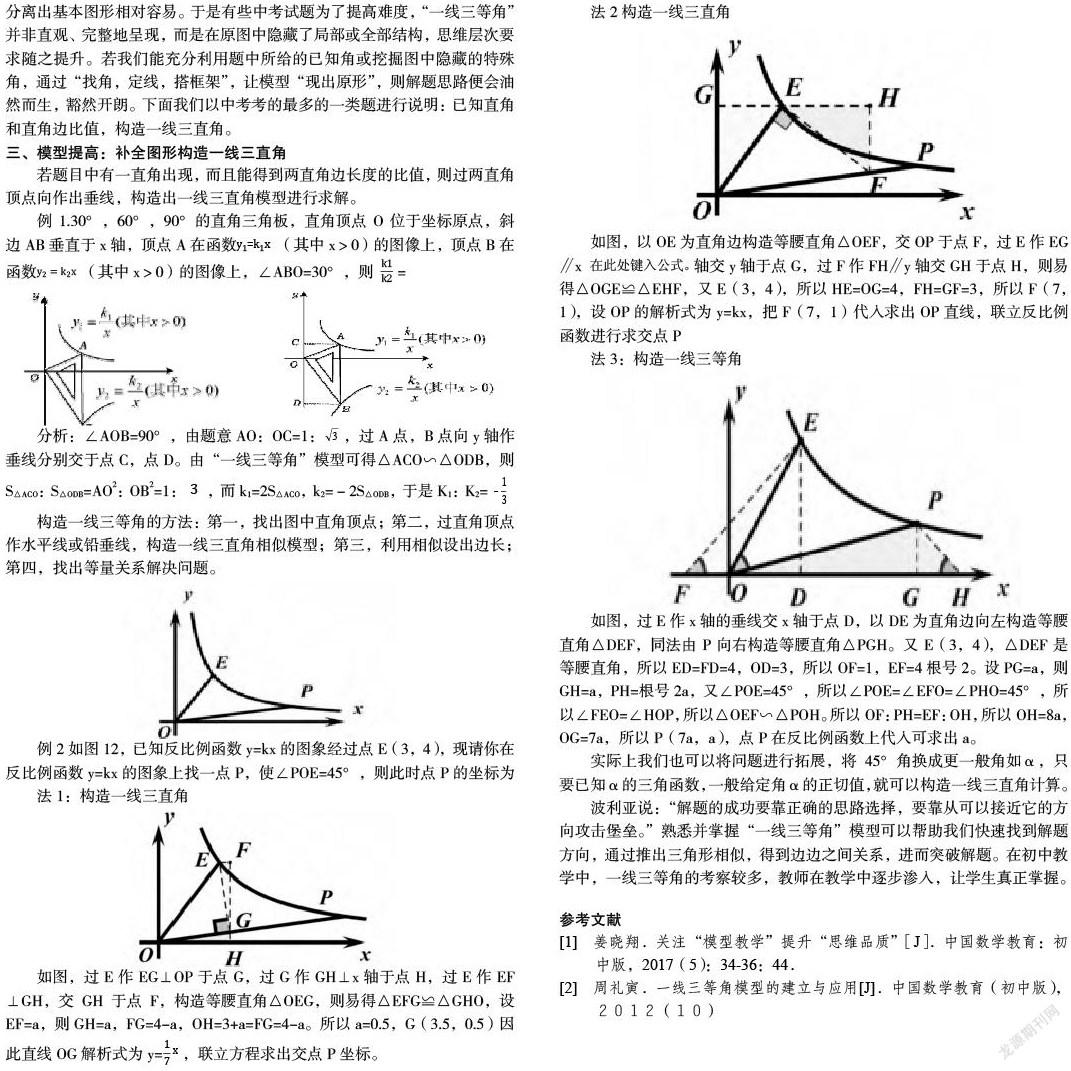
阶段三：添加辅助线构造“一线三等角”基本图形。从几何图形中直接分离出基本图形相对容易。于是有些中考试题为了提高难度，“一线三等角”并非直观、完整地呈现，而是在原图中隐藏了局部或全部结构，思维层次要求随之提升。若我们能充分利用题中所给的已知角或挖掘图中隐藏的特殊角，通过“找角，定线，搭框架”，让模型“现出原形”，则解题思路便会油然而生，豁然开朗。下面我们以中考考的最多的一类题进行说明：已知直角和直角边比值，构造一线三直角。

三、模型提高：补全图形构造一线三直角

波利亚说：“解题的成功要靠正确的思路选择，要靠从可以接近它的方向攻击堡垒。”熟悉并掌握“一线三等角”模型可以帮助我们快速找到解题方向，通过推出三角形相似，得到边边之间关系，进而突破解题。在初中教学中，一线三等角的考察较多，教师在教学中逐步渗入，让学生真正掌握。

参考文献

[1]  姜晓翔.关注“模型教学”提升“思维品质”[J].中国数学教育：初中版，2017（5）：34-36：44.

[2]  周礼寅.一线三等角模型的建立与应用[J].中国数学教育（初中版），2012（10）